|| 必ず測度を定義できる関数のこと
要するに普通の関数のこと
スポンサーリンク
目次
可測関数「普通の関数の厳密な定義」
可測関数の条件「定義域と像が可測集合」
可測関数の実数上での条件「区間内にある感じ」
可測関数の具体例「連続関数とか定義関数とか」
連続関数は可測関数
定義関数は可測関数
可測関数の性質「いろいろやっても可測関数」
可測関数の定数倍は可測関数
可測関数同士の和は可測関数
可測関数同士の積は可測関数
可測関数の冪乗は可測関数
可測関数の合成関数は可測関数
可測関数の列の上限下限も可測関数
厳密に理解したいなら
\begin{array}{llllll} \displaystyle μ^*(A∪B)&=&μ(A)+μ(B) \end{array}
この辺りを知っておく必要がありますが
かなり込み入ってるので
簡単に理解したいのであれば
この辺りの話はスルーしながら読み進めてください。
可測関数 Measurable Function
|| 可測空間の構造が破綻しない関数
可測空間同士を繋ぐ関数のこと
\begin{array}{llllll} \displaystyle (X,σ_X)&→&(Y,σ_Y) \end{array}
\begin{array}{llllll} \displaystyle f&:&X&\to&Y \end{array}
\begin{array}{cclllllll} D_Y&∈&σ_Y &&\to&& f^{-1}(D_Y)&∈&σ_X \end{array}
まあ要は「普通の関数」のことで
\begin{array}{llllll} \displaystyle f(x)&=&x && x∈D_X∈σ_X \\ \\ f(x)&=&2x && x∈D_X∈σ_X \\ \\ f(x)&=&\sin x && x∈D_X∈σ_X \\ \\ f(x)&=&e^x && x∈D_X∈σ_X \end{array}
ほぼ全ての関数は可測関数になります。
補足しておくと
X,Y の中身にはだいたい実数 R,R^2 が来ます。
(その場合はボレル集合族上で定義される)
可測関数の条件
可測空間まわりの話はちょっと面倒ですが
こいつの定義自体はすごく単純です。
\begin{array}{llllll} \displaystyle D_Y&∈&σ_Y &&\to&& f^{-1}(D_Y)&∈&σ_X \end{array}
というのも、ちょっと記号があれですが
これは要は「両側が可測集合」ってことなので
定義自体はほんとにそのまま
\begin{array}{ccccccl} \displaystyle σ_X && σ_Y \\ \\ f^{-1}(D_Y) &←&D_Y \\ \\ f^{-1}(y) &←&y \end{array}
ちょっと迂遠な言い回しかもしれませんが
特に変な条件ではありません。
単純な疑問
これはどうしてか
逆関数 f^{-1}:X←Y で定義されてますが
\begin{array}{ccccccccccccccl} \displaystyle D_X∈σ_X &&\to&& f(D_X)∈σ_Y \\ \\ x∈D_X &&\to&& f(x)∈D_Y \end{array}
別にこれでもよくない?ってなりますよね。
\begin{array}{cccllllll} \displaystyle x&∈&D_X&∈&σ_X \\ \\ f(x)&∈&f(D_X)&∈&σ_Y \end{array}
これはこれで
D_X,f(D_X) は両方とも可測集合ですし。
なぜ逆関数なのか
これは主に
「逆関数の性質」の良さと
(全単射として定義される点が良い)
\begin{array}{ccccccccccc} \displaystyle f(X ∪ A)&=&f(X) ∪ f(A) \\ \\ f^{-1}(Y ∪ B)&=&f^{-1}(Y) ∪ f^{-1}(B) \\ \\ \\ \displaystyle f(X ∩ A)&\textcolor{skyblue}{⊂}&f(X) ∩ f(A) \\ \\ f^{-1}(Y ∩ B)&\textcolor{pink}{=}&f^{-1}(Y) ∩ f^{-1}(B) \end{array}
\begin{array}{ccccccccccccc} f(X)\setminus f(A) &\textcolor{skyblue}{⊂}&f(X\setminus A) \\ \\ f^{-1}(Y)\setminus f^{-1}(B) &\textcolor{pink}{=}& \displaystyle f^{-1}(Y\setminus B) \end{array}
「操作」的な話が理由になっていて
\begin{array}{llllll} \displaystyle f(x)&=&\displaystyle \log x \end{array}
例えばこういった関数の可測性を確認する時
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
この集合があらゆる c で可測集合になる
みたいな条件をよく使うんですが
\begin{array}{cccccllll} \displaystyle e^c&=&e^{\log x} \\ \\ e^c&=&x \end{array}
\begin{array}{llllll} \displaystyle c≤\log x &&\to&& e^c≤x \end{array}
これについて確認するためには
このように「逆関数」を求める必要があって
\begin{array}{llllll} \displaystyle I&=&(-\infty,\infty) \end{array}
\begin{array}{llllll} \displaystyle \{ x∈I \mid c≤\log x \}&=&\{ x∈I \mid e^c≤x \} \\ \\ &=&[e^c,\infty) \end{array}
「区間は可測集合である」ことから
\begin{array}{ccccccccccccccc} \displaystyle D_Y&∈&σ_Y &&\to&& f^{-1}(D_Y)&∈&σ_X \\ \\ \\ [c,\infty)&∈&σ_Y &&\to&& [e^c,\infty)&∈&σ_X \\ \\ [c,\infty)&∈&σ_Y &&\to&& f^{-1}([c,\infty))&∈&σ_X \end{array}
こんな感じの流れで
可測性は「逆関数」から確認されます。
これは他の関数を調べる場合も同様で
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
これが「可測集合」であることを調べる際には
だいたい「逆関数」を求めることになります。
(一方向だけじゃなく双方向を調べるので)
可測集合を意識した条件
「可測空間 (X,σ_X) 」が定まっているなら
「完全加法族である σ_X の要素」は
「可測集合 A 」でなければなりません。
\begin{array}{llllll} \displaystyle R&=&\{ x \mid -\infty<x<\infty \} \\ \\ &=&(-\infty,\infty) \\ \\ \\ \displaystyle R^+&=&R∪\{-\infty,\infty\} \\ \\ &=&[-\infty,\infty] \end{array}
\begin{array}{llllll} \displaystyle f&:&A&\to&R^+ \end{array}
この事実から
「可測集合 A 上の話」として
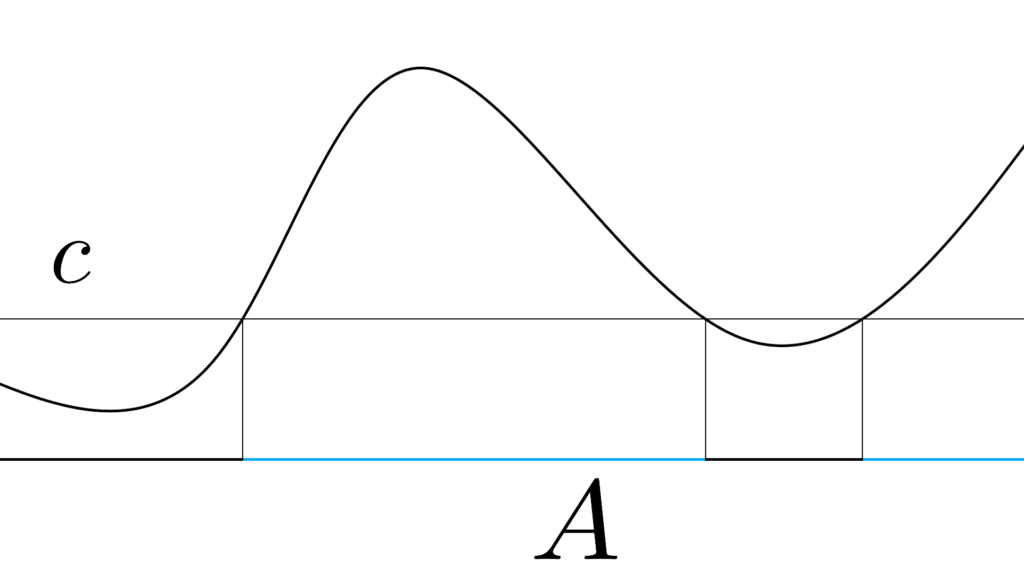
\begin{array}{llllll} D_X&=&\displaystyle \{ x∈A \mid c≤f(x) \} \\ \\ &=& f^{-1}\Bigl( [c,\infty] \Bigr) \end{array}
あらゆる値 c∈R で
f^{-1}\Bigl( [c,\infty] \Bigr) が「可測集合 D_X∈σ_X 」である
\begin{array}{cccccccll} \displaystyle A &&[c,\infty] \\ \\ f^{-1}\Bigl( f(x) \Bigr)∈σ_X &←& f(x)∈σ_Y \end{array}
始めに紹介した条件を
\begin{array}{llllll} \displaystyle (Y,σ_Y)&&\to&&\begin{array}{llll} \displaystyle (R,\mathrm{Borel}(R)) \\ \\ (R,\mathfrak{B}(R)) \\ \\ (\mathbb{R},\mathfrak{B}(\mathbb{R})) \\ \\ (\mathbb{R},\mathcal{B}(\mathbb{R})) \\ \\ (\mathbb{R},σ(O(\mathbb{R}) ) ) \end{array} \end{array}
可測だと分かってる R,R^+ で言い換えたこれが
関数 f が「可測関数である」ための
最低限の条件として扱われることがあります。
(こっちの方がよく使う)
補足しておくと
c<f(x) のとり方については
\begin{array}{llllll} \displaystyle \{ x∈A \mid f(x)≤c \} &=& f^{-1}\Bigl( [-\infty,c] \Bigr) \\ \\ \displaystyle \{ x∈A \mid f(x)<c \} &=& f^{-1}\Bigl( [-\infty,c) \Bigr) \\ \\ \displaystyle \{ x∈A \mid c<f(x) \} &=& f^{-1}\Bigl( (c,\infty] \Bigr) \end{array}
つまりこの集合が「可測である」以上
\begin{array}{llllll} \displaystyle \{ x∈A \mid f(x)≤c \}^c &=&\{ x∈A \mid c<f(x) \} \end{array}
「可測集合の補集合もまた可測集合」なので
どのようにとってもOKです。
可測関数であると同値?
A が可測集合であること
\begin{array}{ccccccccccll} &&(A,σ_A)&&(R^+,\mathfrak{B}(R^+)) \\ \\ \displaystyle f&:&A&\to&R^+ \end{array}
関数 f がこうであること
この前提のもと
「 f が可測関数である」こと
\begin{array}{cccccclcccll} \displaystyle D_Y&∈&σ_Y &&\to&& f^{-1}(D_Y)&∈&σ_X \\ \\ I&∈&\mathfrak{B}(R^+) &&\to&& f^{-1}(I)&∈&σ_A \end{array}
全ての c で
\begin{array}{llllll} f^{-1}\Bigl( [c,\infty] \Bigr)&=& \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
これが「可測集合になる」こと
これらが同値であることを
念のため確認しておきます。
可測関数である → この条件
まず以下が正しいことを前提として
\begin{array}{llllll} \displaystyle I&∈&\mathfrak{B}(R^+) &&\to&& f^{-1}(I)&∈&σ_A \end{array}
集合 I について
\begin{array}{llllll} \displaystyle I&=&[c,\infty] \end{array}
任意にとれる値 c を使って
このように定めてみると
\begin{array}{llllll} f^{-1}\Bigl( [c,\infty] \Bigr)&=& \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
逆関数の中身はこうで
\begin{array}{llllll} \displaystyle I&∈&\mathfrak{B}(R^+) &&\to&& f^{-1}(I)&∈&σ_A \end{array}
\begin{array}{ccclll} f^{-1}(I)&∈&σ_A \\ \\ \displaystyle \{ x∈A \mid c≤f(x) \}&∈&σ_A \end{array}
これは前提より
「可測集合」になりますから
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x) \}&∈&σ_A \end{array}
任意の c でこれが可測集合になる以上
『可測集合である → 実数での条件』
これは成立すると言えます。
この条件 → f は可測関数である
↑ の話とは逆に
\begin{array}{llllll} f^{-1}\Bigl( [c,\infty] \Bigr)&=& \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
今度は
任意の c でこれが可測集合になる
\begin{array}{llllll} \displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \end{array}
この条件を前提に考えてみます。
すると
\begin{array}{llllll} \displaystyle [c,\infty]&∈&\mathfrak{B}(R^+) \end{array}
これは単なる事実で
\begin{array}{cllllll} \mathrm{True} &&\to&&\displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \\ \\ [c,\infty]∈\mathfrak{B}(R^+) &&\to&&\displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \end{array}
明らかにこれは成立しますから
\begin{array}{cccccccccc}[c,\infty]&∈&\mathfrak{B}(R^+) &&\to&&\displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \\ \\ \displaystyle I&∈&\mathfrak{B}(R^+) &&\to&& f^{-1}(I)&∈&σ_A \end{array}
すぐにこれが事実として導かれ
\begin{array}{llllll} \displaystyle f&:&A&\to&R^+ \end{array}
f の定義より
\begin{array}{llllll} f^{-1}\Bigl( [c,\infty] \Bigr)&=& \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
f^{-1}(Y) の Y は
[c,\infty] の形に限定されてますから
\begin{array}{llllll} \displaystyle [c,\infty]&∈&\mathfrak{B}(R^+) &&\to&&\displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \end{array}
f は間違いなく可測関数だと言えるため
『実数での条件 → 可測集合である』
これもまた成立すると言えます。
他の範囲のとり方
↑ は以下の場合でも
\begin{array}{llllll} \displaystyle \{ x∈A \mid c<f(x) \} \\ \\ \displaystyle \{ x∈A \mid f(x)<c \} \\ \\ \displaystyle \{ x∈A \mid f(x)≤c \} \end{array}
同様の手順を辿ることができますから
全て「可測関数である」ことの条件になります。
非可測関数の例
「非可測な関数」を作るのは
「ルベーグ非可測な集合」を前提とすれば
\begin{array}{llllll} \displaystyle 1_V(x)&=&\displaystyle \left\{ \begin{array}{llllll} \displaystyle 1&&x∈V \\ \\ 0&&x∉V \end{array} \right. \end{array}
簡単に生成できます。
(ヴィタリ集合は別記事)
可測関数の具体例
可測空間 (X,σ_X),(Y,σ_Y) 上の話とすると
ほぼ全ての関数は可測関数になります。
(より正確にはそうでなければなりません)
\begin{array}{llllll} \displaystyle f(x)&=&ax+b \\ \\ f(x)&=&ax^2 \\ \\ f(x)&=&\sin x \end{array}
\begin{array}{llllll} \displaystyle 1_A(x)&=&\displaystyle \left\{ \begin{array}{clllll} \displaystyle 1 &&x \in A \\ \\ 0 &&x \not\in A \end{array} \right. \end{array}
具体的にはこれらは可測関数で
これらの足し算やら掛け算やら
合成関数やら逆関数も可測関数になります。
(こっちもそうじゃないといけません)
連続関数は可測関数
「連続関数」は「区間→区間」の関数で
\begin{array}{llllll} \displaystyle 2x&:&1&\to&2 \\ \\ \displaystyle \frac{1}{2}x&:&1&←&2 \end{array}
「逆関数」はただ逆を辿るだけなので
直感的にはもちろん可測関数です。
(というか可測関数であるべきです)
連続関数ならなんでも可測関数?
定義からちゃんとそうなるのか
きちんと確認するために定義を確認しておきます。
\begin{array}{llllll} \displaystyle \lim_{x\to c}f(x)&=&f(c) \end{array}
\begin{array}{llllll} \displaystyle |x-c|<δ&&⇒&&|f(x)-f(c)|<ε \end{array}
まず「連続関数」ですが
これは「全ての c で連続である関数」のことで
「定義域」の中では
どの点も「繋がっている」状態にあります。
これで分かると思うんですが
\begin{array}{llllll} \displaystyle f&:&A&\to&R^+ \end{array}
関数がこのように定義できるなら
\begin{array}{llllll} \displaystyle c&≤&f(x) &&\to&&[c,\infty] \end{array}
関数はこの範囲の値をとる上に
\begin{array}{llllll} f^{-1}\Bigl( [c,\infty] \Bigr)&=& \displaystyle \{ x∈A \mid c≤f(x) \} \end{array}
任意の c でこれが成立するので
これはこのようになります。
開集合と閉集合と連続
これを厳密に示すには
ただこの辺りは長くなりすぎるので
省略して結果だけ紹介すると
\begin{array}{llllll} \displaystyle |x-c|<δ &\to& |f(x)-f(c)|<ε \end{array}
「位相空間」上では
\begin{array}{llllll} \displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&←&[c,\infty] \end{array}
\begin{array}{llllll} \displaystyle (X,O_X)&\to&(Y,O_Y) \end{array}
「連続写像(関数)」は
\begin{array}{llllll} \displaystyle f^{-1}(V)∈O_X &&←&& V∈O_Y \end{array}
「開集合 ← 開集合」(開区間 ← 開区間)
「閉集合 ← 閉集合」になる(詳細は別記事)
という形で定義されているので
\begin{array}{llllll} \displaystyle O&∈&σ \end{array}
「開集合・閉集合が可測である」ことから
\begin{array}{llllll} \displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&∈&σ_A \end{array}
逆像 f^{-1}([c,\infty]) もまた可測になるため
「連続関数」は「可測である」と言えます。
(直感的には (0,1)←(0,2) こんな感じ)
定義関数は可測関数
定義関数については
\begin{array}{ccccllll} A&⊂&X \\ \\ \displaystyle A&∈&σ_X \end{array}
「逆関数の定義域が 0 か 1 」であること
\begin{array}{llllll} \displaystyle 1_A(x)&=&\displaystyle \left\{ \begin{array}{clllll} \displaystyle 1 &&x \in A \\ \\ 0 &&x \not\in A \end{array} \right. \end{array}
その考えられる出力が
以下の 4 通りしかないことから
\begin{array}{llllll} \displaystyle 1_A^{-1}(1)&→&A \\ \\ 1_A^{-1}(0)&→&A^c \end{array}
\begin{array}{llllll} ∅&∈&σ_X \\ \\ \displaystyle A&∈&σ_X \\ \\ A^c&\in&σ_X \\ \\ X&∈&σ_X \end{array}
その全ての要素が
「 σ_X の要素である」
これが確かである以上
\begin{array}{llllll} \displaystyle D_Y&=&0,1 \end{array}
\begin{array}{rcccrll} D_Y∈σ_Y &&\to&& 1_A^{-1}(D_Y)∈σ_X \\ \\ \displaystyle 0,1∈σ_Y &&\to&& ∅,A,A^c,X ∈σ_X \end{array}
改めて言うまでもなく
「定義関数 1_A(x) 」は
「可測関数」の条件を満たすと言えます。
可測関数への各操作
まず前提として
「普通の関数」は「可測でなければならない」
これが順番的には先であることを意識しておきましょう。
\begin{array}{cllllll} \displaystyle f+g \\ \\ fg \\ \\ f\circ g \\ \\ αf &&α∈R \\ \\ |f|^α &&α∈R \end{array}
その上で
「可測関数の定義として定めたこと」
\begin{array}{llllll} D_Y&∈&σ_Y &&\to&& f^{-1}(D_Y)&∈&σ_X \end{array}
\begin{array}{llllll} \displaystyle f^{-1}\Bigl( [c,\infty] \Bigr)&=&\displaystyle \{ x∈A \mid c≤f(x) \} &∈&σ_X \end{array}
これが正しいかどうか確認していきます。
使う記号の整理
ちょっと記号がややこしいので
使うやつを整理しておきます。
\begin{array}{ccccccccccc} (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \end{array}
まず可測空間はこんな感じ
\begin{array}{ccccccccccc} (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ x∈X∈σ_X && y∈Y∈σ_Y && z∈Z∈σ_z \end{array}
実数 x,y,z の所在はこんな感じで
\begin{array}{ccccccccccccccc} \displaystyle & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ f &X &\to& Y \\ \\ g& && Y &\to &Z \end{array}
関数(一意出力の写像)はこんな感じです。
また
\begin{array}{ccccccccccc} & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ f^{-1} &X &←& Y \\ \\ g^{-1}& && Y&←&Z \end{array}
逆関数 f^{-1},g^{-1} はこんな感じで
合成関数 g \circ f は
\begin{array}{ccccccccccccccc} \displaystyle & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ f &X &\to& Y \\ \\ g& && Y&\to&Z \\ \\ \\ g \circ f &X&& &\to& Z \\ \\ (g \circ f)^{-1} &X&& &←& Z \end{array}
\begin{array}{llllll} \displaystyle g \circ f(x)&=&g\Bigl( f(x) \Bigr) \end{array}
ちょっとややこしいですが
\begin{array}{llllll} \displaystyle (g \circ f)^{-1} \end{array}
経路が Z \to Y\to X であることから
\begin{array}{ccccccccccccccc} \displaystyle & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ f^{-1} &X &←& Y \\ \\ g^{-1}& && Y&←&Z \\ \\ \\ (g \circ f)^{-1} &X&& &←& Z \\ \\ f^{-1} \circ g^{-1} &X&& &←& Z \end{array}
\begin{array}{llllll} (g \circ f)^{-1}(z)&=&x \\ \\ \\ \displaystyle f^{-1} \circ g^{-1}(z) &=& f^{-1} \Bigl( g^{-1}(z) \Bigr) \\ \\ &=&f^{-1} \Bigl( y \Bigr) \\ \\ &=&x \end{array}
\begin{array}{llllll} \displaystyle (g \circ f)^{-1}(z)&=&f^{-1} \circ g^{-1} (z) \\ \\ && f^{-1} \circ g^{-1}&=&f^{-1} \Bigl( g^{-1}(z) \Bigr) \end{array}
こんな感じになっています。
合成関数の諸注意
合成関数は交換ができない
\begin{array}{llllll} \displaystyle g \circ f&≠&f \circ g \end{array}
これはちゃんと理解しておく必要があります。
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle f(x)&=&x+1 \\ \\ g(x)&=&2x+1 \end{array} &\to& \begin{array}{llllll} \displaystyle f \Bigl( g(x) \Bigr)&=&(2x+1)+1 \\ \\ \displaystyle g \Bigl(f(x) \Bigr)&=&2(x+1)+1 \end{array} \end{array}
記号としては細かく見えますが
交換をしてしまうのは明確な間違いなので
しないようにしましょう。
\begin{array}{ccccr} \displaystyle g(y)&=&z && \mathrm{Defined} \\ \\ f(z)&=& ? &&\mathrm{not} \,\, \mathrm{Defined} \end{array}
ちなみに表記としては
「出力 z するやつ g(y) が左」で
「その中身 y=f(x) が右」になります。
可測関数の定数倍は可測関数
f が可測関数である
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x) \} &∈&σ_X \end{array}
この事実から
\begin{array}{llllll} \displaystyle A_{kf}&=&\displaystyle \{ x∈A \mid c≤kf(x) \} \end{array}
\begin{array}{llllll} \displaystyle A_{kf} &\to&\begin{array}{rllllll} \displaystyle \left\{ x∈A \, \middle| \, \frac{c}{k}≤f(x) \right\}∈σ_X &&0<k \\ \\ \displaystyle \left\{ x∈A \, \middle| \, c≤0 \right\}∈σ_X &&k=0 \\ \\ \displaystyle \left\{ x∈A \, \middle| \, f(x)≤\frac{c}{k} \right\}∈σ_X &&k<0\end{array} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \left\{ x∈A \, \middle| \, c≤0 \right\} &=&\displaystyle \left\{ \begin{array}{cccclllll} \displaystyle A && c≤0 \\ \\ ∅ && 0<c \end{array} \right. \end{array}
これはすぐに導かれます。
可測関数同士の和は可測関数
f,g が可測関数である
これがゴールであることから
\begin{array}{llllll} \displaystyle A_{f+g}&=&\displaystyle \{ x∈A \mid c≤f(x)+g(x) \} \end{array}
今の時点ではよく分かりませんが
\begin{array}{llllll} \displaystyle \displaystyle \{ x∈A \mid c_1≤f(x) \}&∈&σ_X \\ \\ \displaystyle \{ x∈A \mid c_2≤g(x) \} &∈&σ_X \end{array}
\begin{array}{llllll} \displaystyle \{ x∈A \mid c_1≤f(x) \}&∪&\{ x∈A \mid c_2≤g(x) \} \\ \\ \displaystyle \{ x∈A \mid c_1≤f(x) \}&∩&\{ x∈A \mid c_2≤g(x) \} \end{array}
可測だと示したい A_{f+g} を
どうにかこんな形にすれば
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x)+g(x) \} &∈&σ_X \end{array}
「可測関数の和」の可測性
これを示すことができそうな気がします。
力技で分割する
ゴールは明確なので
\begin{array}{rllllll} \displaystyle c&≤&f(x)+g(x) \\ \\ -g(x)+c&≤&f(x) \end{array}
この関係と
\begin{array}{llllll} A∩B&=& \displaystyle \{ x \mid x∈A∧x∈B \} \\ \\ &=& \{ x \mid x∈A \}∩\{ x \mid x∈B \} \end{array}
集合の共通部分の定義
\begin{array}{llllll} (a,\infty)&=&\displaystyle \bigcup_{q∈Q} (a,q) \end{array}
そして和集合の性質から
\begin{array}{llllll} \displaystyle -g(x)+c && &≤&f(x) \\ \\ -g(x)+c &<& q&<&f(x) \end{array}
点 q で分割して
f(x),g(x) を分離してみます。
\begin{array}{llllll} A_{f+g} &=& \displaystyle \{ x∈A \mid c≤f(x)+g(x) \} \\ \\ &=&\{ x∈A \mid -g(x)+c≤f(x) \} \\ \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q \}∩\{ x∈A \mid q<f(x) \} \end{array}
するとこのような形になるので
\begin{array}{llllll} \displaystyle \{ x∈A \mid -g(x)+c<q \}&∈&σ_X \\ \\ \{ x∈A \mid q<f(x) \}&∈&σ_X \end{array}
これが可測で
\begin{array}{llllll} \displaystyle \{ x∈A \mid -g(x)+c<q \}∩\{ x∈A \mid q<f(x) \} &∈&σ_X \end{array}
この「共通部分」「和集合」
これらも「可測」になることから
\begin{array}{llllll} \displaystyle \{ x∈A \mid c≤f(x)+g(x) \}&∈&σ_X \end{array}
結果的として
これは可測関数の条件を満たすことになります。
変な式変形
以下の式変形について
\begin{array}{llllll} A_{f+g} &=&\{ x∈A \mid -g(x)+c≤f(x) \} \\ \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \end{array}
着地を考えると
\begin{array}{llllll} A∩B&=& \displaystyle \{ x \mid x∈A∧x∈B \} \\ \\ &=& \{ x \mid x∈A \}∩\{ x \mid x∈B \} \end{array}
\begin{array}{llllll} \displaystyle \{ x∈A \mid -g(x)+c<q \}∩\{ x∈A \mid q<f(x) \} &∈&σ_X \end{array}
最終的にこうなる
ここを目指している
そのことは納得できると思うんですが
\begin{array}{llllll} A_{f+g} &=&\{ x∈A \mid -g(x)+c≤f(x) \} \\ \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \end{array}
これほんと?って感じだと思うので
きちんと確認しておきます。
代わりの数と全部の数
以下の大小関係から
\begin{array}{llllll} \displaystyle -g(x)+c&≤&f(x) \end{array}
以下の関係に切り替える
\begin{array}{llllll} \displaystyle -g(x)+c<q&∧&q<f(x) \end{array}
これは関数を分離する上で必須の操作ですが
\begin{array}{llllll} \displaystyle &&\{ x∈A \mid -g(x)+c≤f(x) \} \\ \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \end{array}
ここで「和集合をとれば両者が一致する」
この部分、なんかちょっと怪しいですよね。
やってることは
\begin{array}{llllll} \displaystyle -g(x)+c&≤&f(x) &&\to && && q&<&f(x) \\ \\ \displaystyle -g(x)+c&≤&f(x) &&\to &&-g(x)+c&<&q \end{array}
\begin{array}{rllllll} \displaystyle g(x) && [c-q,\infty) \\ \\ f(x) && [q,\infty) \end{array}
「範囲を定数 q で固定する」ことと
(関数 f(x),g(x) のままでは範囲が特定できない)
\begin{array}{cllllll} \displaystyle \{ x∈A \mid -g(x)+c<q_1∧q_1<f(x) \} \\ \\ \displaystyle \{ x∈A \mid -g(x)+c<q_2∧q_2<f(x) \} \\ \\ \vdots \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \end{array}
定数 q の全域化・変数化なんですが
(関数 f,g が任意の値をとることから)
\begin{array}{ccccccclll} \displaystyle q<f(x) &&→&&\displaystyle \forall q \, q<f(x) \\ \\ [q,\infty] &&→&& [-\infty,\infty] \end{array}
ちょっと分かり辛いと思います。
\begin{array}{cllllll} (a,\infty)&=&\displaystyle \bigcup_{q∈Q} (a,q) \\ \\ (-\infty,b)&=&\displaystyle \bigcup_{q∈Q} (q,b) \end{array}
これが分かればなんとなく分かると思うんですが
\begin{array}{llllll} \displaystyle &&\{ x∈A \mid -g(x)+c≤f(x) \} \\ \\ \\ &=&\displaystyle \bigcup_{q∈Q}\{ x∈A \mid -g(x)+c<q∧q<f(x) \} \end{array}
やってることが理解できないと
これがこうなる理由は分からないかもしれません。
有理数の稠密性
↑ は「有理数が稠密である」こと
\begin{array}{llllll} \displaystyle a&<&q&<&b \end{array}
これを利用した考え方なんですが
「稠密」とかいきなり言われても
なんかよく分からないですよね。
「稠密(ちゅうみつ)」の意味は
「ぎっしり詰まってる」とか
なんかそういう感じなんですが
\begin{array}{llllll} \displaystyle a&<&q&<&b \end{array}
これだけ言われてもって感じだと思います。
稠密だから間が存在する
「稠密である」こと
\begin{array}{llllll} \displaystyle a&<&q&<&b \end{array}
これは数式的には
このような有理数 q が必ず存在する
という感じに定義されていて
以下の操作は
\begin{array}{llllll} \displaystyle -g(x)+c &&&& ≤ &&&& f(x) \\ \\ \displaystyle -g(x)+c&<&&&q&&&<&f(x) \\ \\ \displaystyle -g(x)+c&<&q&&∧&&q&<&f(x) \end{array}
「稠密である」からこそできることになります。
大小関係が以下のようになるなら
\begin{array}{llllll} \displaystyle -g(x)+c & < & f(x) \end{array}
f(x) と -g(x)+c の差をどれだけ縮めても
その間に q は必ず存在するので
可測関数同士の積は可測関数
これは関数の積の式変形から
\begin{array}{llllll} \displaystyle (a+b)^2 &=& a^2+2ab+b^2 \\ \\ (a-b)^2 &=& a^2-2ab+b^2 \end{array}
\begin{array}{llllll} \displaystyle f(x)g(x)&=&\displaystyle \frac{1}{4}\left ( \Bigl( f(x)+g(x) \Bigr)^2-\Bigl( f(x)-g(x) \Bigr)^2 \right) \end{array}
「 2 乗しても可測である」
\begin{array}{llllll} A_{f^2}&=& \displaystyle \left\{ x∈A \,\middle|\, c≤\Bigl(f(x) \Bigr)^2 \right\} \end{array}
\begin{array}{cccllllll} \displaystyle A_{f^2}&=&A &&c<0 \\ \\ A_{f^2}&=&\displaystyle \left\{ x∈A \,\middle|\, f(x)≤-\sqrt{c} ∧ \sqrt{c}≤f(x) \right\} &&0≤c \end{array}
\begin{array}{llllll} \displaystyle c≤\Bigl(f(x)\Bigr)^2&\to&f(x)≤-\sqrt{c} ∧ \sqrt{c}≤f(x) \end{array}
「可測関数の定数倍は可測である」
「可測関数の和も可測である」
これらを踏まえると
\begin{array}{llllll} \displaystyle \left\{ x∈A \,\middle|\, c≤f(x)g(x) \right\} \\ \\ \displaystyle \left\{ x∈A \, \middle| \, c≤\frac{1}{4}\left ( \Bigl( f(x)+g(x) \Bigr)^2-\Bigl( f(x)-g(x) \Bigr)^2 \right) \right\} \end{array}
f,g が可測であれば
その積 f(x)g(x) が可測であることは
すぐに確かめられます。
可測関数の絶対値の冪乗は可測関数
f が可測関数であることから
\begin{array}{llllll} \displaystyle \displaystyle \{ x∈A \mid c≤|f(x)|^α \} \end{array}
\begin{array}{rllllll} \displaystyle \left\{ x∈A \, \middle| \, c^{\frac{1}{α}}≤|f(x)| \right\}∈σ_X &&0<α \\ \\ \displaystyle \left\{ x∈A \, \middle| \, c≤1 \right\}∈σ_X &&α=0 \\ \\ \displaystyle \left\{ x∈A \, \middle| \, |f(x)|≤ c^{\frac{1}{α}} \right\}∈σ_X &&α<0 \end{array}
これもすぐに確認することができます。
指数の大小関係と
\begin{array}{cccllll} \displaystyle 2&<& |x|^{-2} \\ \\ 2&<&\displaystyle \frac{1}{|x|^{2}} \\ \\ 2|x|^{2}&<& 1 \\ \\ |x|^{2}&<&\displaystyle \frac{1}{2} \end{array}
\begin{array}{cccll} \displaystyle 2&<& |x|^{-2} \\ \\ |x|&<&2^{-\frac{1}{2}} \end{array}
集合の関係がちょっと大変ですが
\begin{array}{llllll} && && \displaystyle c^{\frac{1}{α}}&≤&|f(x)| \\ \\ f(x)&≤&\displaystyle -c^{\frac{1}{α}} && \displaystyle c^{\frac{1}{α}}&≤&f(x) \end{array}
\begin{array}{llllll} \displaystyle A_{|f|^α} &=&\displaystyle \left\{ x∈A \, \middle| \, c^{\frac{1}{α}}≤|f(x)| \right\} \\ \\ &=&\displaystyle \left\{ x∈A \, \middle| \, f(x)≤-c^{\frac{1}{α}} ∧ c^{\frac{1}{α}}≤f(x) \right\} \\ \\ &=&\displaystyle \left\{ x∈A \, \middle| \, f(x)≤-c^{\frac{1}{α}} \right\}∩\displaystyle \left\{ x∈A \, \middle| \, c^{\frac{1}{α}}≤f(x) \right\} \end{array}
この辺りが分かれば
特に疑問に思う部分は無いと思います。
可測関数の合成関数は可測関数
これは可測関数の定義から
\begin{array}{llllll} \displaystyle D_Z&∈&σ_Z &&\to&&(g \circ f)^{-1}(D_Z)&∈&σ_X \end{array}
このような形ですぐに導かれます。
\begin{array}{ccccccccccccccc} \displaystyle & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ \\ f &X &\to& Y \\ \\ g& && Y&\to&Z \\ \\ \\ g \circ f &X&& &\to& Z \\ \\ (g \circ f)^{-1} &X&& &←& Z \end{array}
というのも
f,g は前提より可測関数なので
\begin{array}{ccccccccccc} & (X,σ_X)&&(Y,σ_Y)&&(Z,σ_Z) \\ \\ f^{-1} &X &←& Y \\ \\ g^{-1}& && Y&←&Z \end{array}
当然 ↓ のようになりますから
\begin{array}{llllll} D_Z&∈&σ_Z &&\to&&g^{-1}(D_Z)&∈&σ_Y \\ \\ D_Y&∈&σ_Y &&\to&& \displaystyle f^{-1}(D_Y)&∈&σ_X \end{array}
\begin{array}{cccllllll} g^{-1}(D_Z)&∈&σ_Y&&\to&&f^{-1}\Bigl(g^{-1}(D_Z) \Bigr)&∈&σ_X \end{array}
→ の推移律
\begin{array}{llllll} \displaystyle A&\to&B&\to&C \\ \\ A && \to &&C \end{array}
つまり「三段論法」を考えると
\begin{array}{llllll} D_Z&∈&σ_Z &&\to&&g^{-1}(D_Z)&∈&σ_Y \\ \\ && && &&g^{-1}(D_Z)&∈&σ_Y &&\to&&f^{-1}\Bigl(g^{-1}(D_Z) \Bigr)&∈&σ_X \end{array}
\begin{array}{llllll} \displaystyle D_Z&∈&σ_Z &&\to&&f^{-1}\Bigl(g^{-1}(D_Z) \Bigr)&∈&σ_X \end{array}
そのまま
このような関係が得られます。
可測関数の合成関数は可測である
以上のことから
\begin{array}{llllll} \displaystyle D_Z&∈&σ_Z &&\to&&f^{-1}\Bigl(g^{-1}(D_Z) \Bigr)&∈&σ_X \end{array}
\begin{array}{llllll} \displaystyle (g \circ f)^{-1}(z)&=&f^{-1} \circ g^{-1}(z) \\ \\ &=&f^{-1} \Bigl( g^{-1}(z) \Bigr) \end{array}
こうなので
\begin{array}{llllll} \displaystyle D_Z&∈&σ_Z &&\to&&(g \circ f)^{-1}(D_Z)&∈&σ_X \end{array}
こうなりますから
「可測関数 f,g の合成関数 g\circ f 」は
「可測関数の条件」を満たしていると言えます。
可測関数の列の上限下限も可測関数
これは要は「極限」をとっても
それが「可測関数」になるって話で
なんかややこしそうなんですが
\begin{array}{llllll} \displaystyle f_1(x),f_2(x),f_3(x),...&∈&\{f_n(x)\} \end{array}
\begin{array}{llllll} \displaystyle \left\{ x∈A \, \middle| \, f_n(x)≤c \right\}&∈&σ_X \\ \\ \displaystyle \left\{ x∈A \, \middle| \, c≤f_n(x) \right\}&∈&σ_X \end{array}
可測関数の列 \{f_n(x)\} をこうだとして
\begin{array}{rllllll} \displaystyle \sup \{f_n(x)\} &=& \overline{f}(x) \\ \\ \displaystyle \inf \{f_n(x)\} &=& \underline{f}(x) \end{array}
その上限と下限をこんな感じに書くとするなら
\begin{array}{lcrllllll} \displaystyle A_{\mathrm{sup}} &=&\displaystyle \left\{ x∈A \, \middle| \, \overline{f}(x)≤c \right\} \\ \\ &=&\displaystyle \bigcap_{n=1}^{\infty}\left\{ x∈A \, \middle| \, f_n(x)≤c \right\}&∈& σ_X \\ \\ \\ \displaystyle A_{\mathrm{inf}} &=&\displaystyle \left\{ x∈A \, \middle| \, c≤\underline{f}(x) \right\} \\ \\ &=&\displaystyle \bigcap_{n=1}^{\infty}\left\{ x∈A \, \middle| \, c≤f_n(x) \right\} &∈& σ_X \end{array}
関数のとる範囲 \overline{f}(x)≤c に気を付ければ
これは意外と簡単に示すことができます。
可測関数の正成分と負成分も可測
まず正成分 f_+ 負成分 f_- ですが
\begin{array}{llllll} \displaystyle f_+(x)&=&\displaystyle\left\{ \begin{array}{clllll} \displaystyle f(x) &&0<f(x) \\ \\ 0 && f(x)≤0 \end{array} \right. \\ \\ &=&\max\{ f(x),0 \} \\ \\ \\ \displaystyle f_-(x)&=&\displaystyle\left\{ \begin{array}{clllll} \displaystyle -f(x) &&f(x)<0 \\ \\ 0 && 0≤f(x) \end{array} \right. \\ \\ &=&\max\{ -f(x),0 \} \\ \\ &=&-\min\{ f(x),0 \} \end{array}
これはこんな感じのやつで
\begin{array}{cccclll} \displaystyle f_+&&+→+ && -→0 \\ \\ f_-&&-→+ && +→0 \end{array}
こんな感じのことをやってます。
でまあ言ってしまえばそれだけなので
\begin{array}{llllll} \displaystyle A_{f_+} &=&\displaystyle \left\{ x∈A \, \middle| \, c<f_+(x) \right\} \\ \\ A_{f_-} &=&\displaystyle \left\{ x∈A \, \middle| \, c<f_-(x) \right\} \end{array}
\begin{array}{llllll} \displaystyle A_{f_+} &=& \displaystyle \left\{ \begin{array}{cllllll} \displaystyle A &&c<0 \\ \\ \left\{ x∈A \, \middle| \, c<f(x) \right\} && 0≤c \end{array} \right. \\ \\ \\ A_{f_-} &=&\displaystyle \left\{ \begin{array}{cllllll} \displaystyle A &&c<0 \\ \\ \left\{ x∈A \, \middle| \, c<-f(x) \right\} && 0≤c \end{array} \right. \end{array}
f_+,f_- が正 + であることに気を付ければ
これの可測性は簡単に確認できます。
可測関数の絶対値も可測関数
これは ↑ の事実から
\begin{array}{llllll} \displaystyle |f(x)|&=&f_+(x)+f_-(x) \end{array}
「可測関数の和」は可測ですから
すぐに可測だということが分かります。
補足しておくと
この「絶対値の可測性」から
「ルベーグ積分の近似定理」が導かれます。
