|| ある緩い条件下では絶対に最大値最小値がある
ロルの定理なんかを証明するのに必要になります。
スポンサーリンク
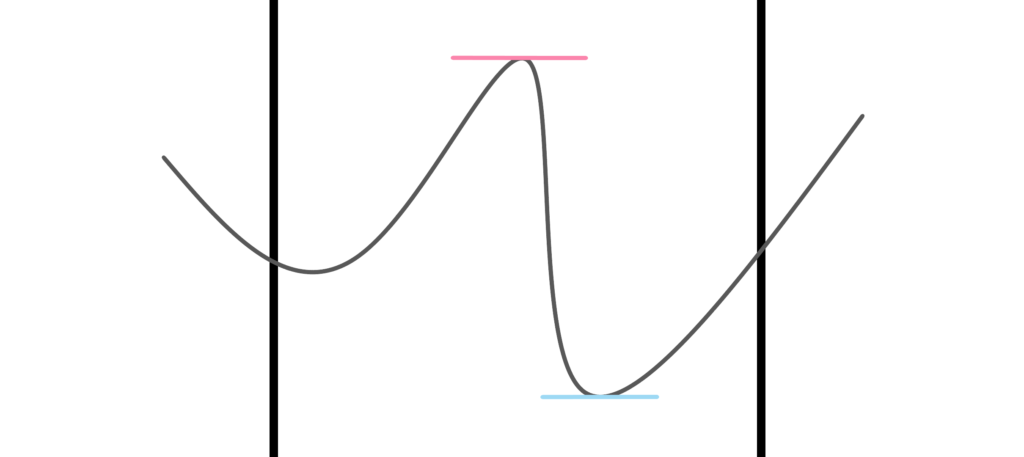
区間内にこういう線 f(x) がある時
確実に最大値や最小値が存在する。
これがこの定理の主張になります。
厳密な言い回し
f(x) が連続である
有界な閉区間 [a,b] を定義できる
この時、閉区間 [a,b] 内で f(x) は最大値最小値を持つ
補足しておくと
「閉区間」ではなく「開区間 (a,b) 」の場合
\begin{array}{llllll} \displaystyle f(x)&=&x \end{array}
このすごく単純なパターンで
最大値・最小値ともに無しとなります。
(上限 b と下限 a はあります)
有界な閉区間
「ただの閉区間」ではなく
「有界な閉区間」としているのには
ちょっと面倒な、ちゃんとした理由があります。
\begin{array}{llllll} \displaystyle (-\infty,\infty) \end{array}
というのも、実は『実数の定義』上
これもまた「ただの閉区間」なんです。
(この辺り拡大実数がどうたらの話が絡むので面倒)
\begin{array}{llllll} \displaystyle -\infty&<&m&≤&x&≤&M&<&\infty \end{array}
そしてこれは「無限」が絡むため
「有界である」状態と両立できないなど
このままではいろいろと問題が生じてしまう。
\begin{array}{llllll} \displaystyle (-\infty,\infty)&&× \\ \\ (m,\infty)&&× \\ \\ (-\infty,M)&&× \end{array}
なのでその諸問題を排除するために
ここでは「有界な閉区間」とし
「無限」を排除している
とまあそんな感じの理由があって
「有界な閉区間」としています。
補足しておくと
「実数全体」の定義は (-\infty,\infty) の範囲
「拡大実数全体」の定義が [-\infty,\infty] です。
そして「閉区間」が
『閉集合』で定義されている以上
\begin{array}{llllll} \displaystyle R&=&(-\infty,\infty) \end{array}
「実数全体」は「 -\infty,\infty を含まない」
\begin{array}{llllll} \displaystyle (-\infty,\infty) \end{array}
つまりこの区間は「境界の点を全て含む」ため
『閉区間』となります。
詳細は別の記事にまとめています。
関数が連続である
『連続』の定義は「極限」で定義されています。
\begin{array}{llllll} \displaystyle \lim_{x\to a}f(x)&=&f(a) \end{array}
関数 f(x) が x=a で連続である
これの意味は記号ではこんな感じ。
\begin{array}{llllll} \displaystyle \lim_{x\to a-0}f(x)&=&f(a)&=&\displaystyle \lim_{x\to a+0}f(x) \end{array}
より厳密には右極限と左極限で定義されています。
(右と左から近付いたら結果が一致 → 連続)
不連続である
連続ではない関数はわりと多いです。
\begin{array}{llllll} \displaystyle f(x)&=&\displaystyle\frac{1}{x} \end{array}
\begin{array}{llrlll} \displaystyle \displaystyle \lim_{x\to 0-0}\frac{1}{x}&=&-\infty \\ \\ \displaystyle \lim_{x\to 0+0}\frac{1}{x}&=&\infty \end{array}
例えばこれは 0 の点で連続ではありません。
\begin{array}{llllll} \displaystyle \lim_{x\to 0-0} \left| \frac{1}{x} \right| &=&\infty &=& \displaystyle \lim_{x\to 0+0}\left|\frac{1}{x}\right| \end{array}
同様に、このように「発散する」場合
「左右の線が平行になる」ため不連続となります。
(厳密には \infty が実数全体に含まれないため)
証明
関数 f(x) が連続である。
有界な閉区間 [a,b] を定義できる。
前提はこの2点だけですが
最大値の存在は直感的に明らか。
つまるところ
着地点さえ用意できればいいので
2つの前提から『最大値の存在』を導ければいい
\begin{array}{llllll} \displaystyle f(x)&≤&M &=&f(c) \end{array}
つまり [a,b] のどこかに
このような点 c が存在すること
あるいはそのまま M が存在することを示せば
\begin{array}{llllll} \displaystyle f(a)&=&M \\ \\ f(c)&=&M \\ \\ f(b)&=&M \end{array}
最大値の存在を証明できます。
証明に至るまでの発想
「最大値の存在」を示す。
この前段階として何を示せば良いのか。
\begin{array}{llllll} \displaystyle f(x)&≤&M \end{array}
すぐに思いつくのは
「有界である」ことを導くことだと思います。
\begin{array}{llllll} \displaystyle \inf f(x)&≤&f(x)&≤&\sup f(x) \end{array}
というのも
「上限 \sup f(x) 」は
「閉区間」であれば「最大値」と同一視できます。
\begin{array}{llllll} \displaystyle M&=&f(a)&&a&<&&&b \\ \\ M&=&f(c)&&a&<&c&<&b \\ \\ M&=&f(b)&&a&&&<&b \end{array}
つまり「有界である」ことを示せば
その性質から「上限の存在」が導かれ
そこから「最大値の存在」を導けるわけです。
有界性定理
「有界な閉区間 [a,b] 内で f(x) は連続」から
「 f(x) は有界である」を導きたい
\begin{array}{llllll} \displaystyle \inf f(x)&≤&f(x)&≤&\sup f(x) \end{array}
とまあそんなわけで
「直感的には明らかに有界である」点から
背理法を採用して考えてみます。
そのために
ここで「有界ではない」と仮定
\begin{array}{llllll} \displaystyle \lim_{x\to a}f(x)&≠&\infty \end{array}
「連続」である以上
どの a でも必ずこうなることを利用し
\begin{array}{llllll} \displaystyle \mathrm{Unbounded} &&⇒&& \displaystyle \lim_{x\to a}f(x)\textcolor{pink}{=}\infty\end{array}
仮定から矛盾を導けるよう
つまり「連続ではない」という結論が得られるよう
\begin{array}{rlclllll} \displaystyle \displaystyle \lim_{n\to \infty}f(x_n)&\textcolor{pink}{=}&\infty \\ \\ \displaystyle f(x_n)&>&n \end{array}
このような
「どこまでも大きくなる f(x_n) 」をとってみます。
(有界ではないと仮定しているためとれる)
\begin{array}{llllll} \displaystyle a&≤&x_n&≤&b \end{array}
そのために、この範囲にある
「不連続になるよう定めた点 x_n 」を考えてみると
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} x_n&=&? \end{array}
「数列 \{x_n\} 」を定義することができます。
\begin{array}{llllll} \displaystyle (-1)^n \end{array}
ただこの時点では
これが「収束する」かどうかは分かりません。
\begin{array}{llllll} \displaystyle [a,b] \end{array}
「有界な閉区間」であるため
「発散する」ことは確実にありませんが
「振動する」可能性は残っています。
\begin{array}{llllll} \displaystyle (-1)^n &&→&&(-1)^{2k} \end{array}
そこでその可能性を排除するため
つまり「収束する」ことを確定させるために
\begin{array}{llllll} \displaystyle \{x_n\}&&→&&\{x_{H(n)}\} \end{array}
\begin{array}{llcllll} \displaystyle \displaystyle \lim_{n\to\infty} x_n&=&? \\ \\ \displaystyle \lim_{n\to\infty} x_{H(n)}&=&c \end{array}
「 Bolzano-Weierstrass の定理」を使い
「収束する部分列 x_{H(n)} 」を構成
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} f(x_{H(n)})&=&\infty \end{array}
すると f(x)>n であることから
このような関係が導けるため
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty} f(x_{H(n)})&=&\displaystyle f \left( \lim_{n\to\infty}x_{H(n)} \right) \\ \\ &=&f(c) \end{array}
\begin{array}{llllll} \displaystyle f(c)&=&\infty \end{array}
f(x) が \infty になる点 c が存在する
つまり「不連続となる点 c が存在する」
ということが確定し
\begin{array}{llllll} \displaystyle \mathrm{Unbound} &&→&& f(c)=\infty \\ \\ && && \mathrm{not \,\, continuous} \end{array}
結果、仮定から矛盾が導かれる。
とまあこのようになるので
「 f(x) は有界ではない」は否定されます。
有界 → 最大値がある
「 f(x) が有界である」ことが確定したため
「上限 M の存在」もまた確定します(公理)
\begin{array}{llllll} \displaystyle f(x)&≤&M \\ \\ &&M&=&f(c) \end{array}
つまりこうなる点 c が
区間 [a,b] の中のどこかにあるはずですが
\begin{array}{llllll} \displaystyle f(c)&=&M \end{array}
まだこの時点では
この点 c が最大値と関係があるかとか
f(x) が上限値 M をとるのかとか
\begin{array}{llllll} \displaystyle f(c)&=&M &&?\\ \\ f(x)&<&M&&? \end{array}
そういったことはまだ確定していません。
\begin{array}{llllll} \displaystyle f(x)&≤&M \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}f(x_n)&=&M \end{array}
とはいえ、ゴールは見えています。
要するに「 f(c)=M の存在」を導けば良いので
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty}x_n&=&c \end{array}
\begin{array}{llllll} \displaystyle 0&≤&M-f(x)&≤&ε \\ \\ &&M-ε&≤&f(x) \end{array}
このような区間内の点 c の存在が確かなことと
その点で f(c) が M となることを導けばOK
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}x_n&=&c \\ \\ \displaystyle \lim_{n\to\infty}ε_n&=&0 \end{array}
\begin{array}{llllll} \displaystyle M-ε_n&≤&f(x_n)&≤&M \end{array}
ということは
例えばこのような形を考えれば
f(c)=M の存在を導けます。
\begin{array}{rllllll} \displaystyle \displaystyle \lim_{n\to\infty}ε_n&=&0 \\ \\ \displaystyle ε_n&=&\displaystyle\frac{1}{n} \end{array}
この部分は「 n が増えると 0 に近づく」なら
どのような形でも特に問題が無いので
分かりやすいこれを採用しておきましょうか。
\begin{array}{llllll} \displaystyle M-ε_n&≤&f(x_n)&≤&M \\ \\ \displaystyle M-\frac{1}{n}&≤&f(x_n)&≤&M \end{array}
すると
そうなるようにしたので当然ですが
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \displaystyle M-\frac{1}{n} &=&M \end{array}
「はさみうちの原理」から
n を増やせば f(x_n) が M に収束すると分かります。
そして最後
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}x_n&=&c &&? \\ \\ \displaystyle \lim_{n\to\infty}x_{H(n)}&=&c &&〇 \end{array}
有界性定理で話したように
\{x_n\} は収束するとは限らないことから
ここで「収束する部分列 \{x_{H(n)}\} 」をとり
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty}x_{H(n)}&=&c \end{array}
これが「点 c に収束する」とします。
\begin{array}{llllll} \displaystyle a&≤&x_{H(n)}&≤&b \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \lim_{n\to\infty}x_{H(n)}&=&c \end{array}
\begin{array}{llllll} \displaystyle M-\frac{1}{n}&≤&f(x_{H(n)})&≤&M \end{array}
すると前提のみで
これらは矛盾なく好きに定義できるため
ここから f(c)=M の存在が確実に。
\begin{array}{llllll} \displaystyle f(x)&≤&M \\ \\ f(c)&=&M \end{array}
結果
点 c で f(x) は上限の値をとれるので
「最大値は存在する」と言えます。
