|| 前に起きたことが後のことに影響する感じ
「複数の事象を考えた確率」のこと
前後を考える時は「複数回の試行」が前提に
スポンサーリンク
目次
条件付き確率「前に起きた上で後に起きる確率のこと」
定義「全事象が変わるだけ」
事前確率「前に起きたことの確率(条件付確率)」
事後確率「後に起きたことの確率(条件付確率)」
周辺確率「他の影響を考えなくていい確率」
同時確率「二つの事象がどちらとも起きる確率」
「前に起きたことが後に影響を及ぼす」
これは普通の感覚です。
例えば「今日やったこと」が
「明日の成果につながる」のは当然で
ここに疑問の余地はまあ無いでしょう。
で、これはもちろん確率でも同じことが言えて
例えば「コインの表が 10 連続で出た」とします。
そしたら「その後に 10 回」コインを投げれば
まあ「ほぼほぼ間違いなく 1 回は裏が出る」だろう、と
そう人間は考えますよね?
まあ要はそういう話で
「条件付き確率」はこの感覚の説明で出てきます。
条件付き確率の感覚
「前に起きたこと」と
「その後に起きたこと」の 2 つ。
これを考えた時
例えばサイコロとかコインで考えるなら
\begin{array}{llllll} \displaystyle U&=&\{1,2,3,4,5,6\} \end{array}
\begin{array}{llllll} \displaystyle \frac{1}{6}\times \frac{1}{6} \end{array}
最初に「 1 が出る」
その後に「 2 が出る」
この確率はこんな感じになります。
このパターンだと前後を入れ替えても
\begin{array}{llllll} \displaystyle \displaystyle \frac{1}{6}\times \frac{1}{6} \end{array}
こうなりますが
例えば「偶数が出る確率」は
「 2,4,6 が出る確率」なので
\begin{array}{llllll} \displaystyle \frac{1}{6}+\frac{1}{6}+\frac{1}{6}&=&\displaystyle \frac{3}{6}\end{array}
こうなって
\begin{array}{llllll} \displaystyle \frac{3}{6} && \displaystyle \frac{2}{6} \end{array}
この「偶数が出る」という『事象』は
「 2 か 4 が出る」という『事象』と
『同時』に発生することがあり得ます。
この時の「 A が起きて B が起きる」を
\begin{array}{llllll} \displaystyle A∩B \end{array}
「両方とも起きる」の言い換えとして
「共通する部分が起きる」点から
こう書くとして
\begin{array}{llllll} P(A∩B)&≠&0 \\ \\ \displaystyle P(\{2\}∩\{2,4,6\})&=&P(\{2\}) \\ \\ \\ P(A∩B)&=&0 \\ \\ \displaystyle P(\{2,4\}∩\{3,5\})&=&P(\{\}) \end{array}
このように表現することができます。
\begin{array}{llllll} \displaystyle A∩B=\{\} &&\to&& P(A∩B)=0 \end{array}
で、こういう「同時に起きない事象」だと
まあ当然こんな感じになるわけですが
\begin{array}{cccccccccc} 1,1&1,2&1,3&1,4&1,5&1,6 \\ \\ 2,1&2,2&2,3&2,4&2,5&2,6 \\ \\ &&\vdots \end{array}
「 1 回の試行では同時に起きない」けど
「複数回の試行でならどちらも起こる」
そういうパターンを考えると
\begin{array}{llllll} \displaystyle P(A \,|\, B)&=&\displaystyle \frac{|A∩B|}{|B|} \end{array}
こういうやつを考えることができる。
(記号 |A| は集合 A の要素数を意味する)
\begin{array}{llllll} \displaystyle A&=&\{(1,1)\} \\ \\ B&=&\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)\} \end{array}
「最初に 1 が出た」上で
「次に 1 が出る確率」
\begin{array}{cccllllll} \displaystyle P(A \,|\, B)&=&\displaystyle \frac{|A∩B|}{|B|} \\ \\ &=&\displaystyle \frac{1}{6} \end{array}
このような P(A \,|\, B) が
条件付き確率と呼ばれているもので
他にも「コイン」とかで考えるなら
「1回は表が出る」という事象 A と
「2回とも表が出る」という事象 B を考えた時
\begin{array}{llllll} \displaystyle U&=&\{表表,表裏,裏表,裏裏\} \\ \\ A&=&\{表表,表裏,裏表\} \\ \\ B&=&\{表表\} \end{array}
\begin{array}{llllll} \displaystyle A∩B&=&\{表表\} \end{array}
\begin{array}{cccllllll} \displaystyle P(B \,|\, A)&=&\displaystyle \frac{|A∩B|}{|A|} \\ \\ &=&\displaystyle \frac{1}{3} \end{array}
その確率はこのように表現されます。
条件付き確率の定義
定義自体は意外と直感的です。
\begin{array}{llllll} \displaystyle P(A\,|\,B)&=&\displaystyle\frac{|A∩B|}{|B|} \end{array}
全事象 U ではなく
事象 B を全体とする確率がこれで
\begin{array}{cccllllll} \displaystyle P(A)&=&\displaystyle\frac{|A|}{|U|} \\ \\ \displaystyle P(B)&=&\displaystyle\frac{|B|}{|U|} \\ \\ \displaystyle P(A∩B)&=&\displaystyle\frac{|A∩B|}{|U|} \end{array}
まあこんな感じ。
\begin{array}{cccllllll} \displaystyle \displaystyle P(A\,|\,B)&=&\displaystyle\frac{|A∩B|}{|B|} \\ \\ &=&\displaystyle\frac{\frac{|A∩B|}{|U|}}{\frac{|B|}{|U|}} \end{array}
\begin{array}{llllll} \displaystyle P(A\,|\,B)&=&\displaystyle\frac{P(A∩B)}{P(B)} \\ \\ \displaystyle P(A\,|\,B)P(B)&=&P(A∩B) \end{array}
で、これはこのような関係を持ちます。
条件付き確率の意味
事象 B が起こった上で
事象 A が起きる確率
なんて言われたりします。
\begin{array}{llllll} \displaystyle P(A\,|\,B)&=&\displaystyle\frac{|A∩B|}{|B|} \end{array}
実態は
「事象 B が起こる全ての事象の数」で
「事象 A∩B が起こる全ての事象の数」を割った数
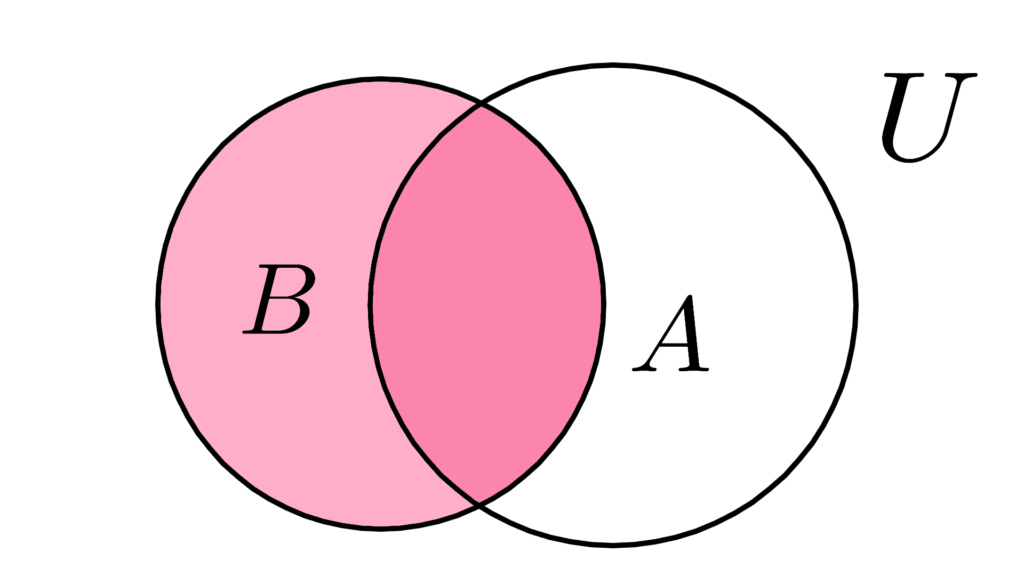
つまり「 B 上の A の割合」って感じで
B を全事象に置き換える感じになっています。
( A∩B は真ん中の濃いとこ)
事前確率 Prior Probability
|| 前の事象が起きる確率
相対的に見て「前に起きる事象の確率」のこと。
基本的に「事前と事後はセット」になります。
P(E_{\mathrm{pre}}\,|\,E_{\mathrm{af}})
記号の表現は見ての通りそのまま。
事後確率 Posterior Probability
|| 後の事象が起きる確率のこと
「事前の影響をうけるかもしれない確率」のこと。
P(E_{\mathrm{af}}\,|\,E_{\mathrm{pre}})
これもそのまま。
「事前」とセットで定められます。
ちなみに「事前」の影響を受けない時
これは単に「 P(E_{\mathrm{af}}) 」と表せます。
(この場合は事前確率も P(E_{\mathrm{pre}}) になることが)
周辺確率 Marginal Probability
|| 他の影響を受けない事象の確率
「影響を考えなくても良い確率」のこと。
まあ要は直観的で一般的な確率のことで
\begin{array}{llllll} \displaystyle P(A∩B)&=&P(A) P(B)\end{array}
「あらゆる事象 B 」と比較して
↓ のようになる事象 A
\begin{array}{llllll} \displaystyle |A∩B|&≤&1 \end{array}
『 1 元集合である』が仮定された
「基礎となる事象」の確率を
「周辺確率」と言います。
\begin{array}{ccrrrrrrrrrrr} \displaystyle & &\displaystyle \textcolor{pink}{\frac{1}{3}} & \displaystyle \textcolor{pink}{\frac{1}{2}} &\displaystyle \textcolor{pink}{\frac{1}{6}} \\ \\ \\ \displaystyle \textcolor{pink}{\frac{1}{3}} &&\displaystyle\frac{1}{3}\times\frac{1}{3} &\displaystyle\frac{1}{3}\times\frac{1}{2} &\displaystyle\frac{1}{3}\times\frac{1}{6} \\ \\ \displaystyle \textcolor{pink}{\frac{1}{2}}&&\displaystyle\frac{1}{2}\times\frac{1}{3} &\displaystyle\frac{1}{2}\times\frac{1}{2} &\displaystyle\frac{1}{2}\times\frac{1}{6} \\ \\ \displaystyle \textcolor{pink}{\frac{1}{6}}&&\displaystyle\frac{1}{6}\times\frac{1}{3} &\displaystyle\frac{1}{6}\times\frac{1}{2} &\displaystyle\frac{1}{6}\times\frac{1}{6} \end{array}
「周辺」の由来は表にすると分かると思います。
(この時の表の中にあるやつが同時確率)
ちなみに「サイコロ」とかだと
「 1 回ふって 1 が出る確率」
みたいなのが周辺確率です。
同時確率 Simultaneous Probability
|| 一緒に起きる確率
「2つの事象がどちらも起きる確率」のこと
\begin{array}{llllll} \displaystyle P(A∩B)&=&\displaystyle\frac{|A∩B|}{|U|} \end{array}
「事象 A が起きる」上で
「事象 B も起きる確率」がこれ
\begin{array}{cccllllll} \displaystyle P(\{2,4,6\}∩\{2,4\})&=&\displaystyle \frac{|\{2,4,6\}∩\{2,4\}|}{|\{1,2,3,4,5,6\}|} \\ \\ &=&\displaystyle \frac{|\{2,4\}|}{|\{1,2,3,4,5,6\}|} \\ \\ &=&\displaystyle \frac{2}{6} \\ \\ \\ \displaystyle P(\{2,4,6\}∩\{1,3,5\})&=&\displaystyle \frac{|\{2,4,6\}∩\{1,3,5\}|}{|\{1,2,3,4,5,6\}|} \\ \\ &=&\displaystyle \frac{|\{\}|}{|\{1,2,3,4,5,6\}|} \\ \\ &=&\displaystyle \frac{0}{6} \end{array}
「同時に起きない(排反)」時は当然 0 です。
前後
「試行回数」が 2 以上で考える時
「前後」という概念が登場します。
\begin{array}{llllll} P(A \,|\, B)&=&P(A) \\ \\ P(B \,|\, A)&=&P(B) \end{array}
「 1 回目で 1 が出る」
\begin{array}{llllll} \displaystyle (1,1),(1,2),(1,3),(1,4),(1,5),(1,6) \end{array}
「 2 回目で 2 が出る」
\begin{array}{llllll} \displaystyle (1,2),(2,2),(2,2),(4,2),(5,2),(6,2) \end{array}
これらの元となる事象
「 1 が出る」「 2 が出る」は
互いに影響を及ぼさないので
\begin{array}{llllll} \displaystyle \displaystyle \frac{1}{6}\times\frac{1}{6} \end{array}
同時確率はこう。
\begin{array}{llllll} \displaystyle B&=&\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)\} \\ \\ A&=&\{(1,2),(2,2),(2,2),(4,2),(5,2),(6,2)\} \end{array}
事象をこのようにしてみても
\begin{array}{llllll} \displaystyle A∩B&=&\{(1,2)\} \end{array}
\begin{array}{cccl} \displaystyle P(B)&=&\displaystyle\frac{|B|}{|U|} \\ \\ &=&\displaystyle\frac{6}{36} \\ \\ \displaystyle P(A)&=&\displaystyle\frac{|A|}{|U|} \\ \\ &=&\displaystyle\frac{6}{36} \end{array}
これはまあ当然こうなるし
\begin{array}{llllll} \displaystyle \displaystyle P(A∩B)&=&\displaystyle\frac{|A∩B|}{|U|} \\ \\ &=&\displaystyle\frac{1}{36} \end{array}
「 1 回目で 1 が出る」
その上で「 2 回目で 2 が出る確率」
というのはこのようになります。
この時
事象 A が「前」
事象 B を「後」と考えることができて
\begin{array}{cccllllll} \displaystyle P(A \,|\, B)&=&\displaystyle\frac{|A∩B|}{|B|} \\ \\ &=&\displaystyle\frac{|(1,2)|}{|{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)}|} \end{array}
\begin{array}{llllll} \displaystyle P(A∩B)&=&P(A \,|\, B)P(B) \end{array}
『 2 回目の確率』については
このように考えることができるので
\begin{array}{llllll} \displaystyle P(E_{\mathrm{pre}}∩E_{\mathrm{af}})&=&P(E_{\mathrm{af}} \,|\, E_{\mathrm{pre}})P(E_{\mathrm{pre}}) \end{array}
同時確率はこのように定めることができます。
(「試行回数 2 回」で 1 回という感じで)
以上が「条件付き確率」の感じになります。
「ベイズ統計学」の基礎となる
「ベイズの定理」なんかで出てくるので
\begin{array}{llllll} \displaystyle P(A \,|\, B)&=&P(B \,|\, A)P(A) \\ \\ P(A \,|\, B)P(B)&=&\displaystyle \frac{P(B \,|\, A)P(A)}{P(B)} \end{array}
これを理解したい場合
この「条件付き確率」は必須になります。
