|| 知ってるようでほとんど知らない
『順序』や『量』を表す概念のこと。
スポンサーリンク
「数字」は『数を表した記号』のこと
\begin{array}{cccccccccccccccccc} \displaystyle 0 & 1 & 2 & 3 & 4 & 5 & 6 & \cdots \\ \\ a&b&c&d&e \\ \\ x&y&z \end{array}
これらは『数』を意味する「記号」であり
厳密には『数』と同じものではありません。
この辺り細かいですけど
繊細なんで注意しといてください。
目次
・概要
浸透している数への印象「大きさとか量とか?」
・数の本質
自然数「人間の直観に強く結びついてるもの」
ペアノの公理「自然数の存在を公理化したもの」
・四則演算「有名な演算のこと」
加法「要するに足し算のこと( + )」
減法「まんま引き算のこと( - )」
乗算「いわゆる掛け算のこと( × )」
除算「除だけど割り算のこと( ÷ )」
演算の性質
交換律「演算を挟んで入れ替えできる」
結合律「括弧の内と外と入れ替えできる」
分配律「地味に一言で説明するのが難しい」
・自然数から作られる数
整数「自然数と引き算から生まれた数」
有理数「整数と掛け算割り算から生まれた数」
・図形の性質から得られる数
実数「実数直線なんかの図形的な性質から生まれた数」
デデキント切断「実数が満たす公理」
無理数「実数であって有理数じゃないもの」
複素数「この辺りまでくると直観から離れてくる」
というわけで
『数』について考えてみるわけですが
\begin{array}{llllll} \displaystyle \mathrm{Number} && \to && \begin{array}{llllll} \displaystyle \mathrm{Counting} \\ \\ \mathrm{Comparable} \end{array} \end{array}
まあなんとなく意味は分かると思います。
日常で「数字」を見ない
そんな人はほとんどいないでしょうし。
ただ、そもそもこいつはいったい何なのか
本当に自分は『数』のことを分かってるのか
そんなことをよくよく考えてみれば
なんかよく分からなくなると思います。
皆の知ってる数
『数』が使われている
そんな場面を思い浮かべてみてください。
すると
「時計」で時間を確認する場面とか
「買い物」なんかで金を使う場面とか
天気予報で「降水確率」を確認したりとか
ものがいくつあるか「数える」だとか
そういう場面が浮かぶと思います。
なんとなく分かる
ただそれでも
『数』っていったいなんなんだ?ってなると
なんかうまく説明できないと思います。
↑ の話はあくまで「使用例」であって
『本質』ではありませんし
「そういうもの」は「そういうもの」であって
『なんなのか』は説明できません。
でも、人は当たり前のように『数』を使えます。
手足を動かすように
空気でも吸うように
極々当たり前に人間は『数』を理解しています。
言語化してみる
「理解している」し「使える」けど
「説明できない」のが『数』
とまあ整理するとこんな感じですが
このままってのはなんか嫌ですよね。
なぜ「判断の基準」として使えるのか。
どうして「正しい」を考える時に使えるのか。
この辺り
なんとなくで済まさずに
きちんと言語化したいです。
自然数 Natural Number
|| 原点にして到達点
これは『数学の中央』にある概念になります。
\begin{array}{llllll} \displaystyle 0&1&2&3&4&5&\cdots&n&\cdots \\ \\ &1&2&3&4&5&\cdots&n&\cdots \end{array}
『数』という概念も「出発点」はこれです。
『人間の判断基準の本質』も
最終的にこれに行き着きます。
人間の直感と自然数
数学という学問は
主に『数え上げ』を基礎として発展してきました。
\begin{array}{llllll} \displaystyle 1個&2個&3個&\cdots \\ \\ 1回&2回&3回&\cdots \end{array}
『数的概念』の雛型
「人間の直観」における『量的な感覚』は
基本的にはこういった感覚からスタートしています。
比較確実性
人間の直観に近い『自然数』は
厳密には「順序数」であるとされ
\begin{array}{llllll} \displaystyle 0&≤&1&≤&2 \\ \\ 0&&&≤&2 \end{array}
『関係 ≤ 』で確実に『比較』できる
という感じに定義されています。
で、こういった性質は
そのまま『比較確実性』と言われていて
これのおかげで人は『比較』ができる。
そして『比較』ができるから
人はそこに意味を見出せる。
例えば時間なら
「時間までまだ何分かある」から「まだ大丈夫」
他にも
金銭なら「あれは何円」だから「あと何円いる」
降水確率なら「ほぼ 100\% 」なら「まず降るだろう」
とまあこんな具合に
この「比較が確実にできる」ことは
『数の本質』に近い性質だと言えます。
ペアノの公理 Peano Axioms
|| 自然数の存在を許す公理
「自然数 N 」が満たすべき最低限の要件のこと。
\begin{array}{llllll} \displaystyle \mathrm{Suc}(n)&=&n+1 \end{array}
\begin{array}{rllllll} \displaystyle 0∈N \\ \\ n∈N &&\to&&\mathrm{Suc}(n)∈N \\ \\ n∈N &&\to&&\mathrm{Suc}(n)≠0 \\ \\ n,m∈N &&\to&&n≠m\to\mathrm{Suc}(n)≠\mathrm{Suc}(m) \end{array}
\begin{array}{llllll} \displaystyle \left(\begin{array}{llllll} S⊆N \\ \\ 0∈S \\ \\ n∈N& \to &n∈S\to\mathrm{Suc}(n)∈S \end{array} \right) &\to&S=N \end{array}
形式は「帰納的定義」に近いですが
順番的にはこっちが先に来ます。
公理の内容については
大きく分けると 3 ブロック
\begin{array}{rllllll} \displaystyle 0∈N \\ \\ n∈N &&\to&&\mathrm{Suc}(n)∈N \\ \\ n∈N &&\to&&\mathrm{Suc}(n)≠0 \\ \\ n,m∈N &&\to&&n≠m\to\mathrm{Suc}(n)≠\mathrm{Suc}(m) \end{array}
\begin{array}{lllclll} \displaystyle 0∈N &&(?+1)&× \\ \\ 1∈N &&(0+1)&〇 \\ \\ 1+1∈N &&(1+1)&〇\end{array}
「初期値」「後者」と
\begin{array}{llllll} \displaystyle \left(\begin{array}{llllll} S⊆N \\ \\ 0∈S \\ \\ n∈N& \to &n∈S\to\mathrm{Suc}(n)∈S \end{array} \right) &\to&S=N \end{array}
\begin{array}{llllll} \displaystyle \begin{pmatrix} 0∈S \\ 1∈S \\ 2∈S \\ \vdots \end{pmatrix} &&\to&&S=N \end{array}
「帰納的定義の原理」で構成されてます。
( 0 とその後者を含むので必ずこうなる )
すごい当たり前のことなので
記号が分かれば意味はすぐに分かると思います。
集合論的定義
「ペアノの公理」を満たす『集合』
\begin{array}{llllll} \displaystyle 0&:=&\{\} \\ \\ \mathrm{Suc}(n)&:=&\{n\} \\ \\ \mathrm{Suc}(n)&:=&n∪\{n\} \\ \\ \mathrm{Suc}(n)&:=&2^n \end{array}
この表現方法はいくらでもあるんですが
有名なやり方だとだいたい 3 通りあって
\begin{array}{llllll} \mathrm{Suc}(n)&:=&n∪\{n\} \\ \\ \mathrm{Suc}(n)&:=&2^n \end{array}
「推移律」を満たす点から
だいたいこの辺りが採用されます。
推移律は満たしていて欲しい
これもまあ当然の話でしょう。
\begin{array}{llllll} \displaystyle 0&≤&1&≤&2&≤&3 \\ \\ 0&≤&&&&&3 \end{array}
例えば『 0 と 3 』で考えるなら
\begin{array}{llllll} \displaystyle \mathrm{Suc}(n)&=&\{n\} \end{array}
こういう定義だと
\begin{array}{llllll} \displaystyle \{\}&∈&\left\{ \{\} \right\}&∈&\left\{ \left\{ \{\} \right\} \right\}&∈&\left\{\left\{\left\{ \{\} \right\} \right\} \right\} \\ \\ &&&&\left\{ \left\{ \{\} \right\} \right\}&∈&\left\{\left\{\left\{ \{\} \right\} \right\} \right\} \\ \\ \{\}&& && &∉&\left\{\left\{\left\{ \{\} \right\} \right\} \right\} \end{array}
直接的に比較ができません。
\{\{\{\{\}\}\}\} の要素は「 \{\{\{\}\}\} だけ」ですから
他の集合との関係は不明です。
\begin{array}{llllll} \displaystyle \mathrm{Suc}(n)&=&n∪\{n\} \end{array}
でもこうなら
\begin{array}{llllll} \displaystyle n &∈& n∪\{n\} &∈& n∪\{n\} ∪ \left\{ n∪\{n\} \right\} \\ \\ n && &∈& n∪\{n\} ∪ \left\{ n∪\{n\} \right\} \end{array}
こうなるので
ちゃんと全部と比較できます。
数字の正体
初期値を『 0:=\{\} 』とし
後者を『 \mathrm{Suc}(n):=n∪\{n\} 』としてみると
「自然数」は ↓ みたいな『集合』として定義できます。
\begin{array}{lllcll} \displaystyle 0&:=& && \{\}&=&∅ \\ \\ 1&:=&\mathrm{Suc}(0)&=&0∪\{0\}&=&\{∅\} \\ \\ 2&:=&\mathrm{Suc}(1)&=&1∪\{1\}&=&\left\{ ∅,\{∅\} \right\} \\ \\ 3&:=&\mathrm{Suc}(2)&=&2∪\{2\}&=&\left\{ ∅,\{∅\} ,\left\{ ∅,\{∅\} \right\} \right\} \\ \\ &&&\vdots \end{array}
見て分かる通り
「数字」はただのラベル(名札)です。
『数』は「記号が示すもの」
その本質は『確実に比較ができる集合』で
『比較できる』から「判断の基準」として扱えます。
自然数と集合論
数学の『基礎』は「集合論」なのに
例えばなぜ「集合学」ではなく『「数」学』なのか
\begin{array}{llllll} \displaystyle \mathrm{Set} &&\to&&\mathrm{Natural} \,\,\mathrm{Number} &&× \\ \\ \mathrm{Set} &&←&&\mathrm{Natural} \,\,\mathrm{Number} &&〇 \end{array}
この理由は
『自然数』が「比較の基準になる」上に
『実現したいもの』がこの「自然数」になるからで
\begin{array}{llllll} \displaystyle \{\} \\ \\ 0,1 \end{array}
「集合論」はあくまで『実現のための手段』
『学問のそもそもの目的』ではないから
「集合学」ではなく
「数学」と呼ばれてる
とまあそんな感じで
「集合」ではなく「数」が主役になってます。
四則演算 Arithmetic
|| 基本的な演算
基本的な『 4 つの演算』のこと
\begin{array}{cccc} \displaystyle +&- \\ \\ ×,*&÷,/ \end{array}
これらは「足し算」を基準にして定義されてます。
「引き算」は『演算子 + の逆操作』
「掛け算」は『複数回の足し算』
「割り算」は『逆元での掛け算』
「足し算」は公理です。
加法 Addition
|| 演算の原点
「足し算」のこと。
\begin{array}{llllll} \displaystyle n+m \end{array}
超が付くほど基本的なことなので
特に語ることはありません。
ペアノの定義
「演算子 + 」はその「振る舞い」から
『後者』を基にして再帰的に定義されています。
\begin{array}{llllll} \displaystyle \mathrm{Suc}(n)&=&n+1&&&n∈N \\ \\ \mathrm{Suc}(n+m)&=&n+\mathrm{Suc}(m)&&&n,m∈N \end{array}
分かり切った話ですが
一応、確認しておきましょうか。
\begin{array}{lclllll} \displaystyle \mathrm{Suc}(n)&=&\mathrm{Suc}(n-1)+1 \\ \\ &=&\mathrm{Suc}(n-2)+1+1 \\ \\ &\vdots \\ \\ &=&\displaystyle \mathrm{Suc}(1)+\displaystyle\underbrace{1+1+1+1+…+1}_{n-1} \\ \\ &=&\displaystyle \mathrm{Suc}(0)+\displaystyle\underbrace{1+1+1+1+…+1}_{n} \\ \\ &=&\displaystyle\underbrace{1+1+1+1+…+1}_{n+1} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle n&=&\underbrace{1+1+1+1+…+1}_{n} \end{array}
まあ当然こう
\begin{array}{llllll} \displaystyle n+(m+1)&=&(n+m)+1 \end{array}
\begin{array}{llllll} \displaystyle \mathrm{Suc}(n+m)&=&(n+m)+1 \\ \\ &=&n+(m+1) \\ \\ &=&n+\mathrm{Suc}(m) \end{array}
演算子 + が「結合律」を満たすことから
これも当然こうなります。
まあ「足し算」ですし
分かり切ってると思うので
これらについて特に疑問はないと思います。
減法 Subtraction
|| 引き算
「加法」の逆の処理のこと。
\begin{array}{llllll} \displaystyle n-m \end{array}
「加法」が『 n+m=x の x を求める操作』なら
「減法」は『 n+x=m の x を求める操作』になります。
\begin{array}{llllll} \displaystyle x&=&m-n \end{array}
この時に定義できる『演算子 - 』が「減法」で
\begin{array}{llllll} \displaystyle 1-3&=&-2 \end{array}
「 m<n 」の時
ここで初めて「負の数」が出てきます。
逆を言えば
「演算子 + だけの世界」では
「負の数」を定義することはできません。
ただ変な話ですが
その「存在」は観測することができます。
\begin{array}{llllll} \displaystyle n+x&=&m \end{array}
「 m<n なら x は?」みたいな考え方で。
(強制法の感覚)
乗法 Multiplication
|| 掛け算
『 2 重に加法を行う操作』のこと
\begin{array}{llllll} \displaystyle m×n&=&\displaystyle\underbrace{m+m+m+\cdots+m}_{n} \\ \\ &=&\displaystyle\underbrace{\underbrace{1+1+\cdots+1}_{m}+\cdots+\underbrace{1+1+\cdots+1}_{m}}_{n} \end{array}
この状態を省略して表現するために
「乗法」は必要になります。
\begin{array}{cccccccccccccc} \textcolor{pink}{1}&2&3&4&5&6&7&8&9 \\ \\ \textcolor{gray}{2}&\textcolor{pink}{4}&6&8&10&12&14&16&18 \\ \\ \textcolor{gray}{3}&\textcolor{gray}{6}&\textcolor{pink}{9}&12&15&18&21&24&27 \\ \\ \textcolor{gray}{4}&\textcolor{gray}{8}&\textcolor{gray}{12}&\textcolor{pink}{16}&20&24&28&32&36 \\ \\ \textcolor{gray}{5}&\textcolor{gray}{10}&\textcolor{gray}{15}&\textcolor{gray}{20}&\textcolor{pink}{25}&30&35&40&45 \\ \\ \textcolor{gray}{6}&\textcolor{gray}{12}&\textcolor{gray}{18}&\textcolor{gray}{24}&\textcolor{gray}{30}&\textcolor{pink}{36}&42&48&54 \\ \\ \textcolor{gray}{7}&\textcolor{gray}{14}&\textcolor{gray}{21}&\textcolor{gray}{28}&\textcolor{gray}{35}&\textcolor{gray}{42}&\textcolor{pink}{49}&56&63 \\ \\ \textcolor{gray}{8}&\textcolor{gray}{16}&\textcolor{gray}{24}&\textcolor{gray}{32}&\textcolor{gray}{40}&\textcolor{gray}{48}&\textcolor{gray}{56}&\textcolor{pink}{64}&72 \\ \\ \textcolor{gray}{9}&\textcolor{gray}{18}&\textcolor{gray}{27}&\textcolor{gray}{36}&\textcolor{gray}{45}&\textcolor{gray}{54}&\textcolor{gray}{63}&\textcolor{gray}{72}&\textcolor{pink}{81} \end{array}
また「九九」なんかは
これを瞬時に行えるようにするためにあります。
除法 Division
|| 割り算
「乗算の逆の処理」のこと。
\begin{array}{llllll} n÷m \\ \\ \displaystyle n/m \end{array}
「掛け算」は「 m×n=x の x (積)」を求めますが
「割り算」は「 n×x=m の x (商)」を求めます。
\begin{array}{llllll} \displaystyle n\times n^{-1}&=&1 \end{array}
\begin{array}{llllll} \displaystyle n÷m&=&n\times m^{-1} \end{array}
一般的には
「乗法の逆元 n^{-1} 」で乗法の演算を行う感じです。
(有理数が発見されますが詳細は後で)
交換法則 Commutative law
集合 S に『演算 * 』が定義されていて
\begin{array}{llllll} \displaystyle a*b&=&b*a \\ \\ \\ a+b&=&b+a \\ \\ a×b&=&b×a \end{array}
↑ を満たす時
『可換である』だとか
『交換律を満たす』とか言います。
結合法則 Associative Law
集合 S に『演算 * 』が定義されてる時
\begin{array}{llllll} \displaystyle (a*b)*c&=&a*(b*c) \end{array}
↑ を満たすとき『結合律を満たす』と言います。
分配法則 Distributive Property
集合 S に『和と積の演算 +,× 』がある時
\begin{array}{llllll} \displaystyle (a+b)×c&=&ac+bc \\ \\ c×(a+b)&=&ac+bc \end{array}
↑ を満たすなら
『積は和について分配的である』と言います。
整数 Ganze Zahl
|| 0 の向こう側
『自然数』に「負の数」を導入した数のこと
\begin{array}{llllll} \displaystyle \cdots&-n&\cdots &-2&-1&0&1&2&\cdots&n&\cdots \end{array}
具体的にはこんな感じの見慣れたやつです。
\begin{array}{llllll} \displaystyle Z&=&\{n-m \mid n,m∈N\} \end{array}
『自然数 N 』と『演算子 - 』で定義されます。
有理数 Quotient
|| 定義できないやつが出てくる最初の領域
「割り算」で作れるやつを全部集めたやつ。
\begin{array}{llllll} \displaystyle Q&=&\displaystyle\left\{ \frac{n}{d} \, \middle| \, \Bigl( n,d∈Z \Bigr) ∧ \Bigl( d≠0 \Bigr) \right\} \end{array}
「分数」で表現したりします。
分数 fraction
「 / 」は『括線 Vinculum』
\begin{array}{llllll} \displaystyle \frac{n}{d} \end{array}
『 n は分子 numerator』
『 d は分母 denominator』と呼ばれます。
実数 Real Number
|| 人間の直観が働く最大の領域
『実数直線』を説明するためのもの
\begin{array}{llllll} \displaystyle R&=&\displaystyle \{x \mid -\infty <x< \infty \} \end{array}
「視覚的な数」から見出されたものですが
\begin{array}{llcllll} \displaystyle 1.4142&<&\sqrt{2}&<&1.4143 \\ \\ 3.1415&<&π&<&3.1416 \end{array}
有理数の範囲で記述することが可能です。
デデキント切断 Dedekind Cut
|| 実数直線は綺麗に分解できる
「間にある」ものと「最大・最小」を利用して
「実数の持つ連続性」を表現する方法
\begin{array}{llllll} \displaystyle 3&<&π&<&4 \\ \\ 3.1415&<&π&<&3.1416 \end{array}
例えば無理数はこういう感じなので
『実数より小さい集合(有理数など)』では
「隙間」として機能します。
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&=&\{x∈S \mid x≤a \} \\ \\ I_{\mathrm{right}}&=&\{x∈S \mid a<x \} \end{array}
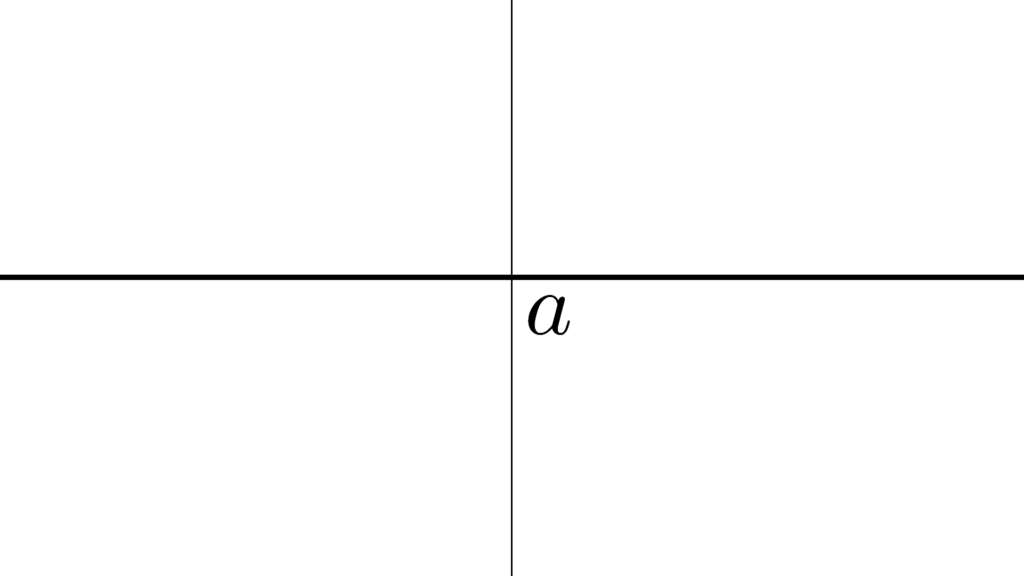
厳密にはこういう「分割・切断」があった時
「集合の組 (I_{\mathrm{left}},I_{\mathrm{right}}) 」を
「 S の切断」と言って
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}∪I_{\mathrm{right}}&=&S \\ \\ I_{\mathrm{left}}∩I_{\mathrm{right}}&=&\{\} \end{array}
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&≠&\{\} \\ \\ I_{\mathrm{right}}&≠&\{\} \end{array}
例えば以下のような「切断」を考えると
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&=&\{x∈S \mid x≤\textcolor{skyblue}{π} \} \\ \\ I_{\mathrm{right}}&=&\{x∈S \mid \textcolor{skyblue}{π}<x \} \end{array}
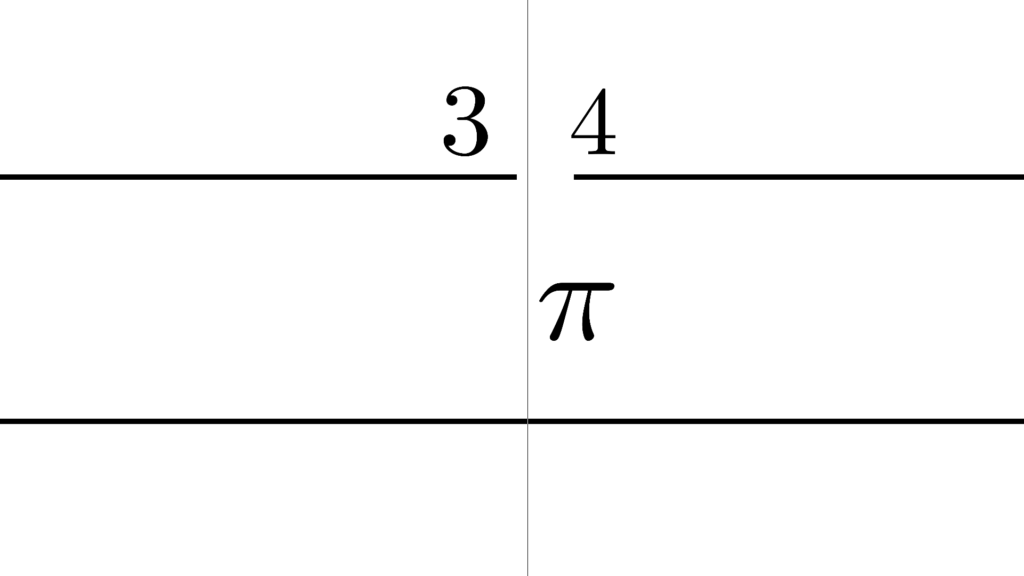
\begin{array}{cccccccccccc} && && \mathrm{max}(I_{\mathrm{left}}) &\min(I_{\mathrm{right}}) \\ \\ \displaystyle S=Z &&\to&& 〇 & 〇 \\ \\ \displaystyle S=Q &&\to&& × & × \\ \\ \displaystyle S=R &&\to&& 〇 & × \end{array}
「最小値」「最大値」の性質から
\begin{array}{cccccccccccc} \mathrm{max}(I_{\mathrm{left}}) &\min(I_{\mathrm{right}}) \\ \\ 〇 & × \end{array}
これを満たすのは
『 π などの無理数を含む』
「全体を内側に持つ」実数のパターンだけですから
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&=&\{x∈\textcolor{pink}{R} \mid x≤π \} \\ \\ I_{\mathrm{right}}&=&\{x∈\textcolor{pink}{R} \mid π<x \} \end{array}
\begin{array}{cccccccccccc} \mathrm{max}(I_{\mathrm{left}}) &\min(I_{\mathrm{right}}) \\ \\ 〇 & × \end{array}
この時の「 ↑ の切断(正常な切断)」だけが
『実数の連続性』を保証すると言えます。
整理すると
『 S が連続』←『任意の切断が正常な切断』です。
(無理数パターンで整数と有理数はアウト)
そしてこの
『任意の切断が正常な切断』→『 S が連続』が
「デデキントの公理」になります。
無理数 Irrational Number
|| 脇役っぽいくせに超大事
『有理数ではない実数』のこと
\begin{array}{llllll} \displaystyle R&\setminus&Q \end{array}
「無理」というのは
「有理数ではない」という意味です。
\begin{array}{cccllllll} \displaystyle \sqrt{2} &\log 2 \\ \\ π & e \end{array}
こういうのがあります。
\begin{array}{llllll}|Q|&<&|R\setminus Q| \end{array}
ちなみにこいつらの方が「有理数」より多いです。
複素数 Complex Number
|| 演算の仕様と数値による平面の表現
『実数を縦に拡張したもの』のこと
\begin{array}{ccccllllll} \displaystyle i&=&\sqrt{-1} \\ \\ z&=&a+bi \\ \\ |z|&=&\sqrt{a^2+b^2} \end{array}
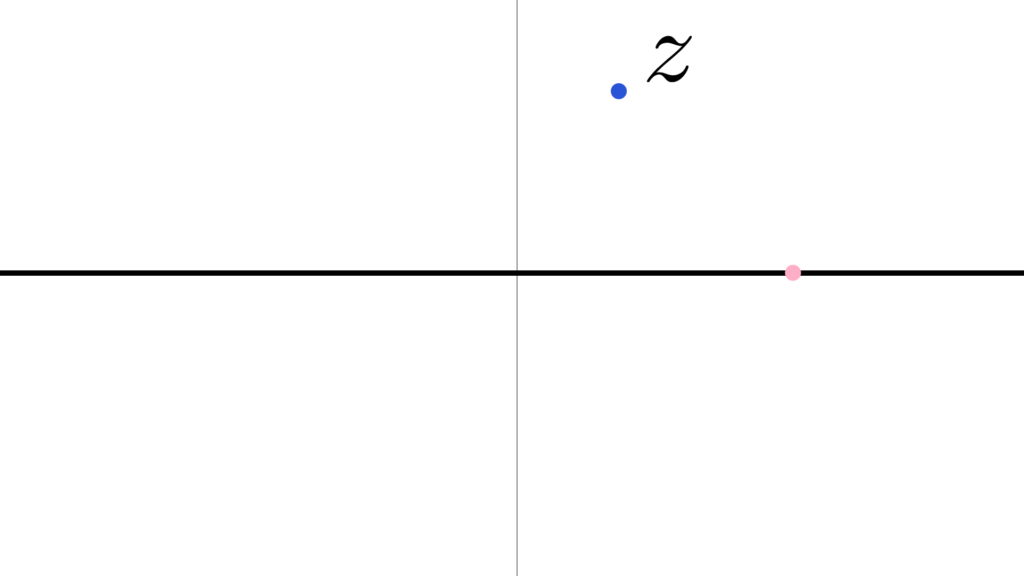
『実数』が「直線上での移動」だったのに対して
『複素数』は「平面的に移動」することを許容します。
2 乗すると普通は正
『普通(実数全体)』に考えれば
「 2 乗」するということは
\begin{array}{llllll} \displaystyle +\times + &=&+ \\ \\ -\times - &=&+ \end{array}
『正の値を得る』ということです。
\begin{array}{llllll} \displaystyle \times(-1) \end{array}
「マイナスの乗算」は
「反転」を意味する操作ですから
(減少の倍は直感的に理解できる)
「反転して反転」すれば「元通り」
\begin{array}{llllll} \displaystyle (-1) \times (-1) \end{array}
これは感覚的に分かると思います。
(演算の性質なので直感的ではありませんが)
2 乗すると負になる数
方程式で表現可能なものとして
↓ のような x が考えられるわけですが
\begin{array}{lcrlllll} \displaystyle x^2&=&-1 \\ \\ x&=&\sqrt{-1} \end{array}
これは先に示した「普通(実数)」ではありません。
\begin{array}{llllll} \displaystyle (\sqrt{-1})^2&=&-1 \end{array}
『 2 乗する』という操作で
「元通り」ではなく「反転」してしまう以上
これは直感的に捉えるのが困難です。
直感から外れる演算の性質
始まりは「乗算」と「整数」から
\begin{array}{llcllll} (-2) \times 5 &&\mathrm{Reduce} \\ \\ \displaystyle 5\times (-2) &&?\end{array}
この操作における
「 -2 倍」の意味不明さ
これがそもそもの発端で
「虚数」が直感から外れてしまう
その原因の由来となっています。
実際 -\times - =+ に関しては
\begin{array}{llllll} \displaystyle (-2)\times 3&=&(-2)×(4-1) \\ \\ &=&(-2)×4+(-2)\times (-1) \\ \\ &=&-8+(-2)\times (-1) \\ \\ &=&-6 \end{array}
\begin{array}{rcrllllll} \displaystyle -8+(-2)\times (-1) &=&-6 \\ \\ (-2)\times (-1) &=&2 \\ \\ \\ 2\times (-1)\times (-1) &=&2 \\ \\ (-1)\times (-1) &=&1 \end{array}
この「計算の整合性」から得られるため
そもそも直感的ではありません。
(数字の範囲外だと直感的 裏の裏 → 表)
いつものように演算から得られた虚数
直感からは外れてしまっていますが
「虚数」自体はそう特別なものではありません。
\begin{array}{llllll} \displaystyle x^2&=&x\times x \end{array}
「 2 乗・冪乗」という演算から
間違いなく一意に得られるもので
概念上は確かに存在しています。
\begin{array}{llllll} \displaystyle x^2&=&-1 \end{array}
それに『演算の整合性』を保証する上で
これは絶対に必要です。
虚数の意味
2 乗すると正ではなく負になる
\begin{array}{rlclllll} \displaystyle \times (-1)&&\mathrm{Reverse} \\ \\ \times \sqrt{-1} &&? \end{array}
これを分解して考えてみると
\begin{array}{llllll} \displaystyle (-1)^2 &=&+1 \\ \\ \left((\sqrt{-1})^2\right)^2 &=&+1 \end{array}
2 乗という操作は
「反転させた後にまた反転させていた」から
結果として「元通り」になっていた
\begin{array}{llllll} (-1)^2&=&\displaystyle (-1)\times (-1) \end{array}
まあつまり
「元通りにする操作」ではなく
「同じ操作を2回繰り返している」だけである。
これが改めて確認できるので
\begin{array}{llllll} \displaystyle x^2&=&-1 \end{array}
この「虚数 \sqrt{-1} 」それ自体は
「そういう操作」だということが
なんとなく分かります。
4 乗すると元に戻る
「虚数」の性質を確認してみると
\begin{array}{llllrl} \displaystyle \sqrt{-1}&=&i \\ \\ && i^0&=&1 \\ \\ && i^1&=&i \\ \\ && i^2 &=&-1 \\ \\ && i^3 &=&-i \\ \\ && i^4 &=&1 \end{array}
このようになることが分かるため
\begin{array}{lcrlllll} \displaystyle (-1)^0&=&1 \\ \\ (-1)^1&=&-1 \\ \\ (-1)^2 &=& 1 \end{array}
これをこのパターンと比較して見てみると
「虚数 i 」の具体的な位置が
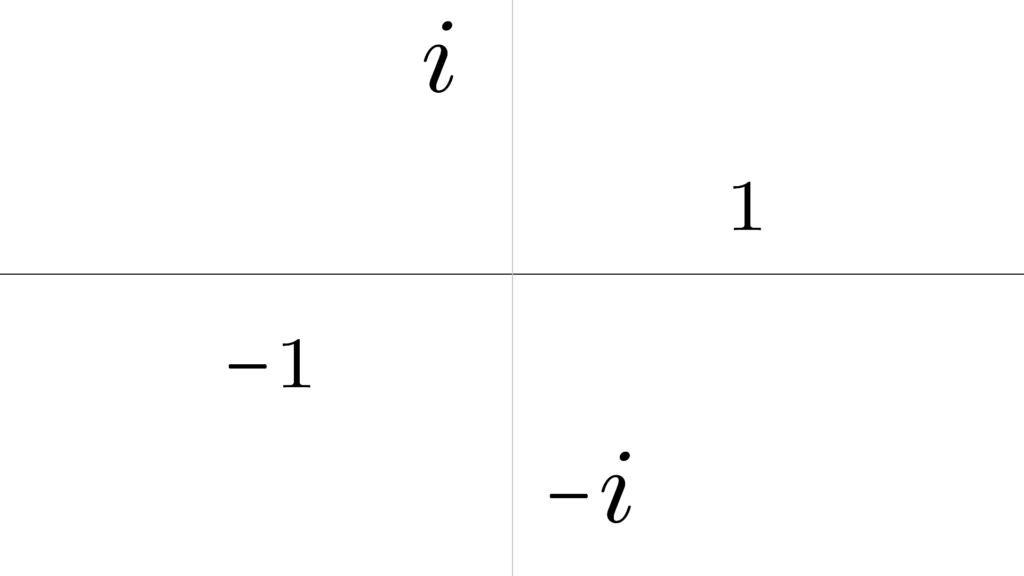
なんとなくですが見えてきます。
虚数と平面
↑ では勝手に平面で考えてしまいましたが
\begin{array}{llllll} \displaystyle ?&≤&i&≤&? \end{array}
この時点では
「虚数」が「実数直線上にあるかどうか」
これがまだ分かっていません。
\begin{array}{llcllll} \displaystyle \times (-1) &&180° \\ \\ \times \left(\sqrt{-1}\right)^2 &&180° \\ \\ \times \sqrt{-1} &&90° \end{array}
しかし振る舞いから考えると
虚数はこのような「回転」を表している
これはなんとなく分かります。
実数直線上と虚数
実数直線上に虚数が無い
これは感覚的に分かりますが
\begin{array}{llcllll} \displaystyle \times (-1) &&180° \\ \\ \times \sqrt{-1} &&90° \end{array}
一応ちゃんと確認しておくと
まず触りから行くなら
例えば a,b を『正の有理数』だとして
\begin{array}{llllll} \displaystyle a&<&i&<&b \end{array}
こうなると仮定すると
\begin{array}{cccccccccccc} \displaystyle a^2&<&i^2&<&b^2 \\ \\ a^2&<&-1&<&b^2 \end{array}
\begin{array}{cccccccccccc} \displaystyle 2^2&<&3^2&<&4^2 \\ \\ \displaystyle \left( \frac{1}{4} \right)^2&<&\displaystyle \left( \frac{1}{3} \right)^2&<&\displaystyle \left( \frac{1}{2} \right)^2 \end{array}
こうなるわけですが
\begin{array}{llllll} \displaystyle a^2&<&-1 \end{array}
この条件を満たす有理数 a は存在しません。
つまり『有理数との大小比較』の中でも
特に『下から抑える』ことは「不可能」
『上から抑える』場合にしても
\begin{array}{llllll} \displaystyle -1&<&b^2 \end{array}
b はいくらでも小さくできるので
\begin{array}{llllll} \displaystyle -1&<&0 \end{array}
こうなりますから
少なくとも『正の有理数』の範囲には無い
ということが分かります。
\begin{array}{cccccccccccc} a&<&i&<&b \\ \\ \\ \displaystyle b^2&<&i^2&<&a^2 \\ \\ b^2&<&-1&<&a^2 \end{array}
\begin{array}{cccccccccccc} \displaystyle -4&<&-3&<&-2 \\ \\ (-4)^2&>&(-3)^2&>&(-2)^2 \end{array}
じゃあ「負の有理数」ならいけるのか
同様の手順で考えてみると
\begin{array}{llllll} \displaystyle b^2&<&-1 \\ \\ && -1&<&0 \end{array}
『上から抑えられる有理数 b 』が存在しない
『下からは 0 より上』で抑えられる
という感じの
同様の結果が得られる。
ということはつまり
『全ての有理数とは比較ができない』
\begin{array}{cccccccccccc} \displaystyle R&&a<x<b &&〇 \\ \\ &&a<i<b &&× \end{array}
これが確定するので
ほぼほぼ実数直線上に無いことが分かります。
ただこれだけじゃ不安なので
「実数」の『あらゆる切断が可能』という
「公理」ベースでも考えてみましょうか。
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&=&\{x∈\textcolor{pink}{R} \mid x≤i \} \\ \\ I_{\mathrm{right}}&=&\{x∈\textcolor{pink}{R} \mid i<x \} \end{array}
そのために
『虚数が実数と同様に振る舞う』
つまり「実数の範囲にある」と仮定すると
\begin{array}{llllll} \displaystyle x≤\sqrt{2} &\to&x^2≤2&&&〇 \\ \\ \sqrt{2}<x&\to& 2<x^2 &&&〇 \end{array}
このように
「分かる形に問題なく変換できる」はず
\begin{array}{llllccc} \displaystyle x≤i &\to&x^2≤-1&&&× \\ \\ i<x&\to& -1<x^2 &&&〇 \end{array}
なんですが、これを行うと
I_{\mathrm{left}} は条件を満たすものが無いので
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&=&\{x∈\textcolor{pink}{R} \mid x≤i \} \\ \\ \\ I_{\mathrm{left}}&=&\{x∈\textcolor{pink}{R} \mid x^2≤-1∧0<x \} \\ \\ &=&\{\} \\ \\ \\ I_{\mathrm{left}}&=&\{x∈\textcolor{pink}{R} \mid x^2≤-1∧x<0 \} \\ \\ &=&\{\} \end{array}
「空集合」になることが分かります。
これを満たす「切断する点」は
\begin{array}{llllll} \displaystyle -1&<&0&≤&x^2 \\ \\ &&0&≤&x^2 \end{array}
これが片側全体を範囲に含むので
-\infty が候補として考えられますけど
こいつの 2 乗は \infty なので
\begin{array}{ccccccccclll} -\infty&=&i &&? \\ \\ \\ (-\infty)^2&&i^2 \\ \\ \displaystyle \infty&≠&-1 &&〇 \\ \\ \\ -\infty&≠&i &&〇 \end{array}
間違いなくこう。
\begin{array}{llllll} \displaystyle I_{\mathrm{left}}&\textcolor{pink}{=}&\{\} &&× \\ \\ I_{\mathrm{left}}∪I_{\mathrm{right}}&\textcolor{pink}{≠}&R &&× \end{array}
ということはつまり
そもそも「切断」が不可能である
ということが分かるため
仮に「虚数 i が実数の範囲にある」場合
『デデキントの公理』に反することになる。
だから結果として
「実数ではない」と言えてしまいます。
複素数の平面的な感覚
「虚数」は実数直線上に無い
じゃあどこにあるんだって話なんですが
\begin{array}{rrrrrrrrrrrr} \displaystyle ↙&i&↖ \\ \\ -1 & ⇆ & 1 \\ \\ ↘&-i&↗ \end{array}
解釈にはなりますが
『実数直線の奥』にある
と考えることができます。
\begin{array}{llllrl} \displaystyle \sqrt{-1}&=&i \\ \\ && i^0&=&1 \\ \\ && i^1&=&i \\ \\ && i^2 &=&-1 \\ \\ && i^3 &=&-i \\ \\ && i^4 &=&1 \end{array}
演算の性質上
「回転」していることはほぼ確実
(振舞いはそのように解釈可能)
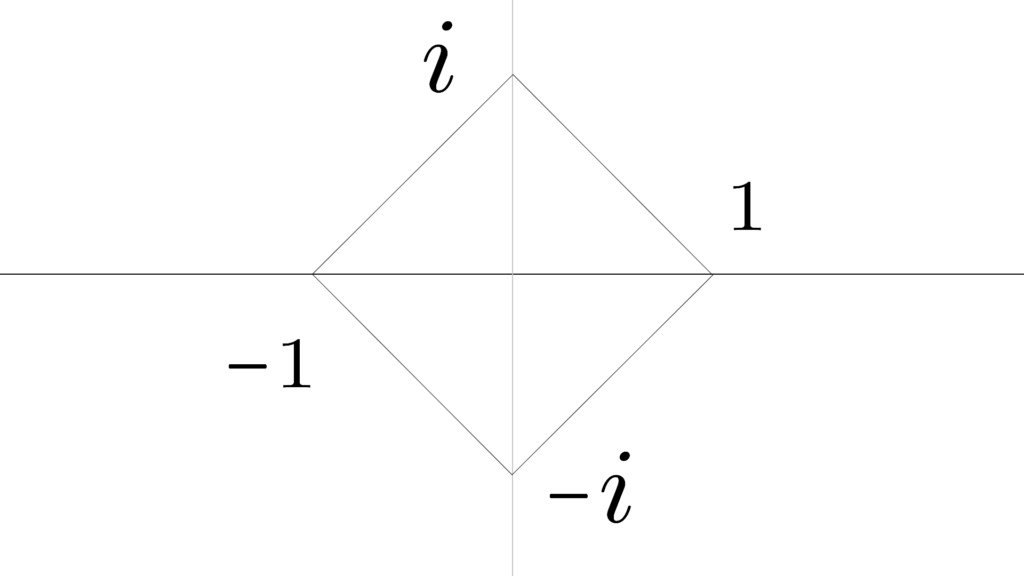
ということは
「虚数」はこんな形で存在すると解釈できます。
(極座標表示からも確認できる)
\begin{array}{llllll} \displaystyle z&=&a+bi \\ \\ &=&\displaystyle \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}+i\frac{b}{\sqrt{a^2+b^2}} \right) \\ \\ \\ &=&r(\cos θ + i\sin θ) \end{array}
そしてこの感覚が
「複素平面」の原型になります。
