|| モーメント母関数よりもっと一般的な形のやつ
モーメント母関数ではカバーしきれない
そんな複雑なものを扱うための関数のこと
スポンサーリンク
目次
特性関数「積率母関数の対応範囲を広げたやつ」
一般性の証明「特性関数だと全部行ける感じ」
マクローリン展開「いろんな関数を多項式に」
凸関数「 ∪ とか ∩ みたいな形の関数」
イェンセンの不等式「凸関数凹関数についての不等式」
「積率母関数」については当然として
「マクローリン展開」についても
先に知っておくことを推奨します。
一応ざっと説明しておくと
\begin{array}{llllll} \displaystyle M_X(t)&=&\displaystyle E\left(e^{tX}\right) \\ \\ M_X(t)&=&\displaystyle \int e^{tx}f(x) \,dx \end{array}
\begin{array}{llllll} \displaystyle \left. \frac{d^n}{dt^n}M_X(t) \right|_{t=0}&=&E(X^n) \end{array}
「積率母関数」っていうのは
「期待値・分散」なんかを出力する
良い感じに都合が良い関数のことです。
特性関数 Characteristic function
|| 積率母関数を更に一般化したやつ
積率母関数より広い範囲をカバーできる関数
\begin{array}{llllll} \displaystyle \phi_X(t)&=&\displaystyle E\left(e^{itX}\right) \\ \\ &=&\displaystyle \int e^{itx}f(x) \,dx \end{array}
\begin{array}{llllll} \displaystyle \left. (-i)^n\frac{d^n}{dt^n}\phi_X(t) \right|_{t=0}&=&E(X^n) \end{array}
期待値が計算できない場合
積分が収束しない場合など
モーメント母関数は存在しないことがあるんですけど
特性関数はその範囲の外もカバーできます。
特性関数の導出
基本的には積率母関数の発想と同様です。
「オイラーの等式」も発想に含まれますが
この辺り少し面倒なので、とりあえずスルー
\begin{array}{llllll} \displaystyle e^{iθ}&=&\cos θ+i\sin θ \end{array}
\begin{array}{llllll} \displaystyle \displaystyle e^{itx}&=&\displaystyle 1+itx+\frac{(it)^2}{2!}x^2+\frac{(it)^3}{3!}x^3+\cdots \end{array}
ともかく、これが正しいから
「結果として」このように書ける、と
まあざっくりとはそんな感じです。
基本的に、式の大まかな形は積率母関数と同様
\begin{array}{llllll} \displaystyle \displaystyle E\left(e^{itx}\right)&=&\displaystyle E\left(1\right)+E\left(itx\right)+E\left(\frac{(it)^2}{2!}x^2\right)+E\left(\frac{(it)^3}{3!}x^3\right)+\cdots \end{array}
\begin{array}{llllll} \displaystyle \frac{d}{dt} itx&=&\displaystyle ix \\ \\ \displaystyle \frac{d}{dt} (it)^2x^2&=&\displaystyle 2i^2tx^2 \\ \\ \displaystyle \frac{d}{dt} (it)^nx^n&=&\displaystyle ni^nt^{n-1}x^n \end{array}
\begin{array}{llllll} \displaystyle \left. (-i)^1\frac{d}{dt}\phi_X(t) \right|_{t=0}&=&(-i)^1i^1E(X) \\ \\ &=&E(X) \end{array}
各項には決まった次数の虚数単位が出てくるため
これを処理するためのものがついてますが
その他は特に疑問に思う部分は無いと思います。
積率母関数よりなぜ一般性があるのか
特に知識が無かったとしても
「複素数の範囲」「実数の範囲」の比較を行えば
「特性関数」が「積率母関数」より範囲が広いのは明らか。
少なくとも
「対応する数値の範囲」には明らかな差があるので
\begin{array}{llllll} \displaystyle R&⊂&C \end{array}
間違いなく積率母関数以上の一般性を備えている
これはすぐに分かると思います。
実際
「コーシー分布」など
\begin{array}{llllll} \displaystyle \frac{1}{π(1+x^2)} \end{array}
「積率母関数」は積分値が無いのに
「特性関数」には積分値がある
そういう関数がいくつかあります。
どのくらいカバーできる範囲が広がってるのか
結論だけざっくり言っておくと
こいつは「ほぼ全ての分布」をカバーできています。
\begin{array}{llllll} \displaystyle \left. (-i)^n\frac{d^n}{dt^n}\phi_X(t) \right|_{t=0}&=&E(X^n) \end{array}
詳しくやると
「留数定理」やらなんやら
積率母関数の話から逸れるので
そういった話は別記事にまとめますが
「オイラーの公式」を知っていると
\begin{array}{clllll} \displaystyle e^{iθ}&=&\cos θ+i\sin θ \\ \\ \\ |e^{iθ}|^2&=&(\cos θ+i\sin θ)\overline{(\cos θ+i\sin θ)} \\ \\ &=&(\cos θ+i\sin θ)\overline{(\cos θ+i\sin θ)} \\ \\ &=&(\cos θ+i\sin θ)(\cos θ-i\sin θ) \\ \\ &=&\cos^2θ-i^2\sin^2θ \\ \\ &=&\cos^2θ+\sin^2θ \\ \\ &=&1 \end{array}
なんか全部行けそう、みたいな
なんかそんな感じがすると思いますが
さていかがでしょうか。
代表的な特性関数
f(x) を「確率を返す関数」
\phi_X(t) を「特性関数」
M_X(t) を「積率母関数」として整理すると
\begin{array}{cccccccccc} \displaystyle & f(x) &M_X(t) &\phi_X(t) \\ \\ \\ \mathrm{N}(μ,σ^2) &\displaystyle \frac{1}{\sqrt{2πσ^2}}e^{-\frac{(x-μ)^2}{2σ^2}} &\displaystyle e^{ μt+\frac{σ^2t^2}{2} } &\displaystyle e^{μit-\frac{σ^2t^2}{2} } \\ \\ \mathrm{U}(a,b) &\displaystyle \frac{1}{b-a} & \displaystyle \frac{e^{tb}-e^{ta}}{t(b-a)} & \displaystyle \frac{e^{itb}-e^{ita}}{it(b-a)} \\ \\ \\ \mathrm{Bern}(p) &p^x(1-p)^{1-x} &(1-p)+pe^t &(1-p)+pe^{it} \\ \\ \mathrm{B}(n,p) &{}_n \mathrm{C}_{x} p^x(1-p)^{n-x} &\Bigl( (1-p)+pe^{t} \Bigr)^n&\Bigl( (1-p)+pe^{it} \Bigr)^n\\ \\ \\ \mathrm{Exp}(λ) & λe^{-λx} & \displaystyle \left( 1-\frac{t}{λ} \right)^{-1} & \displaystyle \left( 1-\frac{it}{λ} \right)^{-1} \\ \\ \\ \mathrm{Cauchy}(0,1) & \displaystyle \frac{1}{π(1+x^2)} & × & e^{0it -1|t| } \end{array}
特性関数はこんな感じになります。
(細かいところは省略してます)
特性関数の収束
ざっくりとではありますが
とりあえず証明しておきます。
ちゃんとやると本題から逸れるので
「収束」「複素数の計算ルール」
この辺りの話は省略
複素関数の収束と絶対収束
関数の収束について
考えていくと色々あるわけですが
\begin{array}{llllll} \displaystyle |f(x)| &≤&α \end{array}
「複素数」の「複素共役」から
\begin{array}{llllll} \displaystyle |z|&=&\sqrt{a^2+b^2} \end{array}
とりあえず「絶対収束」を考えてみて
\begin{array}{llllll} \displaystyle |x+y|&≤&|x|+|y| \end{array}
\begin{array}{llllll} \displaystyle \sum_{n=0}^{\infty} a_n &≤& \displaystyle\sum_{n=0}^{\infty} \left| a_n \right| \end{array}
この事実を元に
「マクローリン展開」を使い
各項に分けて考えてみると
\begin{array}{llllll} \displaystyle f(x)&=&\displaystyle 1+f^{(1)}(0)x^1+\frac{1}{2!}f^{(2)}(0)x^2 +\cdots \end{array}
\begin{array}{llllll} \displaystyle f(x) &≤& \left| f(x) \right| &≤&\displaystyle \sum_{n=0}^{\infty} \left| \frac{1}{n!}f^{(n)}(0)x^n \right| \end{array}
『関数 f(x) が収束する』ことの条件として
「絶対値の総和が収束する(絶対収束)」
\begin{array}{llllll} \displaystyle \left| f(x) \right| &≤&\mathrm{Const.} \end{array}
この形が
収束条件の1つとして考えられます。
オイラーの公式と収束
これを念頭に
\begin{array}{llllll} \displaystyle e^{iθ}&=&\cos θ+i\sin θ \end{array}
「オイラーの公式」と
その「複素共役」を考えると
\begin{array}{llllll} \displaystyle |e^{iθ}|^2&=&(\cos θ+i\sin θ)\overline{(\cos θ+i\sin θ)} \\ \\ &=&\cos^2θ+\sin^2θ \\ \\ &=&1 \end{array}
これは明らかですから
\begin{array}{llllll} \displaystyle E(|e^{itx}|) &=& 1 \end{array}
特性関数の形より
|e^{itx}| の期待値が 1 である
これが明らかな事実として導けるので
この事実から
\begin{array}{llllll} \displaystyle |f(x)|&≤&E(|e^{itx}|) \end{array}
この形を考えると
特性関数の収束が導けそうだ
そんな予想を立てることができます。
凸関数と凸不等式
「特性関数の形」と「不等式の概観」から
\begin{array}{llllll} \displaystyle \phi_X(t)&=&\displaystyle E\left(e^{itX}\right) \end{array}
\begin{array}{llllll} \displaystyle |f(x)|&≤&E(|e^{itx}|) \end{array}
凸不等式が使えそうだということが分かるので
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \end{array}
凸関数である f(x)=|x| を考えて
\begin{array}{llllll} \displaystyle f\Bigl( E(X) \Bigr)&≤&\displaystyle E\Bigl( f(X) \Bigr) \end{array}
「特性関数」に「凸不等式」を適用すると
\begin{array}{ccccll} \displaystyle \left| E\left(e^{itx}\right) \right| &≤& \displaystyle E\left(\left| e^{itx} \right|\right) \\ \\ \displaystyle \left| E\left(e^{itx}\right) \right| &≤&1 \\ \\ \displaystyle \left| \phi_X(t) \right| &≤&1 \end{array}
その結果として
このような関係が導かれます。
複素関数の収束
複素関数の絶対値が有限の範囲に収まる以上
\begin{array}{clllll} \displaystyle z&=&a+bi \\ \\ |z|&=&\sqrt{a^2+b^2} \end{array}
虚部も実部も有限の値になる
\begin{array}{llllll} \displaystyle \lim_{a \to \pm\infty} \sqrt{a^2+b^2}&=&\infty \\ \\ \displaystyle \lim_{b \to \pm\infty} \sqrt{a^2+b^2}&=&\infty \end{array}
これは明らかですから
\begin{array}{llllll} \displaystyle \sqrt{a^2+b^2}≤1 &&\to&& \begin{array}{llllll} \displaystyle -1 <a < 1 \\ \\ -1 <b <1 \end{array} \end{array}
以下の不等式が正しいということは
\begin{array}{llllll} \displaystyle \left| E\left(e^{itx}\right) \right| &≤&\displaystyle 1 \end{array}
「特性関数」が
\begin{array}{cccllllll} \displaystyle \phi_X(t)&=&E\left(e^{itx}\right) \\ \\ &=&z \end{array}
\begin{array}{clllll} \displaystyle r&≤&1 \\ \\ \sqrt{a^2+b^2}&≤&1 \end{array}
必ず実部と虚部が \infty ではない
なんらかの値 z=a+bi になる
つまり「必ず収束する」
ということを意味します。
特性関数の存在
まとめると
\begin{array}{ccccll} \displaystyle \left| E\left(e^{itx}\right) \right| &≤& \displaystyle E\left(\left| e^{itx} \right|\right) \\ \\ \displaystyle \left| E\left(e^{itx}\right) \right| &≤&1 \\ \\ \displaystyle \left| \phi_X(t) \right| &≤&1 \end{array}
\begin{array}{llllll} \displaystyle \phi_X(t)&=&\displaystyle \int e^{itx}f(x) \,dx \end{array}
「特性関数が収束する」
これが『確率密度関数に関係なく』
明らかであることから
\begin{array}{llllll} \displaystyle \int_{-\infty}^{\infty} f(x) \,dx&=&1 \end{array}
確率密度関数 f(x) がどんな分布であっても
f(x) が確率密度関数であるのなら
(積分できる・全域で積分すると結果が 1 )
\begin{array}{llllll} \displaystyle \left| \phi_X(t) \right| &≤&1 \end{array}
必ず一定の値に収束するので
特性関数は必ず存在すると言えます。
証明の補足
ぼかした部分について
大まかにまとめておきます。
\begin{array}{llllll} \displaystyle \displaystyle e^{itx}&=&\displaystyle 1+itx+\frac{(it)^2}{2!}x^2+\frac{(it)^3}{3!}x^3+\cdots \\ \\ &=&\displaystyle \cos (tx) +i\sin (tx) \end{array}
「複素数の微分(実数とほぼ同じ)」とか
「マクローリン展開」については
長くなるのでさすがに省略しますが
\begin{array}{llllll} \displaystyle f\Bigl( E(X) \Bigr)&≤&\displaystyle E\Bigl( f(X) \Bigr) \end{array}
この関係については
この記事できちんと説明しておきます。
凸関数 Convex Function
|| いろいろ嬉しい性質を持ってる関数
∪ みたいな形の関数のこと。
\begin{array}{llllll} \displaystyle a&<&b \end{array}
\begin{array}{llllll} \displaystyle p+q=1 &&0≤p,q \end{array}
\begin{array}{llllll} \displaystyle f\Bigl(qa+pb \Bigr)&≤&qf(a)+pf(b) \end{array}
\begin{array}{llllll} \displaystyle 0&≤&p&≤&1 \end{array}
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
逆の形は「凹関数」と呼ばれます。
(凸が ∪ なので形的には逆になってます)
凸関数の定義の解説
なんかちょっとややこしいですが
\begin{array}{llllll} \displaystyle 0&≤&p&≤&1 \end{array}
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
こうやって図形で考えると
\begin{array}{cccccll} \displaystyle f(x)&≤&直線 \\ \\ \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
わりと普通のことしか言ってません。
以下の式が
\begin{array}{llllll} \displaystyle a&<&b \\ \\ a&<&a+dx \end{array}
\begin{array}{llllll} \displaystyle (1-p)a+pb&=&(1-p)a+p(a+dx) \\ \\ &=& a+pdx \end{array}
↓
\begin{array}{llllll} \displaystyle a &&p=0 \\ \\ a+pdx && 0<p<1 \\ \\ b&&p=1 \end{array}
座標 a,b の間を
\begin{array}{llllll} \displaystyle (1-p)f(a)+pf(b) \end{array}
↓
\begin{array}{cccclll} \displaystyle f(a)&&p=0 \\ \\ (1-p)f(a)+pf(b) && 0<p<1 \\ \\ f(b) &&p=1 \end{array}
\begin{array}{llllll} \displaystyle (1-p)f(a)+pf(b)&=&f(a)-pf(a)+pf(b) \\ \\ &=&\Bigl( f(b)-f(a)\Bigr)p+f(a) \end{array}
これが直線を表している
この辺りがちょっと難解かもしれませんが
ここが分かれば特に疑問は出ないでしょう。
凸不等式 Jensen’s Inequality
これは名前の通り
「凸関数」の性質から導かれるもので
\begin{array}{llllll} \displaystyle 0&≤&p&≤&1 \end{array}
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
そのまま「凸関数の定義」として採用されています。
(イェンセンの不等式とも言われます)
この式から
\begin{array}{llllll} \displaystyle f\Bigl( E(X) \Bigr)&≤&\displaystyle E\Bigl( f(X) \Bigr) \end{array}
この関係が導かれるわけですが
この時点じゃなんでこうなるのか
よく分からないと思うので
これから軽く説明していきます。
凸不等式の拡張
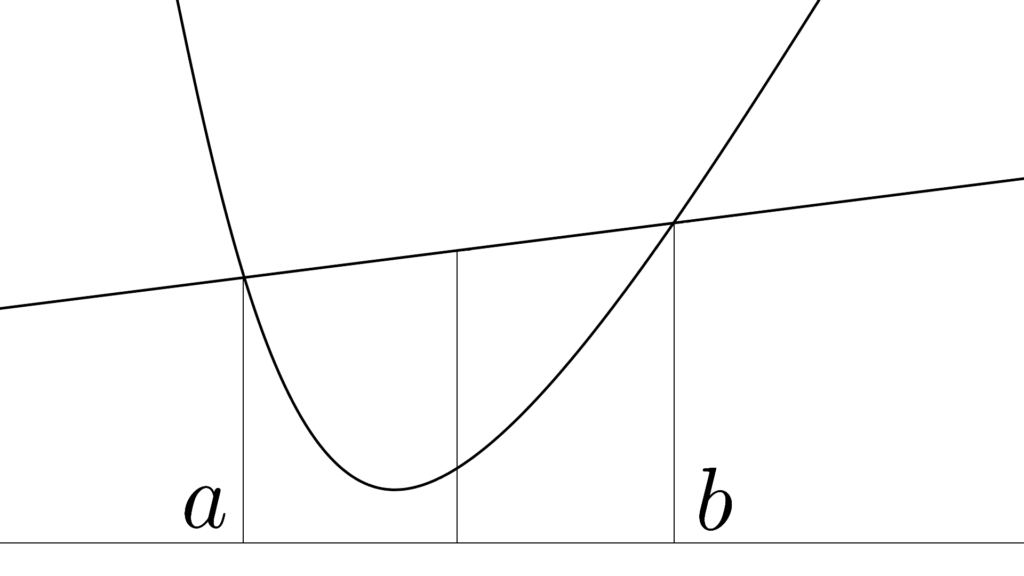
先に紹介した凸不等式は
a,b 内のどこかの点 p(b-a)+a で
直線 [a,b] を 2 分割したものです。
\begin{array}{llllll} \displaystyle 0&≤&p&≤&1 \end{array}
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
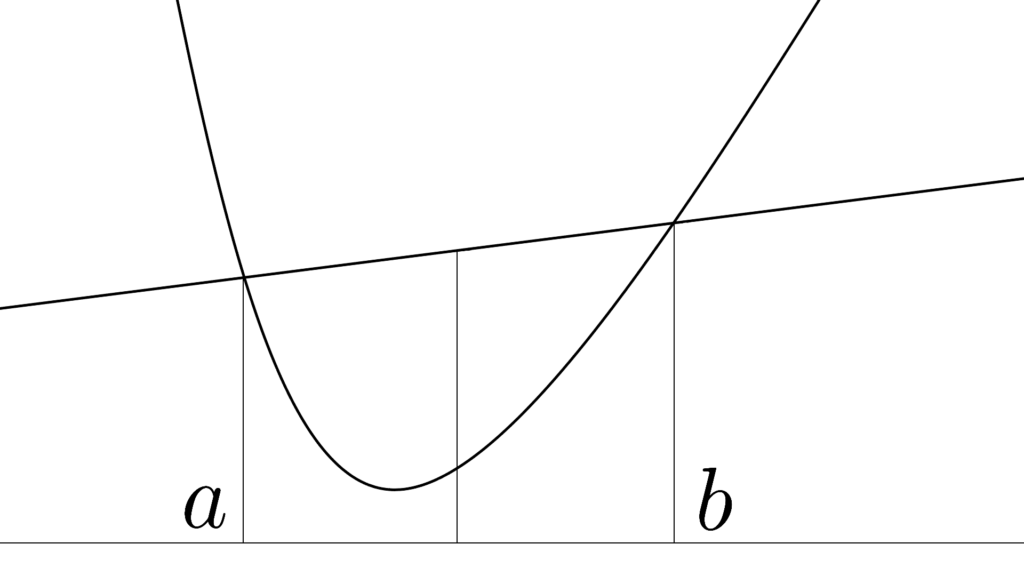
図にするとすごく単純で
f(x)<直線 の式だとすぐ分かるわけですが
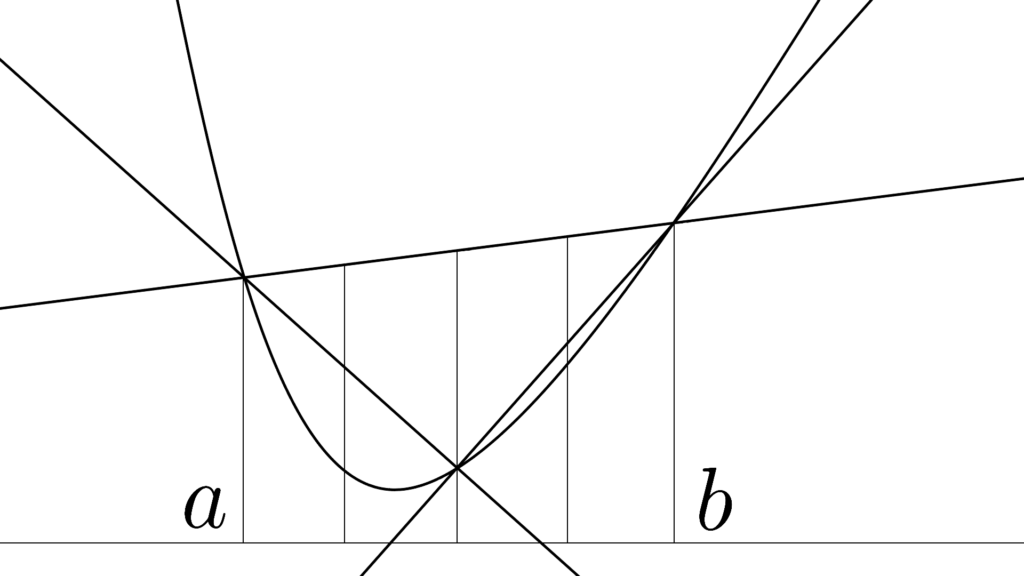
これ、同様の理屈を用いれば
何分割しても同様の結果が得られますよね。
\begin{array}{llllll} \displaystyle 0≤p_i&& 2≤n&&\displaystyle \sum_{i=1}^np_i=1 \end{array}
\begin{array}{llllll} \displaystyle f(p_1x_1+\cdots+p_nx_n) &≤&p_1f(x_1)+\cdots+p_nf(x_n) \\ \\ \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \end{array}
とするとその事実から
こんな式が得られるわけですが
これを見てわかる通り
これがほぼそのままこの記事の主題に繋がります。
本当にこうなるか確認
↑ の一般化された式が正しいかどうか。
これを確認するために
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
前提として
この定義に問題が無いとします。
( n=2 のパターンの正しさは明らか)
そこから
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \end{array}
帰納的に考えるために
凸不等式の形に寄せていくと
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right) &=&\displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n}} p_ix_i+p_{n+1}x_{n+1} \right) \\ \\ &=&\displaystyle f\left( \frac{(1-\textcolor{skyblue}{p_{n+1}})}{(1-\textcolor{skyblue}{p_{n+1}})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i+\textcolor{skyblue}{p_{n+1}}x_{n+1} \right) \end{array}
この式が得られますから
\begin{array}{llllll} \displaystyle f\Bigl((1-p)a+pb \Bigr)&≤&(1-p)f(a)+pf(b) \end{array}
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right) &=&\displaystyle f\left( \frac{(1-p_{n+1})}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i+p_{n+1}x_{n+1} \right) \\ \\ \\ \displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right)&≤&\displaystyle (1-p_{n+1})f\left( \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i \right)+p_{n+1}f(x_{n+1}) \end{array}
こうなって
\begin{array}{llllll} \displaystyle \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i &=&\displaystyle\sum_{i=1}^{\textcolor{pink}{n}}\frac{p_i}{(1-p_{n+1})} x_i \end{array}
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \\ \\ \displaystyle f\left( \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i \right)&≤&\displaystyle \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_if(x_i) \end{array}
帰納法の仮定から
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right)&≤&\displaystyle (1-p_{n+1})f\left( \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_ix_i \right)+p_{n+1}f(x_{n+1}) \\ \\ \\ \displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right)&≤&\displaystyle (1-p_{n+1})\left( \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_if(x_i) \right)+p_{n+1}f(x_{n+1}) \end{array}
こうなるので
後は式変形して帰納法の形にすれば
\begin{array}{llllll} \displaystyle (1-p_{n+1})\left( \frac{1}{(1-p_{n+1})}\sum_{i=1}^{\textcolor{pink}{n}} p_if(x_i) \right)&=&\displaystyle \sum_{i=1}^{\textcolor{pink}{n}} p_if(x_i) \end{array}
\begin{array}{llllll} \displaystyle \sum_{i=1}^{\textcolor{pink}{n}} p_if(x_i)+p_{n+1}f(x_{n+1}) &=& \displaystyle \sum_{i=1}^{\textcolor{pink}{n+1}} p_if(x_i) \end{array}
\begin{array}{llllll}\displaystyle f\left( \sum_{i=1}^{\textcolor{pink}{n+1}} p_ix_i \right)&≤&\displaystyle\sum_{i=1}^{\textcolor{pink}{n+1}} p_if(x_i) \end{array}
結果、こうなるので
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \end{array}
帰納法の原理より
この仮定の正しさが確認できます。
期待値の式とそっくり
ここまで分かれば
\begin{array}{llllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \end{array}
x_i∈X とすると
後はもう書き換えるだけで
\begin{array}{llllll} \displaystyle \sum_{i=1}^{n} p_i &=& 1 \\ \\ \displaystyle \sum_{i=1}^{n} p_ix_i &=& E(X) \\ \\ \displaystyle \sum_{i=1}^{n} p_if(x_i) &=&E\Bigl(f(X) \Bigr) \end{array}
\begin{array}{ccccllll} \displaystyle f\left( \sum_{i=1}^{n} p_ix_i \right) &≤&\displaystyle \sum_{i=1}^{n} p_if(x_i) \\ \\ \\ \displaystyle f \Bigl(E(X) \Bigr) &≤&\displaystyle E\Bigl(f(X) \Bigr) \end{array}
この式が得られます。
