|| 幾何学って何?を考える分野
だいたい「公理」の見直しをするための分野
スポンサーリンク
目次
ユークリッド原論「教養数学の原典」
公準「幾何学で採用されてる公理」
ヒルベルトの公理系「ちゃんとやる感じ」
概念の定義「線分・長さ・角度やら」
公理「点・直線・平面やらを定義する」
タルスキの公理系「他の方法で整理した感じ」
公理「図形の基礎的な性質を記述」
ユークリッド原論 Στοιχεῖα
|| 幾何学の大元になったやつ
古代数学をほぼ全てまとめたやつで
数学の地位を確立した古代ギリシア数学の集大成
教科書として長年重宝されており
聖書に次いで最も多く読まれたとされています。
「幾何学原論」とも呼ばれ
内容は「幾何学」とか「数論」とか。
もちろん「公準」もここに含まれます。
概念の定義
『点』『線』とかの概念を
このユークリッド原論はちゃんと定めています。
「点」とは部分をもたないものである
「線」とは幅のない「長さ」である
「線」には厚さが無い
「長さ」は線の第一の属性である
「長さ」は異なる線を比較しうる指標である
「線の端」は「点」である
「点」は「線の部分」である
「直線」とは
『その上にある点』が「一様に横たわる線」である
『有限な直線』を「線分」という
「面」とは
「長さ」と「幅」のみをもつものである
「幅」は面の第一の属性で「長さ」を前提とする
「面の端」は「線」である
「線」は「面の部分」である
「平面」とは
『その上にある直線』が「一様に横たわる面」である
「平面角」は「平面上に存在」して
「互いに交わり」かつ「一直線をなすことのない」
「二つの線相互の傾き」である
平面角とは平面上の「角」のこと
(そのまま角ともいう)
「角をはさむ線」が「直線」であるなら
その時の「角」は「直線角」と呼ぶ
以下、いろいろ
需要があればまた別途まとめますが
原論での概念はこんな感じです。
公準 Postulate
|| 図形がどういう感じかを決めてるやつ
図形についての5つの公理のようなもの
直線の存在
『任意の点から他の点に直線を引ける』
延長線の存在
『有限の直線を連続的にまっすぐ延長できる』
円の存在
『任意の中心と半径で円を描ける』
直角の存在
『すべての直角は互いに等しい』
平行線の存在
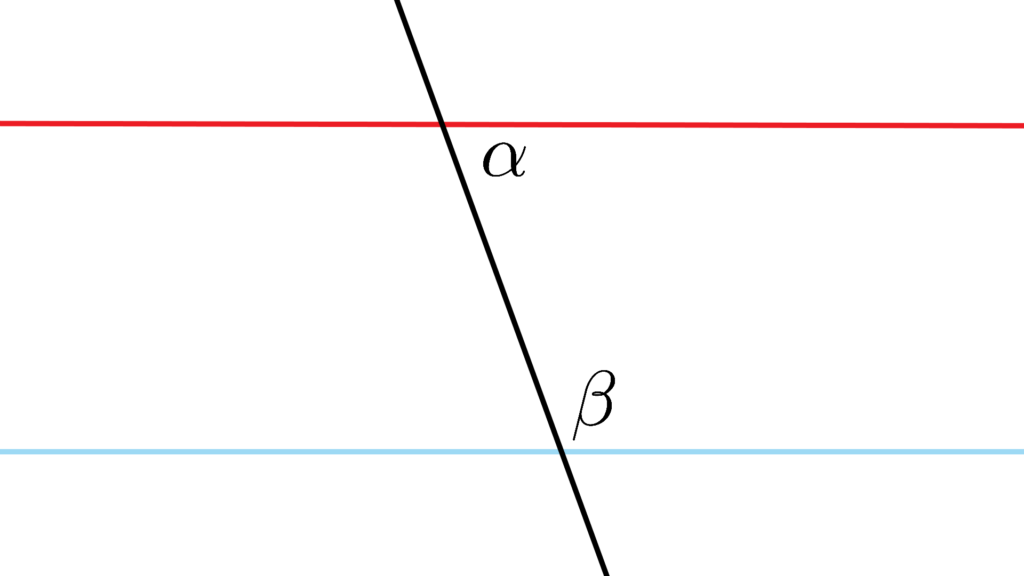
『角度 α+β が 直角 \times 2 より小さい』なら
『赤線と青線は延長するといずれ交わる』
これらはいずれも「公理」のように振舞いますが
『正しいとして良いのか分からない』ため
「公準」とも呼ばれています。
実際、5つ目の平行線公準については
採用しなくても幾何学が成立します。
(非ユークリッド幾何学)
共通の公準
幾何学に限らず成立するとされる
9つの公準もまた存在します。
『 a に等しい他のやつらは互いに等しい』(同一律)
『 a に b を加えると合計は a+b 』(可算の一意性)
『 a から b を引くと残りは a-b 』(減算の一意性)
『違うものに a を加えるとその合計は異なる』(同一律)
『 a の 2 倍は常に 2a 』(乗算の一意性)
『 a の半分は必ず a の半分』(除算の一意性)
『互いに重なり合うものは互いに等しい』(同一律)
『全体はその一部より大きい』(大小関係)
『 2 つの線分では面積を囲めない』(図形の性質)
最後のやつが幾何学の公準じゃない
これについては なんで?ってなっちゃいますけど
その他に対して
内容を直感的に理解するなら
特に疑問に思う余地は無いと思います。
ヒルベルトの公理系
|| ユークリッド原論を厳密に表現しよう
ユークリッド原論の問題点を改善したやつ
言い回しに自明な前提が多過ぎるだとか
それ必要?って感じだとか
そういうのをこれは解決しています。
定義が不十分
ユークリッド原論は
直感的にはしっかりしてますが
なんかふわっとしてる感じがどうしても拭えません。
「点」とは部分をもたないものである
「線」とは幅のない「長さ」である
「長さ」は線の第一の属性である
とまあこの辺りを切り取っても
なんか、厳密じゃない。
いずれもなんとなくは分かりますが
厳密にはどうなの?ってなると
なんだか非常に怪しく見えてきます。
実際
『点』の存在は直感的に明らかですが
原論の定義だとどうしても不十分な感じがします。
『直線』の定義にしても
「一様に横たわる」ってのを
数学的にどう表現すればいいのかよく分かりませんし。
ヒルベルトによる概念の定義
『点』『直線』『平面』など
「単体では定義が困難」なものがあって
それらは『公理』によって定義されています。
具体的には
『点』と『直線』だと
『公理』→『点はそういう感じ』
「そういう感じのやつ」→『点』
『公理』→『直線はそういう感じ』
「そういう感じの点の集まり」→『直線』
という感じに
「持ってる性質」というか
「振る舞い」から間接的に定義されます。
線分 Line Segment
異なる2点 A, B があるとして
「 A, B の間にある点の集まり」が線分 AB です。
この時の点 A,B をその「端点」と呼びます。
それと
直線 AB 上の「線分の内側にある点」が「内点」
直線上だけど「線分の外側にある点」が「外点」です。
長さ Length
「線分」を定義している『端点』の
「隔たりの大きさ」を表す「測度」のこと。
\begin{array}{llllll} \displaystyle μ \Bigl( [a,b)\Bigr) &=& b-a \end{array}
「単位線分(長さ 1 の線分)」の
『倍数の和(少数で記述できる状態)』として
\begin{array}{llllll} \displaystyle n&∈&\{0,1,2,3,4,5,...\} \end{array}
\begin{array}{llllll} \displaystyle \mathrm{length}&=&\displaystyle n_0+\frac{1}{10^1}n_1+\frac{1}{10^2}n_1 + \cdots \\ \\ \displaystyle \mathrm{length}&=&\displaystyle n_0+\frac{1}{2^1}n_1+\frac{1}{2^2}n_1 + \cdots \end{array}
『正の実数』で与えられていて
\begin{array}{l} \begin{array}{llllll} 0≤n \\ \\ \displaystyle 0≤\frac{1}{10^n} \end{array} && → && \displaystyle 0≤\mathrm{Length} \end{array}
これにより
「長さ・面積・体積」なんかの
「非負性」が保証されたりします。
距離 Distance
平面内の2点 A, B に対して
「線分 A, B の長さ」を
「点 A と点 B の距離」と言います。
側 Side
平面から直線を除いた部分のこと。
← を左側 → を右側みたいに呼ぶ感じ。
分割で使う概念で
直線の場合は点で線を分割する感じになります。
でまあ当然ですが
これは以下のような性質を持ちます。
同じ側の2点を結ぶ線分は直線と交わらない
異なる側の2点を結ぶ線分は直線と交わる
点 O で分割だったら
同じ側の2点を結ぶ線分は点 O を通らない
異なる側の2点を結ぶ線分は点 O を通る
半直線・半平面 Half
直線上の点 O を考えた時
点を挟んだ線の側に点 O を付け加える
そういった直線を区切って分割したやつを半直線
直線を隔てた平面
そこに直線を加えた側を半平面と言います。
まあ要は
「区切った直線」が半直線
「分割した平面」が半平面です。
円 Circle
ある1点 O から一定の距離にある
『平面上の点の集合』を「円」と言います。
この時の
『点 O 』が「円」の「中心」
『中心と円上の点の距離』が「半径」です。
角 Corner
\angle AOB のことですが
これの厳密な定義はちょっと込み入ってて
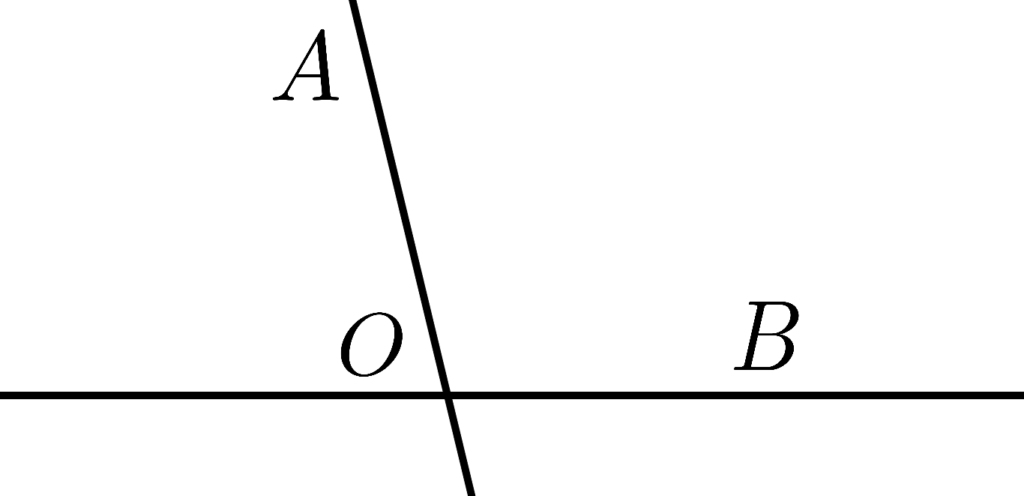
この時の O を端点とする半直線 OA,OB
この「組 (OA,OB) 」を『角』と言い
これらがなす半平面 P_A,P_B の
共通部分 P_A∩P_B を「角」の『内部』と言います。
言い回しがあれですが
まあ要は「2つの線の交点周り」が『角』で
「4分割された内の1つ」が「角の内部」です。
で、この時の「点 O 」が「頂点」
線分 OA,OB が「辺」になります。
ちなみに記号 \angle AOB は
「角」も「角度」も表す記号なので
ちょっとややこしいです。
角度 Angle
「角の大きさ」を表現する「測度」のこと。
\begin{array}{llllll} \displaystyle 180\degree&=&π \, \mathrm{radian} \end{array}
だいたい弧度法 \mathrm{radian} で書かれます。
直角 Right Angle
直線上の点を端点とする半直線によって作られる
隣り合う2つの角が合同であるとき
それらの角を「直角」と言います。
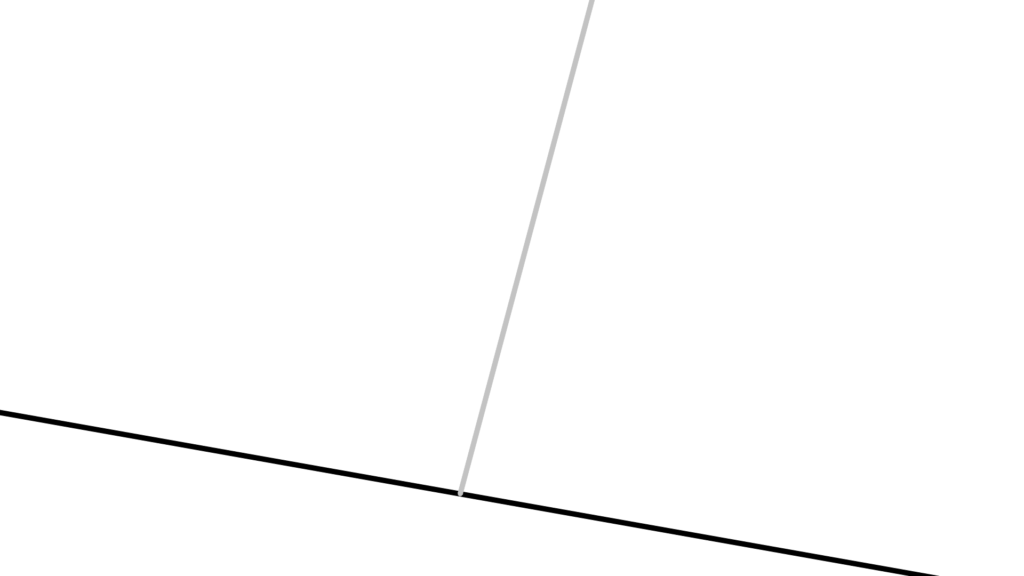
言葉で表現するとあれですが
要はこの図形が直交してる時の角が直角です。
交点 Intersection
2点を通る直線の唯一性から
2直線が共有する点があったとしても
1点のみだと分かる。
この事実から
「共有する点が存在する」時
その2直線は「交わる」と言えて
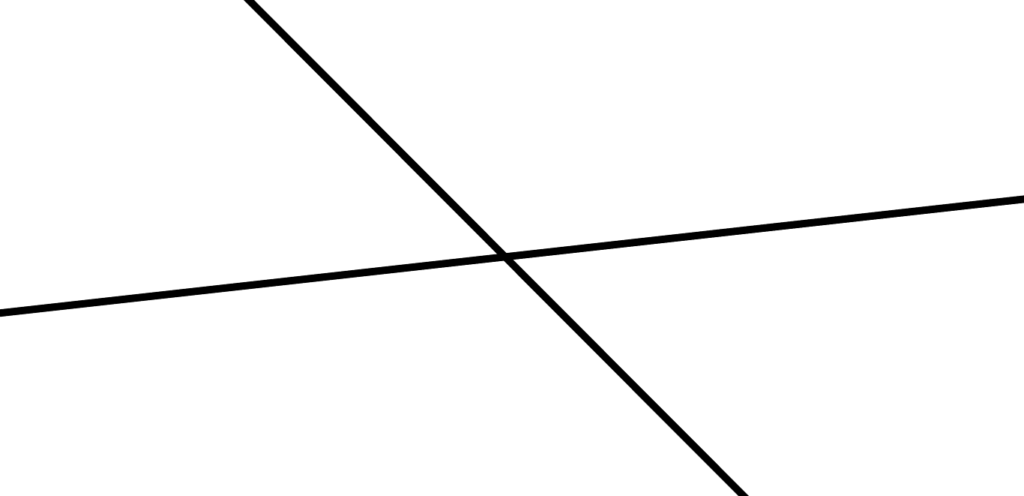
その時の『共有する点』のことを
そのまま「交点」と言います。
平行 Parallel
2直線が同じ平面にある時でも
「交点」が無い場合
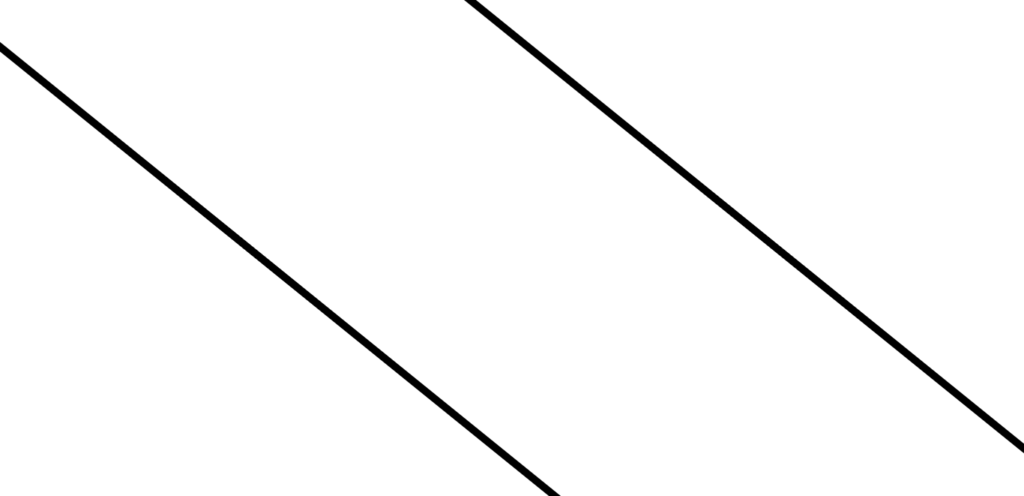
その2直線の関係を「平行」と言います。
合同 Congruence
移動させたり回転させると重なる
そんな2つの図形の「関係」を合同と言います。
\begin{array}{cccllllll} \displaystyle A&\equiv&B &&\mathrm{Point} \\ \\ AB&\equiv&CD && \mathrm{Line} \end{array}
例えば
2つの三角形が合同であるなら
\begin{array}{llllll} \displaystyle \begin{pmatrix} & A≠B \\ ∧& B≠C \\ \\ ∧&AB\equiv A^{\prime}B^{\prime} \\ ∧&AC\equiv A^{\prime}C^{\prime} \\ ∧&BC\equiv B^{\prime}C^{\prime} \end{pmatrix} &\to&\triangle{ABC}\equiv \triangle{A^{\prime}B^{\prime}C^{\prime}} \end{array}
\begin{array}{llllll} \displaystyle \begin{pmatrix} & A≠B \\ ∧& B≠C \\ \\ ∧&AB\equiv A^{\prime}B^{\prime} \\ ∧&AC\equiv A^{\prime}C^{\prime} \\ ∧&BC\equiv B^{\prime}C^{\prime} \\ \\ ∧&\angle A \equiv \angle A^{\prime} \\ ∧&\angle B \equiv \angle B^{\prime} \\ ∧&\angle C \equiv \angle C^{\prime} \end{pmatrix} &←&\triangle{ABC}\equiv \triangle{A^{\prime}B^{\prime}C^{\prime}} \end{array}
対応する辺と角度が全て合同になります。
まあ要は「図形上のイコール」です。
これにより
『同じ』っていう感覚を
図形の話に導入することができます。
結合公理
『点』『直線』『平面』については
「公理」によって間接的に定義されます。
直線を定義する公理
『2点を通る直線は少なくとも1つ存在する』
『異なる2点を通る直線は1つだけ存在する』

1つ目いる?ってなるかもしれませんが
『点が重なってるパターン』を考える時
確実に必要になります。
平面を定義する公理
『同じ直線上にない3点を含む平面は存在する』
『同じ直線上にない異なる3点を含む平面』は
『ただ1つだけ存在する』
これの1つ目も
「直線」と同様の理由で必要になります。
次元を定義する公理
『一直線上にある異なる点は少なくとも2つ存在する』
『一直線上にない3つの異なる点が存在する』

『同一平面上にない異なる4つの点が存在する』
とまあこんな具合で
この辺はまあそうでしょって感じです。
ただ最後
『3次元上まで』に留める役割を持つ
「平面」版の「交点」みたいな話もあって
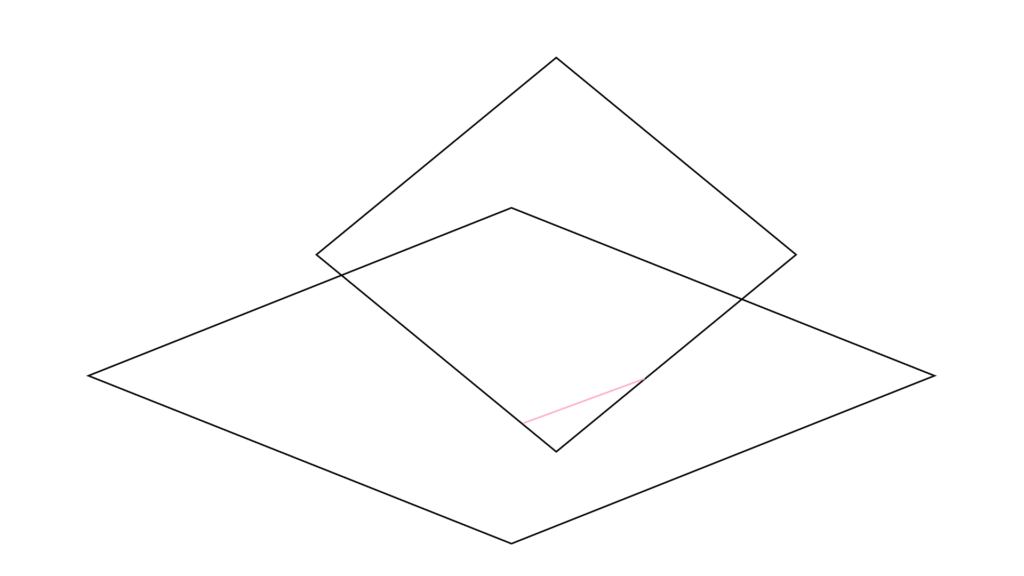
点 A が「2つの平面上に存在する」なら
「点 A とは異なる2つの平面上にある点」が
少なくとも1つは存在する
これはちょっと込み入ってます。
主張はまあ当然なんですけど。
ちなみに平面と立体で出てきた図形は
それぞれ一部を切り取ったものです。
平面に端っこはありません。
3次元まで考える
最後のは少し特殊で
例えば「4次元上」の話であれば
これは正確ではなかったりします。
というのも4次元では次元を折り畳めるので
「平面」を「直線」とみなせる角度があり
この場合、1点でのみ交わる状況を作れます。
となると「4次元まで考える」なら
この公理は正しくないことになるので
この公理を採用するということは
この「次元の折り畳みを認めない」ということ。
つまり3次元まで考える
ということになります。
直線の間接的な定義
直線の定義については
『異なる2点を通る直線は1つだけ存在する』
この公理でだいたい完結しています。
というのも
「2点を通る線」は『複数』存在するわけですが
『直線』と限定された場合では
「そういう線」は必ず一意に定まります。
まあ要は
「異なる2点が与えられた」時に
「ただ1つに定まるような線」
これが「直線」の持つ『性質の一つ』で
「直線の持つ性質」はこんな要領で増えていきます。
順序公理
これは『間に存在する』
という概念を定めるための公理と言えます。
内と外
直線上の「内」と「外」を定める公理
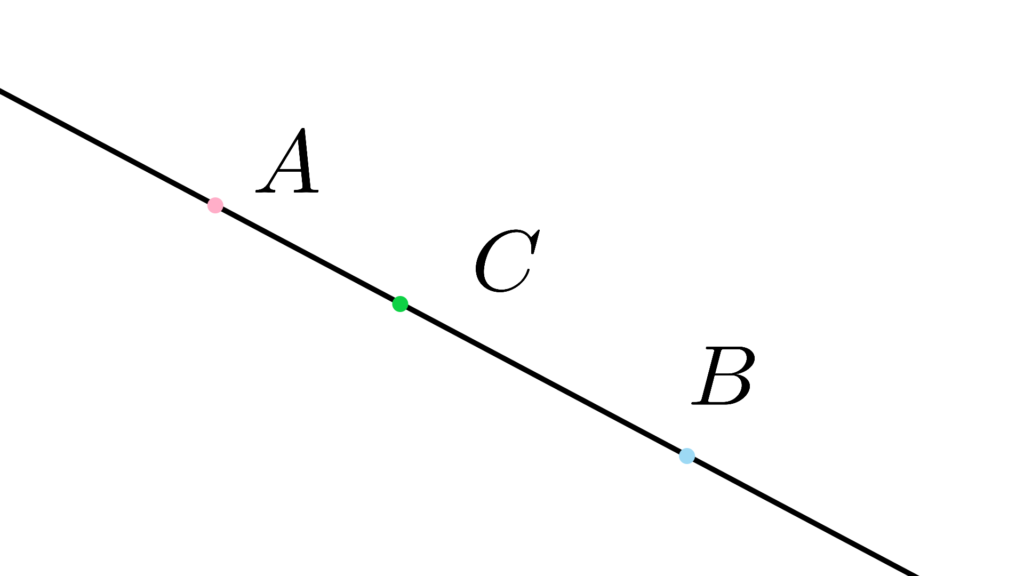
直線 l 上の点 C が
直線 l 上の『点 A,B の間に存在する』なら
点 A, B, C は一直線上の異なる点である
任意の点 A,C が存在する時
点 A と点 B の間に点 C があるような
点 C を点 A と挟む『点 B が存在する』
これは挟む方の公理が
「重なる」パターンをカバーしていて
1つ目がざっくりと『間にある』を定義しています。
結合の由来
↑ 2つの公理を認めると
\begin{array}{llllll} \displaystyle AC+CB&=&AB \end{array}
こんな感じの
『直線の足し算』のような操作が考えられます。
これが「結合」の感覚で
この場合「間」は「連結した点」を表しています。
順番
「一直線上にある任意の3点」を考える時
「その内の2点を選ぶ」と
\begin{array}{llllll} \displaystyle A&C&B \\ \\ A&C& &&→&&0 \\ \\ &C&B &&→&&0 \\ \\ A&&B &&→&&1 \end{array}
その「3つの点だけを考える」なら
『間に存在する点』は多くても1点だけである
これは他から導けそうですが
「点の位置・数」を明確に制限しているので
決して無意味なものではありません。
これを採用しない場合
「点の位置」が明確化されないので
例えば「2点の間」を考える時
そこにある点を厳密に定義できなかったりします。
(この公理が点の並び順に強く言及している)
上で話した2つの公理では
前者はそもそも並び順に言及していないですし
後者は並びに言及していますが
点が重なる場合に順番が崩れてしまうため
順番が保存されないことがあり得ます。
パシェの公理
「平面上」の「内」と「外」を定める公理
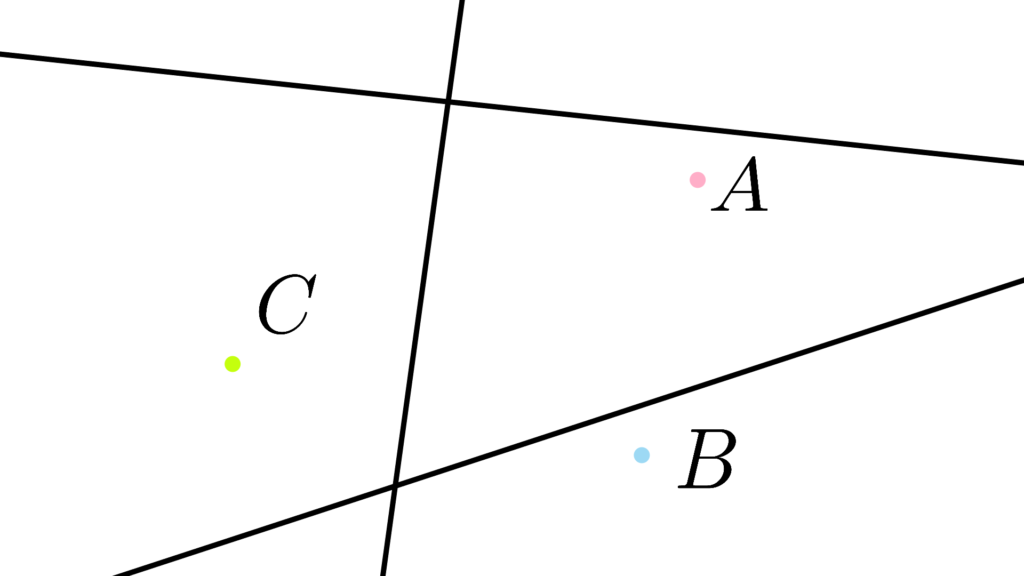
「平面の存在を定める条件」を満たす
『一直線上にない異なる3点』があるとする。
その上で
「3点を通らない平面上の直線」を考える。
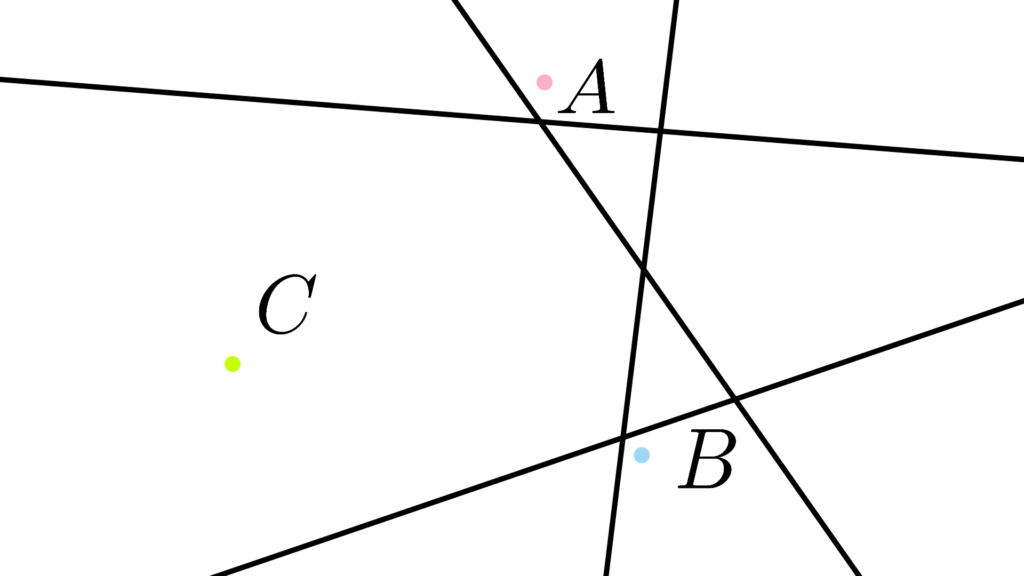
この時
直線が「線分 AB の内点を通る」なら
直線は「線分 AC か線分 BC の内点を通る」
まあつまり
3点で定まる図形があったとして
その「図形の中」を通る条件を
この公理は保証しています。
合同公理
「図形が同じ」を定義するための公理
「図形が同じ」であることを表現する時
「記号 \equiv 」がよく使われます。
直線の同値性
ある「直線」が『同じ』という感覚を表す
最低限の性質が宣言されています。
直線 l 上にある異なる点 A, B がある。
直線 l^{\prime} 上にある点を A^{\prime} とする。
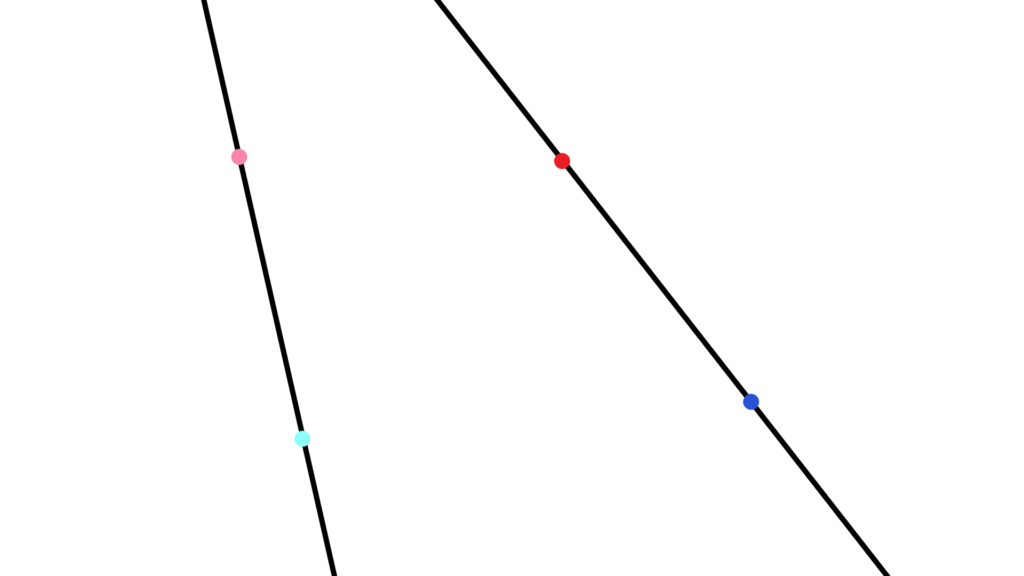
直線 l^{\prime} 上に
AB ≡ A'B' を満たすような点 B^{\prime} が存在する。
まあ要は「同じ線分が作れる」感じで
これのおかげで『同じ線』を任意に作れるように。
またこれに関わる公理として
\begin{array}{llllll} \begin{pmatrix} \displaystyle & AB≡A_1B_1 \\ ∧& AB≡A_2B_2 \end{pmatrix} &&\to&& A_1B_1≡A_2B_2 \end{array}
このような「同値性」の「推移律」も考えられ
同様に ↓ のような
「推移律」もまた考えられます。
直線 l 上に点 A,B,C がある。
点 C が点 A,B の間にある。
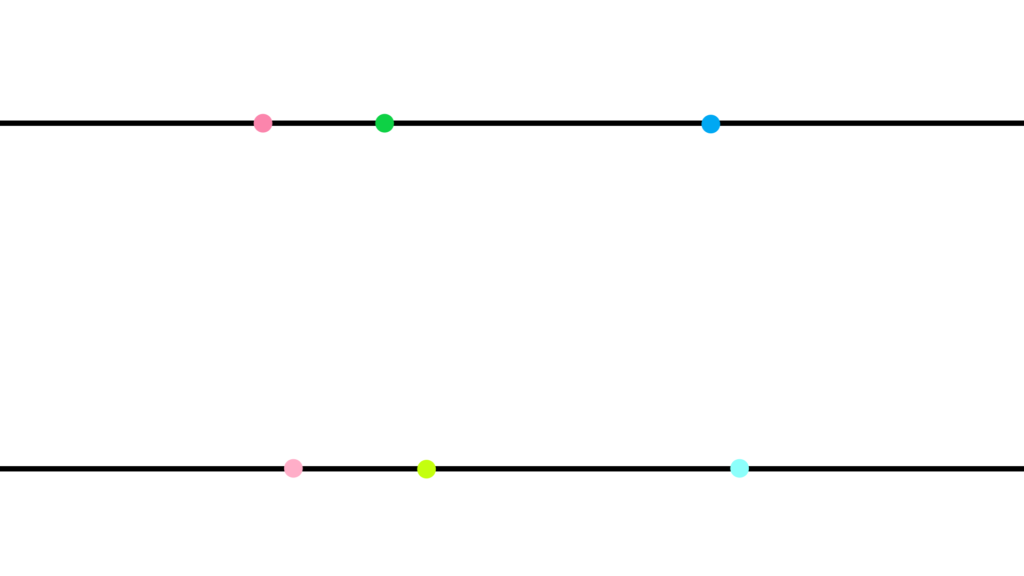
直線 l^{\prime} 上に点 A^{\prime},B^{\prime},C^{\prime} がある。
点 C^{\prime} が 点 A^{\prime},B^{\prime} の間にある。
\begin{array}{llllll} \displaystyle \begin{pmatrix} &AC ≡ A^{\prime}C^{\prime} \\ ∧& CB ≡ C^{\prime}B^{\prime} \end{pmatrix} &&→&& AB ≡ A^{\prime}B^{\prime} \end{array}
この時、このようになる。
これらに関しては
まあ直感的に分かると思います。
否定の余地は無いでしょう。
ちなみにこれらを応用すると
「点 A 」を中心に置いて
「線分 AB^{\prime} 」の「端点 B^{\prime} 」を全て求めれば
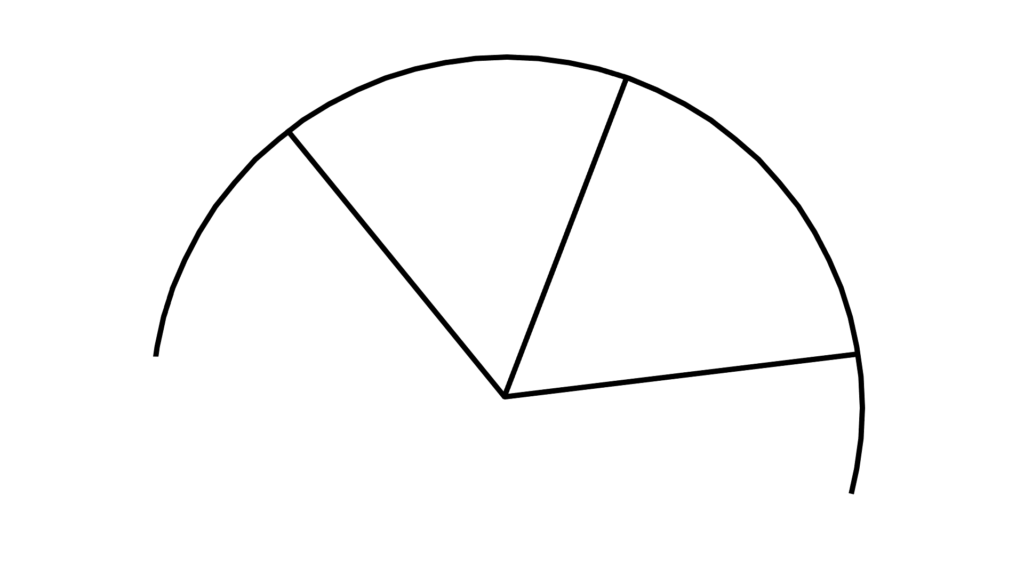
そのまま「円」が得られます。
角の同値性
「角」って概念にも
『同じ』という感覚を導入します。
\begin{array}{llllll} \displaystyle \angle (OA,OB)&\equiv&\angle (OA,OB) \\ \\ \displaystyle \angle AOB&\equiv&\angle BOA \end{array}
そのために
『任意の角はそれ自身に合同である』とし
「角が合同である」の存在を保証します。
以下、角が絡む図形の性質について
合同条件についての宣言を行います。
点 A, B, C は同一直線上に無い。
点 A^{\prime}, B^{\prime}, C^{\prime} も同一直線上に無い。
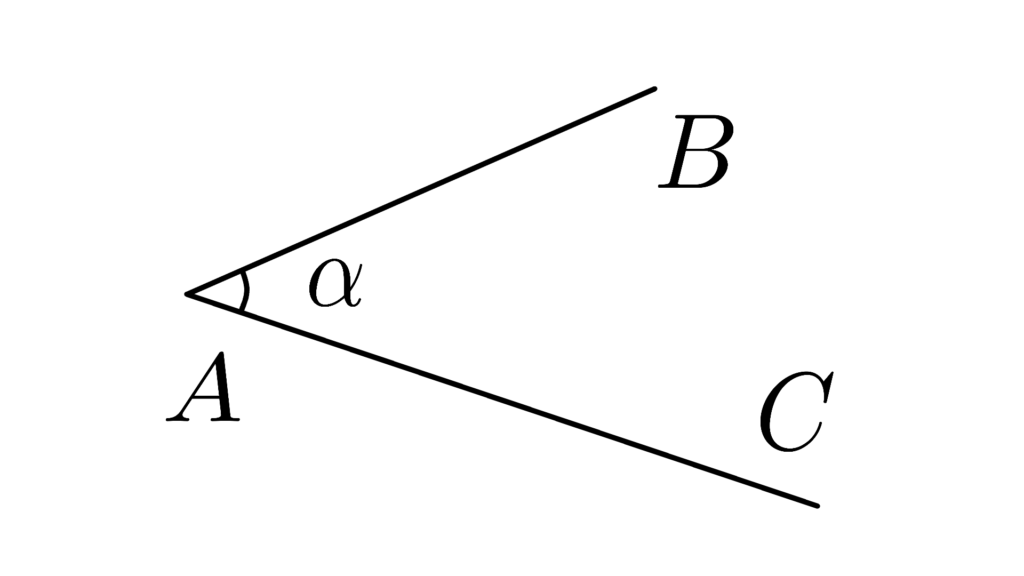
\begin{array}{llllll} \displaystyle \begin{pmatrix} & AB\equiv A^{\prime}B^{\prime} \\ ∧&AC\equiv A^{\prime}C^{\prime} \\ \\ ∧&\angle BAC \equiv \angle B^{\prime}A^{\prime}C^{\prime} \end{pmatrix} &&\to&&\angle ABC \equiv \angle A^{\prime}B^{\prime}C^{\prime} \end{array}
その時、こうなる。
いわゆる「2辺とその間の角」ってやつです。
必然的に BC \equiv B^{\prime}C^{\prime} なんかも導かれます。
この他に
より原始的なやつもあって
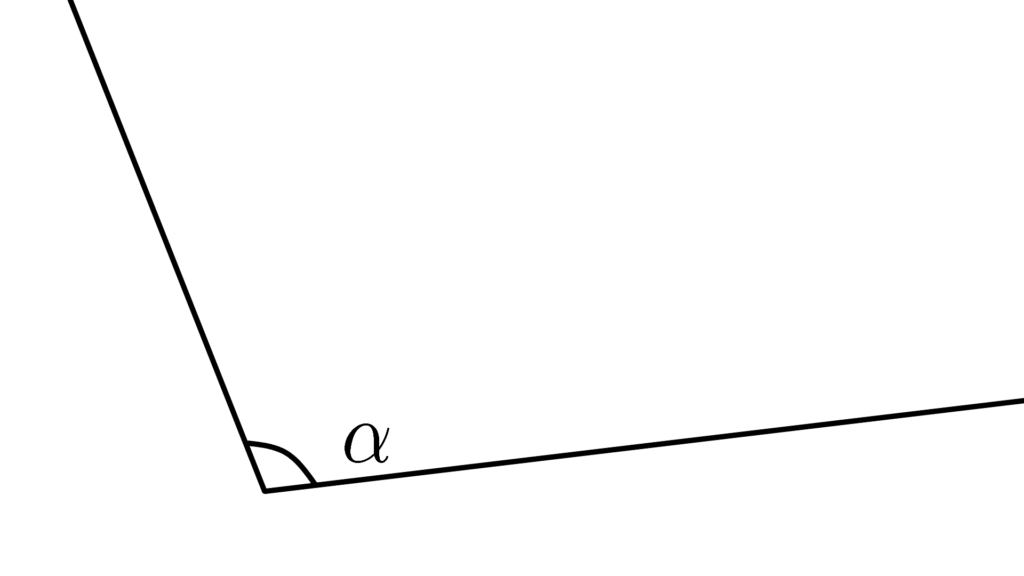
視覚的・直感的には
この「半直線の片方」と「角」が決まると
「もう片方の半直線」が『ただ一通り定まる』
とまあそんな感じなんですが
これを厳密に言語化するとややこしくなります。
以下、言語化すると
2つの半直線 m,n が同一平面上に存在する(角を定義)
2つの半直線の角 \angle (m,n) が存在する(比較対象)
直線 l が平面 P 上にあるとする
点 O を直線 l 上の一点とする
(半直線のための定義)
点 O を端点とする
直線 l に属する半直線の1つを l_h とおく
(片方の半直線の方向を1方向に定める)
直線 l を境界とする半平面を P_h とする
(注目する平面の片側を定める)
以上
「半直線 l_h 」が定まってる状態では
(平面の片側とか基準となる角とかも定まってる)
半平面 P_h 上にあるもので
点 O を端点とする
直線 l の半直線ではない半直線 k_h の中で
\begin{array}{llllll} \displaystyle \angle (m,n) &\equiv & \angle (l_h,k_h) \end{array}
この条件を満たすものがただ1つだけ定まる。
(角+片方の半直線 → もう片方の半直線)
平行線公理
これはまあそのまま。
「平行線の存在」についての宣言で
現在は「プレイフェアの公理」
なんて呼ばれるものが採用されています。
中身は「平行線公準」より簡単
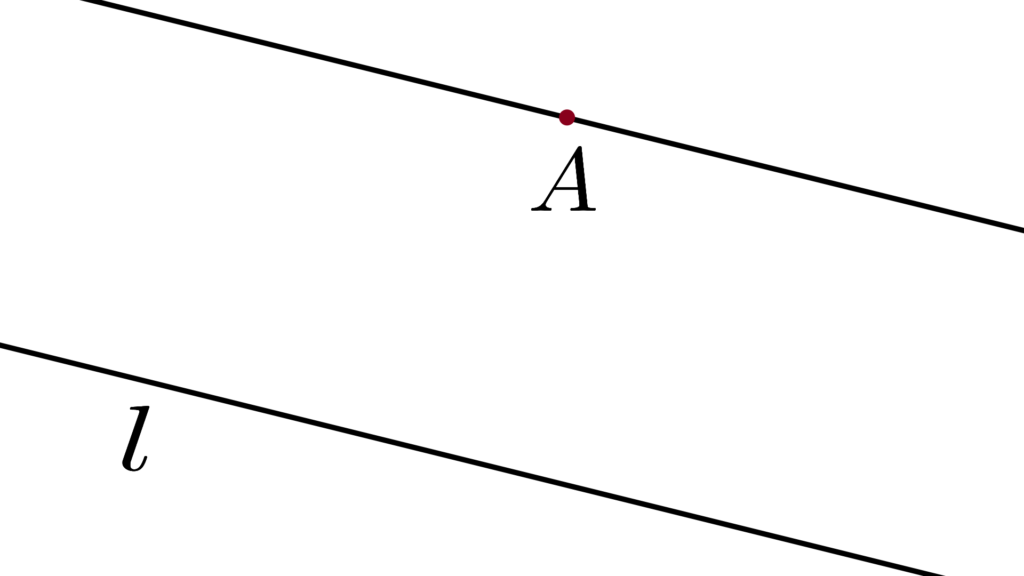
任意の直線 l と点 A がある時
A を通り l に平行な直線が 1 本だけ存在する
これが「プレイフェアの公理」で
この採用によって「平行線の存在」は保証されます。
連続性公理
ユークリッド平面と実数平面 R^2 が同値である
とかなんとか、そんな感じの話なんですが
ちょっと簡単に説明するのが難しいです。
アルキメデス性(無限が出ない)については
特に疑問の余地は無いんですけど
公理の拡張性がうんたらの話は
ちょっと直感的じゃないと思います。
アルキメデス性
実数直線との関わりを持たせるための公理です。
線分を有限個に分割して連続性を保証します。
\begin{array}{llllll} \displaystyle AB&&→&& A_0A_1,& A_1A_2,& A_2A_3,& \cdots & A_{n-1}A_n \end{array}
線分 AB は
その中の有限個の点 A_0,A_1,A_2,...,A_n で
このように分けることができる。
それを踏まえた上で
任意の線分 PQ があったとして
この線分 PQ と合同な線分 AA_1 が作れる。
とまあこんな感じなんですが
これはまあ当然っちゃ当然。
どの線分にも特に制限は無いので
PQ が定まった後に AB を定めれば
そりゃ作れます。
でまあこの操作が可能なので
ほぼ点の短い線分 PQ を考えても
それを「線分 AB の中に収めることができる」ので
結果、連続性が保証される。
とまあこんな感じに
連続性の定義と似た形でこれは宣言できます。
整合性の保証
「完備性」についての話で
「順序公理」「合同公理」「アルキメデス公理」
この辺りの話が絡んでるんですが
これは必要になった経緯とか
そういうとこから入らないといけないので省略。
「完備距離空間」の記事とかでやります。
タルスキの公理系
|| ヒルベルトさんとは異なるやり方
ヒルベルトの公理系より使いやすくした感じ。
20 以上の図形的な性質を記述した感じで
\begin{array}{llllll} \displaystyle AB&\equiv&BA \end{array}
だいたい「同じ長さ」「合じ形」を意味する
「合同 \equiv 」の記号で書かれてます。
他にも『直線上の点』を定義するために
「点 B 」が「点 A と点 C 」の
「間にある \mathrm{betweenness} 」を意味する
\begin{array}{llllll} \displaystyle \mathrm{Bet}(ABC) \end{array}
こういった記号も多く使われてますね。
点の同一性
記号の意味が分かれば説明不要だと思います。
\begin{array}{llllll} \displaystyle \mathrm{Bet}(ABA)&\to&A=B \end{array}
「点 A と点 A の間」には
当然「点 A しかない」ので
特に疑問は無いでしょう。
線の同一性
A,B は点を表すとし
AB は点 A,B を通る線分を表すとします。
\begin{array}{cccccccccl} \displaystyle AB\equiv BA \\ \\ AB \equiv PQ &∧&AB\equiv ST &\to&PQ\equiv ST \\ \\ AB\equiv CC &\to&A=B \end{array}
すると「線分の同一性」に関してはこんな感じに。
公理というだけあって当たり前すぎるので
特に疑問に思うところは無いと思います。
線の可算
ある線にある線を付け足せる
\begin{array}{llllll} \displaystyle ∃X &\Bigl( & \mathrm{Bet}(ABX) ∧ (BX\equiv CD) & \Bigr) \end{array}
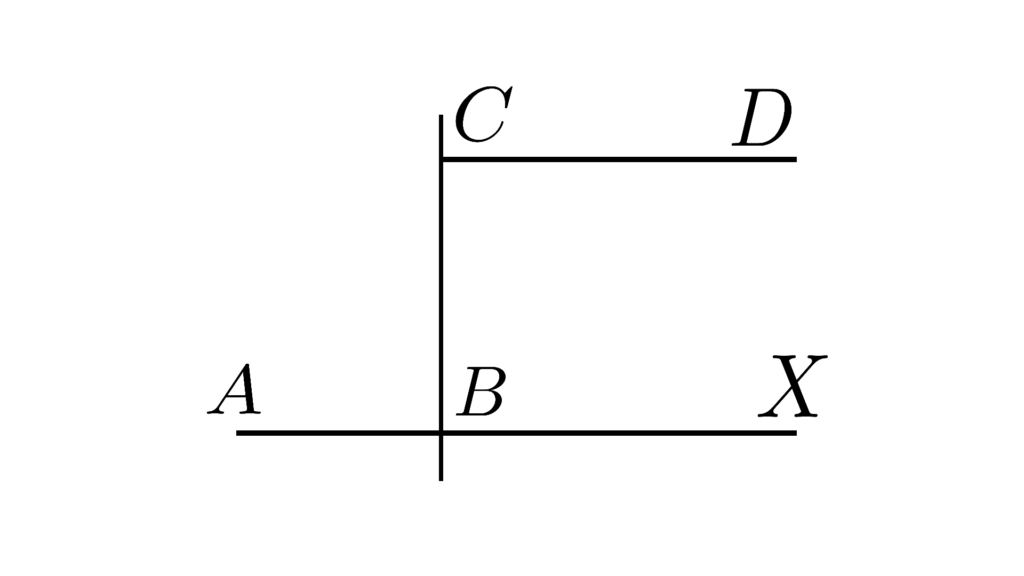
この公理はそれを保証します。
決定される線
「2つの線 CB,BD 」が交わってる時
「その角度 \angle CBD 」が決まってるなら
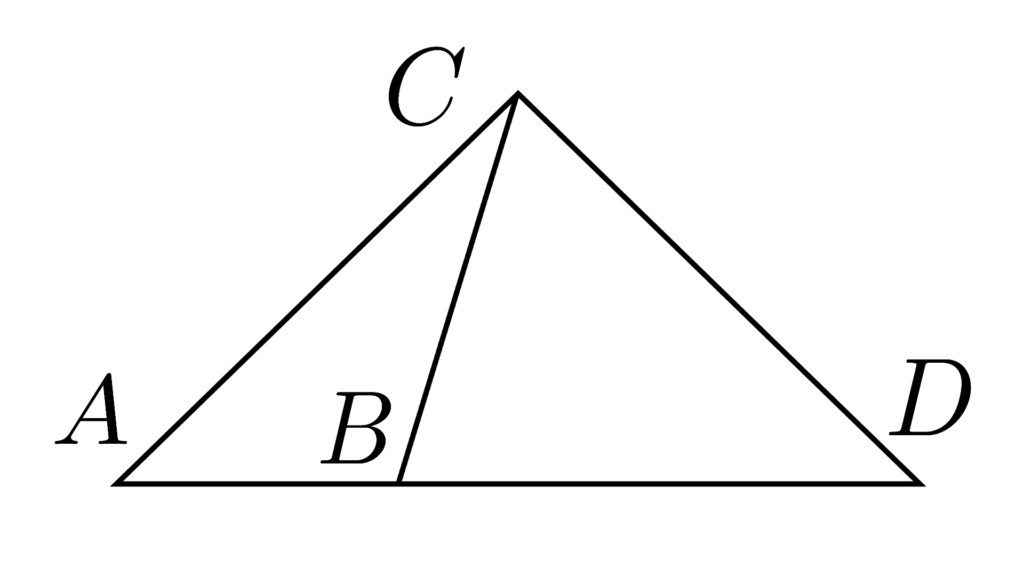
\begin{array}{llllll} \displaystyle \begin{pmatrix} & A≠B \\ ∧& B≠C \\ \\ ∧&\mathrm{Bet}(ABD) \\ ∧&\mathrm{Bet}(A^{\prime}B^{\prime}D^{\prime}) \\ \\ ∧&AB\equiv A^{\prime}B^{\prime} \\ ∧&AC\equiv A^{\prime}C^{\prime} \\ ∧&BC\equiv B^{\prime}C^{\prime} \\ ∧&BD \equiv B^{\prime}D^{\prime} \end{pmatrix} &\to&CD\equiv C^{\prime}D^{\prime} \end{array}
線 CD は一意に定まるっていう
図形の同値条件を意味する公理
複雑なようで言ってることは単純です。
以下、もっとあるんですけど
これ以上は長くなりすぎるので別記事で扱います。
