|| 積分の中でも特に複雑なやつの1つ
指数に2次の変数が来る場合の積分
スポンサーリンク
\begin{array}{llllll} \displaystyle \int_{-\infty}^{\infty} e^{-x^2} \,dx &=&\displaystyle \sqrt{π} \\ \\ \displaystyle \int_{-\infty}^{\infty} e^{-ax^2} \,dx &=&\displaystyle \sqrt{\frac{π}{a}} \end{array}
基本形はこの形になります。
ちなみにこの関数の図形は山みたいな形です。
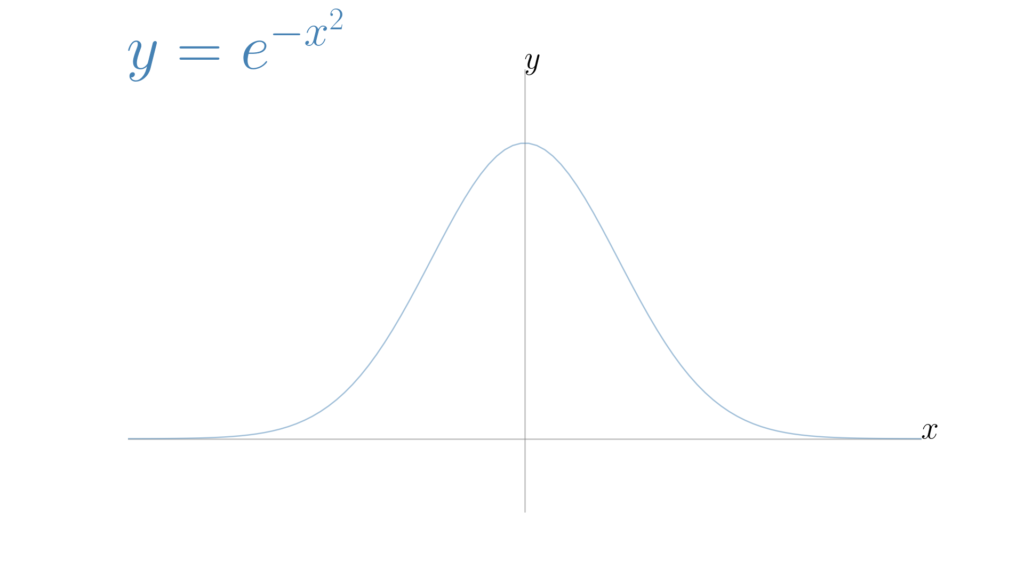
積分値を求める鍵は以下の2式
\begin{array}{llllll} \displaystyle e^{-x^2}&=&\displaystyle\int -2xe^{-x^2} \,dx \\ \\ dxdy&=&rdθdr \end{array}
ここから積分値を求める方法が得られます。
ガウス積分の導出
積分値を求める上での最大の障害は
\begin{array}{llllll} \displaystyle e^{-x^2}&=&\displaystyle \frac{d}{dx}F(x) \end{array}
「原始関数 F(x) が分からない」ことで、
このせいで積分値の計算が行えません。
\begin{array}{rcclllll} \displaystyle \frac{d}{dx}e^{-x^2}&=&-2xe^{-x^2} \\ \\ e^{-x^2}&=&\displaystyle\int -2xe^{-x^2} \,dx \end{array}
こいつ自体は簡単に微分できるんですが
\begin{array}{llllll} \displaystyle \displaystyle \int_{-\infty}^{\infty} e^{-x^2} \,dx \end{array}
これはこのままではどうしようもないです。
分かる形にしたい
以下のことは簡単に分かります。
\begin{array}{rcclllll} \displaystyle \frac{d}{dx}e^{-x^2}&=&-2xe^{-x^2} \\ \\ e^{-x^2}&=&\displaystyle\int -2xe^{-x^2} \,dx \end{array}
ということは
どうにかこの形にすれば積分できそう
\begin{array}{llllll} \displaystyle e^{-x^2}&=&\displaystyle\int -2xe^{-x^2} \,dx \end{array}
単純な発想ですが
ここに行き着く方法さえあれば
積分値を求めることはできそうです。
まあでも
そんな都合の良い方法あるんか?って話ですよね。
いやまあお察しの通り、あるんですが
これがだいぶ複雑というか面倒というか。
まあそんな感じなので、これから解説。
極座標表示
座標の表示方法は主に2通りあって
その中でも三角関数を使う方法を
「極座標」表示と言います。
\begin{array}{llllll} \displaystyle (x,y) \\ \\ (r,θ) \end{array}
\begin{array}{llllll} \displaystyle x&=&r\cos θ \\ \\ y&=&r\sin θ \\ \\ r&=&\displaystyle \sqrt{x^2+y^2} \end{array}
その中でも
特に積分は以下のような変形が可能
\begin{array}{llllll} \displaystyle \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\,dxdy \\ \\ \displaystyle \int_{0}^{2π}\int_{0}^{\infty}f(r,θ)\,rdθdr \end{array}
底面積 dxdy のとり方に違いがあって
\begin{array}{llllll} dz&=&d(x,y) \\ \\ \displaystyle dxdy &=&d(x,y) \\ \\ &=&\displaystyle \frac{d(x,y)}{d(r,θ)} d(r,θ) \end{array}
以下は
\begin{array}{llllll} \displaystyle \frac{d(x,y)}{d(r,θ)} &=&\displaystyle \frac{\partial x}{\partial θ}\frac{\partial y}{\partial r} - \frac{\partial x}{\partial r} \frac{\partial y}{\partial θ}\end{array}
「ヤコビアン」とかいう考え方から
(ざっくり言うと微小面積を求める式)
\begin{array}{lcrccclcr} \displaystyle\frac{\partial x}{\partial θ} &=&r\cos θ &&&& \displaystyle\frac{\partial y}{\partial r} &=&\cos θ \\ \\ \displaystyle \frac{\partial x}{\partial r}&=&\sin θ &&&& \displaystyle \frac{\partial y}{\partial θ} &=&-r\sin θ \end{array}
\begin{array}{llllll} \displaystyle dxdy &=& rdθdr \end{array}
このようになると言えて
この変換に伴い
全区間の定義 (a,b) も変化
(この辺りの詳細は別の記事で)
\begin{array}{rlcllll} \displaystyle -\infty&<&x&<&\infty \\ \\ -\infty&<&y&<&\infty \\ \\ \\ 0&≤&r&<&\infty \\ \\ 0&<&θ&<&2π \end{array}
結果として
「全区間 -\infty<x<\infty 」から
『無限』を取り除くことができたり
\begin{array}{llllll} \displaystyle f(x,y) &&→&&rf(r,θ) \end{array}
式の中にある変数を増やせたりだとか
そういうことができたりします。
x^2 と極座標表示
整理しておくと
\begin{array}{llllll} \displaystyle e^{-x^2}&=&\displaystyle\int -2xe^{-x^2} \,dx \end{array}
目指したい形はこれです。
\begin{array}{llllll} \displaystyle e^{-r^2}&=&\displaystyle\int -2re^{-r^2} \,dx \end{array}
この形なら計算ができるので
\begin{array}{llllll} \displaystyle x^2+y^2&=&r^2\cos^2θ+r^2\sin^2θ \\ \\ &=&r^2(\cos^2θ+\sin^2θ) \end{array}
\begin{array}{llllll} \displaystyle I&=&\displaystyle\int_{-\infty}^{\infty} e^{-x^2} \,dx \\ \\ \displaystyle I&=&\displaystyle\int_{-\infty}^{\infty} e^{-y^2} \,dy \end{array}
そのためにこうしてみる。
\begin{array}{llllll} (a_1+a_2)(b_1+b_2)&=&\displaystyle a_1b_1+a_1b_2+a_2b_1+a_2b_2 \end{array}
\begin{array}{llllll} \displaystyle \sum_{i=0}^{n}a_i\sum_{j=0}^{m}b_j &=& \displaystyle \sum_{i=0}^{n}\sum_{j=0}^{m}a_ib_j \end{array}
\begin{array}{llllll} \displaystyle I^2&=&\displaystyle\int_{-\infty}^{\infty} e^{-x^2} \,dx\int_{-\infty}^{\infty} e^{-y^2} \,dy \\ \\ &=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-x^2}e^{-y^2} \,dxdy \\ \\ &=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^2+y^2)} \,dxdy \end{array}
するとこうなるので
\begin{array}{llllll} \displaystyle I^2&=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^2+y^2)} \,dxdy \\ \\ &=&\displaystyle \int_{0}^{2π}\int_{0}^{\infty}e^{-r^2}\,rdrdθ \end{array}
計算できる形に変形できます。
重積分の感覚
積分が面積を求める計算であるように
重積分は体積を求めます。
\begin{array}{llllll} \displaystyle \int_D f(z) \,dz &=&\displaystyle\int\int_D f(x,y) \,d(x,y) \\ \\ &=&\displaystyle\int\int_D f(x,y) \,dxdy \end{array}
\begin{array}{llllll} D&=&\displaystyle [a_1,b_1]×[a_2,b_2] \\ \\ V&=& \displaystyle \int\int_{D} f(x,y) \,dxdy \\ \\ &=& \displaystyle \int \int_{[a_1,b_1]×[a_2,b_2]} f(x,y) \,dxdy \end{array}
感覚的には dxdy が底面積
f(x,y) が高さという感じでしょうか。
多重積分の怪しい部分
多重積分の計算について
詳しい話は省くんですが
\begin{array}{llllll} \displaystyle 0&<&e^{-x^2}&≤&1 \end{array}
この関数はこの範囲(正かつ有界)な上に
「全ての範囲 -\infty<x<\infty 」で連続なので
\begin{array}{llllll} \displaystyle \int_{a_2}^{b_2} \int_{a_1}^{b_1} f(x,y) \,dxdy&=&\displaystyle \int_{a_2}^{b_2} \left(\int_{a_1}^{b_1} f(x,y) \,dx \right) \, dy \\ \\ &=&\displaystyle \int_{a_1}^{b_1} \left(\int_{a_2}^{b_2} f(x,y) \,dy \right) \,dx \end{array}
多重積分はこのような形で計算できる
\begin{array}{llllll} \displaystyle \displaystyle\int_{-\infty}^{\infty} e^{-x^2} \,dx\int_{-\infty}^{\infty} e^{-y^2} \,dy &=&\displaystyle\int_{-\infty}^{\infty} \left(\int_{-\infty}^{\infty} e^{-x^2} \,dx\right)e^{-y^2} \,dy \\ \\ &=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-x^2}e^{-y^2} \,dxdy \\ \\ &=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^2+y^2)} \,dxdy \end{array}
かなり怪しいですけど
とりあえずこの記事では
そういうことにしておいてください。
この辺りの詳細は長くなるので
重積分の記事でしっかりやります。
一応ざっくり説明するなら
「正で有界な普通の関数」だから OK みたいな
なんかそんな感じです。
ガウス積分の計算
ここまで飲み込めば後は作業
\begin{array}{llllll} \displaystyle x^2+y^2&=&r^2\cos^2θ+r^2\sin^2θ \\ \\ &=&r^2(\cos^2θ+\sin^2θ) \end{array}
\begin{array}{llllll} \displaystyle I&=&\displaystyle\int_{-\infty}^{\infty} e^{-x^2} \,dx \\ \\ \displaystyle I&=&\displaystyle\int_{-\infty}^{\infty} e^{-y^2} \,dy \end{array}
\begin{array}{llllll} \displaystyle I^2&=&\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^2+y^2)} \,dxdy \end{array}
\begin{array}{llllll} \displaystyle dxdy&=&rdθdr \end{array}
ゴールを目指して変形すると
\begin{array}{lllllll} \displaystyle \displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^2+y^2)} \,dxdy &=&\displaystyle\int_{0}^{2π}\int_{0}^{\infty} e^{-r^2} r\,drdθ \\ \\ &=&\displaystyle\int_{0}^{2π} \left( \int_{0}^{\infty} re^{-r^2} \,dr \right) \, dθ \end{array}
求めたいやつはこう
\begin{array}{llrllll} \displaystyle \frac{d}{dx}e^{-x^2}&=&\displaystyle -2xe^{-x^2} \\ \\ \displaystyle \frac{d}{dx}\left(-\frac{1}{2}e^{-x^2}\right)&=&\displaystyle xe^{-x^2} \end{array}
微分はこうで
\begin{array}{llllll} \displaystyle \lim_{x\to\infty} e^{-x^2} &=&0 \end{array}
定積分のとこはこうなので
\begin{array}{llllll} \displaystyle \displaystyle\int_{0}^{2π} \left( \int_{0}^{\infty} e^{-r^2} r\,dr \right) \, dθ&=&\displaystyle\int_{0}^{2π} \left( \left[ -\frac{1}{2}e^{-r^2} \right]_{0}^{\infty} \right) \, dθ \\ \\ &=&\displaystyle\int_{0}^{2π} \left( 0-\left(-\frac{1}{2}e^{-0^2}\right) \right) \, dθ \\ \\ &=&\displaystyle\int_{0}^{2π} \frac{1}{2} \, dθ \\ \\ \\ &=&\displaystyle\frac{1}{2}\displaystyle\int_{0}^{2π} \left( \frac{d}{dθ}θ \right) \, dθ \\ \\ &=&\displaystyle\frac{1}{2}\displaystyle \Bigl[ θ \Bigr]_{0}^{2π} \\ \\ &=& π\end{array}
I^2 はこう
そして最後
e^{-x^2} が「全区間で正」であることから
\begin{array}{llrllll} \displaystyle I^2&=&π \\ \\ I&=&\displaystyle\sqrt{π} &&\Bigl( I>0 \Bigr) \end{array}
I は正の値になる
\begin{array}{llllll} \displaystyle \int_{-\infty}^{\infty} e^{-x^2} \, dx &=&\displaystyle\sqrt{π} \end{array}
ということは
ガウス積分の値はこうなる。
とまあこんな感じに
かなり複雑な手順でしたが
このような流れでこれは求められます。
ちなみに e^{-ax^2} については
同様の手順で置換積分を行ってみれば
\begin{array}{llrllll} \displaystyle \frac{d}{dx}e^{-ax^2}&=&\displaystyle -2axe^{-ax^2} \\ \\ \displaystyle \frac{d}{dx}\left( -\frac{1}{2a}e^{-ax^2}\right)&=&\displaystyle xe^{-ax^2} \end{array}
\begin{array}{llrllll} \displaystyle\int_{0}^{2π} \left( \int_{0}^{\infty} e^{-ar^2} r\,dr \right) \, dθ&=&\displaystyle \frac{π}{a} \\ \\ \displaystyle \int_{-\infty}^{\infty} e^{-ax^2} \,dx &=&\displaystyle \sqrt{\frac{π}{a}} \end{array}
こうなることが分かります。
