|| ちゃんと足し算ができる集合のこと
『測度』を定義できる族 σ のこと
(族は集合を要素に持つ集合のこと)
スポンサーリンク
↓ の形で紹介されてるのをよく見ます。
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
3 つ目の A_n∈σ これは
\begin{array}{llllll} \displaystyle A_1,A_2,...,A_n,...∈σ \\ \\ A_1∈σ∧A_2∈σ∧\cdots∧A_n∈σ∧\cdots \end{array}
正確にはこうなんですが
\begin{array}{llllll} \displaystyle 1,2,3,4,5,...&\to&n \\ \\ A_1,A_2,A_3,...&\to&A_n \end{array}
見やすさのためにこのように省略しています。
関連
集合論「数学における基礎となるもの」
測度論「長さとか面積とかを厳密に定義」
ルベーグ測度「だいたいカバーできてる測度」
確率空間「確率について厳密に定義」
この記事は
ちょっとよく分からないと思います。
完全加法族 Completely Additive
|| 足し算が確実にできるとは
これは図形で見ると本当にそのままです。
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
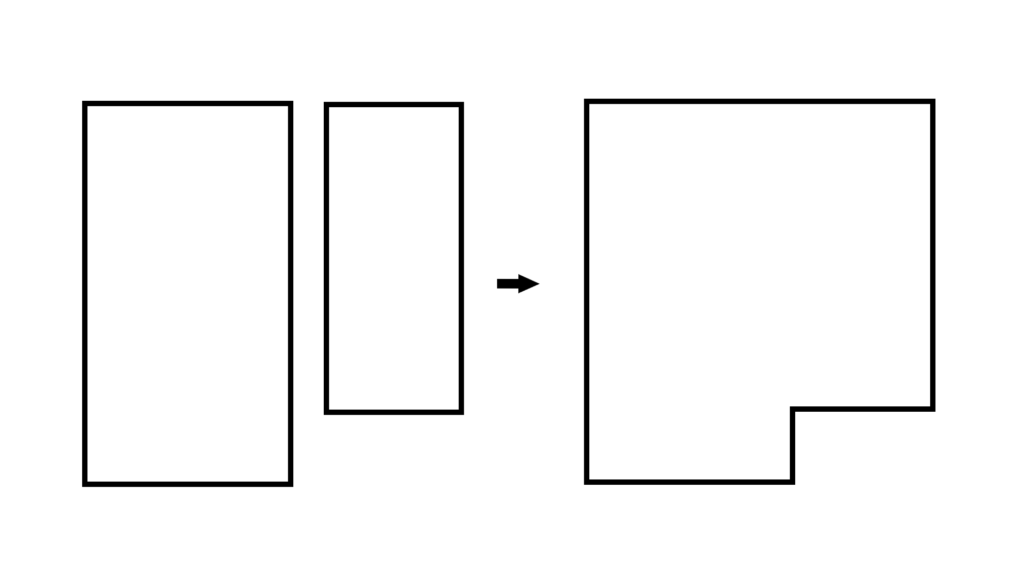
\begin{array}{cccccccc} \displaystyle A∩B≠∅ &&\to&&\left( \begin{array}{lclllll} \displaystyle A+B&× \\ \\ A⊂B &△ \\ \\ A,B⊂S &〇\end{array} \right) \\ \\ \\ \\ \displaystyle A∩B=∅ &&\to&&\left( \begin{array}{lclllll} \displaystyle A+B&〇 \\ \\ A⊂B &×\\ \\ A,B⊂S &〇 \end{array} \right) \end{array}
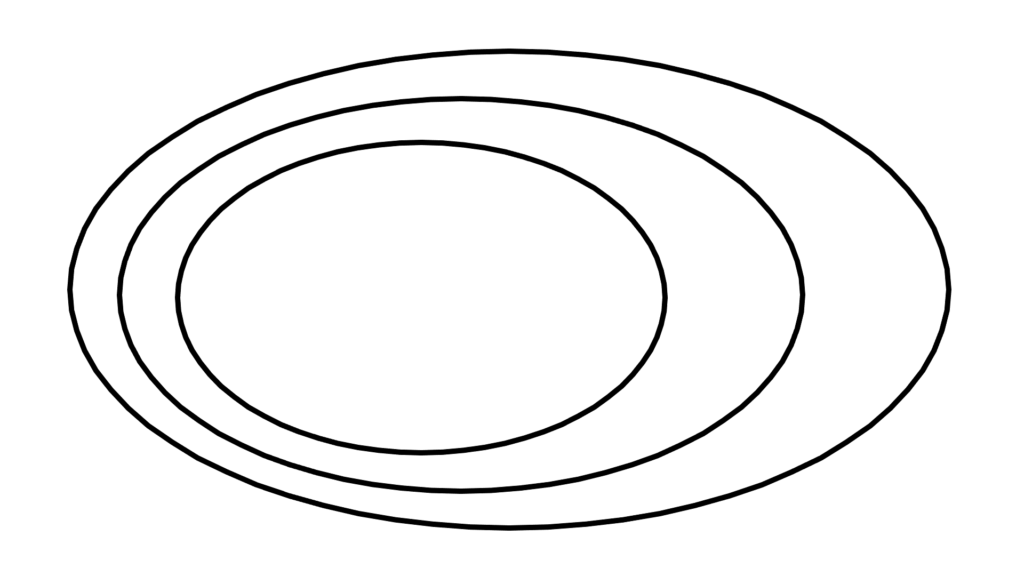
「測度論の核(成果)」と言って良いもので
単に「加法族」「 σ-加法族」とも言われます。
補足しておくと
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ S∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A,B∈σ&\to&\displaystyle A\setminus B∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n ∈σ \end{array} \right) \end{array}
完全加法族の実態はこんな感じです。
具体的な感じ
実際に使われるやつはもっと複雑ですが
\begin{array}{ccccllllll} \displaystyle \{∅,[0,\infty]\} &&〇 \\ \\ \displaystyle \{∅,[0,1),[0,\infty]\} &&× \\ \\ \displaystyle \{∅,[0,1),[1,\infty],[0,\infty]\} &&〇 \end{array}
\begin{array}{ccccllllll} \displaystyle \Bigl\{ ∅,\{a\},\{b\},\{c\} ,\{a,b,c\} \Bigr\} &&× \\ \\ \displaystyle \Bigl\{ ∅,\{a\},\{b\},\{c\} ,\{a,b\},\{b,c\},\{c,a\},\{a,b,c\} \Bigr\} && 〇 \end{array}
具体的には
こんな感じのやつが「完全加法族」になります。
補足しておくと
「可測集合」は「完全加法族の定義」を満たします。
完全加法族の役割
「微分積分学」における『積分』で矛盾が出ない。
「確率論」における『確率』を問題なく求められる。
\begin{array}{cccccccc} \displaystyle A∩B≠∅ &&\to&&\left( \begin{array}{lclllll} \displaystyle A+B&× \\ \\ A⊂B &△ \\ \\ A,B⊂S &〇\end{array} \right) \\ \\ \\ \displaystyle A∩B=∅ &&\to&&\left( \begin{array}{lclllll} \displaystyle A+B&〇 \\ \\ A⊂B &×\\ \\ A,B⊂S &〇 \end{array} \right) \end{array}
主にこれらを保証しているのが
この「完全加法族」で
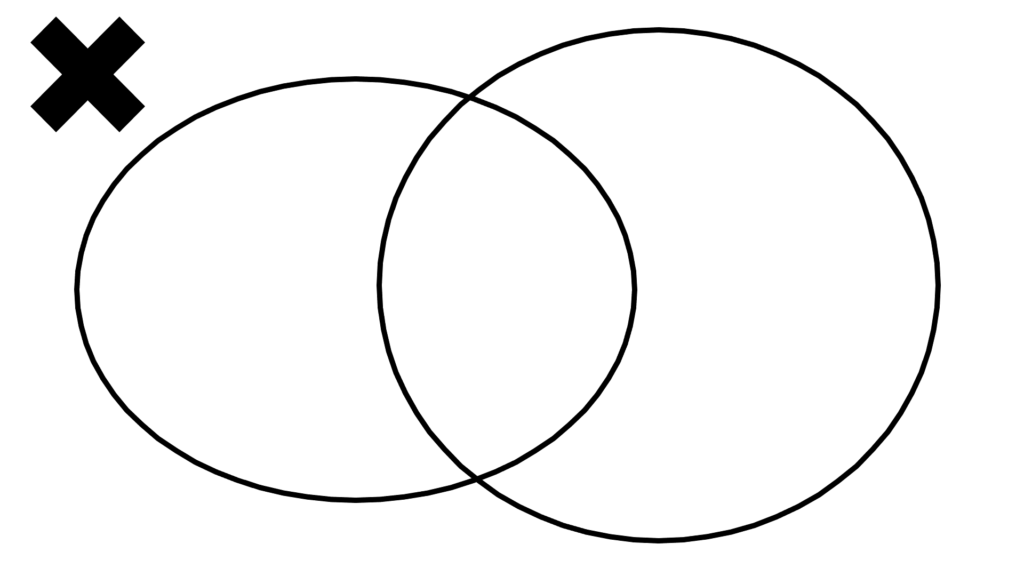
\begin{array}{llllll} \displaystyle \left( \begin{array}{cllllll} \displaystyle A∩B≠∅ \\ \\ μ(A)=1 \\ \\ μ(B)=1 \end{array} \right) &\to&μ(A)+μ(B)=2&? \end{array}
\begin{array}{llllll} \displaystyle A&⊂&B &&? \\ \\ B&⊂&A &&? \end{array}
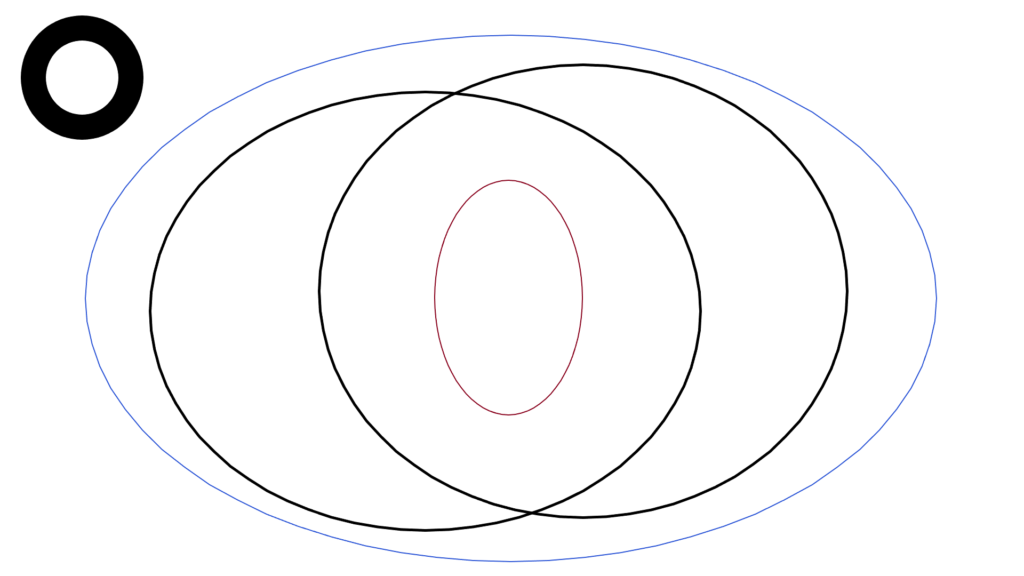
その役割は名前の通り
「足し算の無矛盾」を保証しています。
この役割から
\begin{array}{llllll} \displaystyle \left( \begin{array}{cllllll} \displaystyle A∩B=∅ \\ \\ μ(A)=1 \\ \\ μ(B)=1 \end{array} \right) &\to&μ(A)+μ(B)=2 \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{cllllll} \displaystyle i≠j &→& D_i∩D_j≠∅ \\ \\ \displaystyle D&=&\displaystyle\bigcup_{n=1}^{\infty}D_n \end{array} \right) &\to& \displaystyle \sum_{n=1}^{\infty}μ(D_n)=μ(D) \end{array}
この性質には
「完全加法性」なんて名前がついていたりします。
ルベーグ外測度と完全加法性
これを意識するのは
だいたい「ルベーグ外測度」を考える時で
\begin{array}{llllll} \displaystyle \sum_{n=1}^{\infty}μ(D_n)&\textcolor{pink}{≥}&μ(D) \end{array}
このように
「ルベーグ外測度」では
\begin{array}{llllll} \displaystyle D&=&D_1∪D_2∪D_3∪\cdots \end{array}
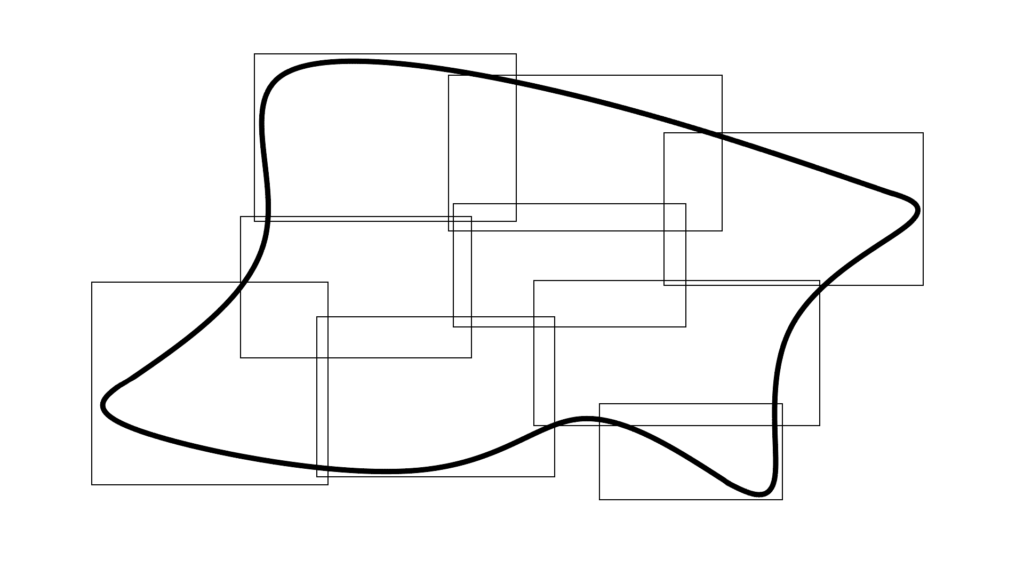
「全体の一部をカバーする図形」がたくさんあって

そうなると
中には『一部が重なってるもの』や
『図形からはみ出るもの』がありますから
\begin{array}{cllllll} \displaystyle i≠j &→& D_i∩D_j≠∅ \\ \\ \displaystyle D&=&\displaystyle\bigcup_{n=1}^{\infty}D_n \end{array}
図形 D と一致させるためには
この「互いに素」という性質が必須
重なってる部分
つまり余分な面積を 0 に近付けるために
\begin{array}{ccc} \displaystyle D&=&D_1∪D_2∪D_3∪\cdots \\ \\ μ^*(D)&=&μ(D_1∪D_2∪D_3∪\cdots) \\ \\ && μ(D_1∪D_2∪D_3∪\cdots)&\textcolor{pink}{≤}&μ(D_1)+μ(D_2)+\cdots \end{array}
一般的にはこうなるところを
\begin{array}{llllll} \displaystyle μ(D_1∪D_2∪D_3∪\cdots)&\textcolor{pink}{=}&μ(D_1)+μ(D_2)+\cdots \end{array}
このようにするので
「ルベーグ測度」では
こういうところで「完全加法性」を意識することになります。
定義が実現すること
「完全加法族」の定義だけ出されても
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
実は完全加法族について
きちんと知ることはできません。
\begin{array}{llllll} \displaystyle S∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A,B∈σ &\to&\displaystyle A\setminus B ∈σ \end{array}
\begin{array}{llllll} \displaystyle A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\textcolor{pink}{k}}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\textcolor{pink}{k}}A_n ∈σ \end{array}
というのも
完全加法族にはこういった性質も要求されていて
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
『必要最低限に絞り込めたもの』だけではなく
\begin{array}{llllll} \displaystyle S∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A,B∈σ &\to&\displaystyle A\setminus B ∈σ \\ \\ \\ \displaystyle A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\textcolor{pink}{k}}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\textcolor{pink}{k}}A_n ∈σ \end{array}
実際には
これらの性質も知っておく必要があるんです。
「完全加法族であるかどうか」の判定
その1点において ↓ は非常に有用ですが
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
『完全加法族とは何か』を知る上では
これはあまりにも情報不足
完全加法族が持つべき性質
完全加法族の全体像について
\begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array}
この定義から確認していくと
まず A_k の中身には
「同じではないという縛りが無い」ことから
\begin{array}{llllll} \displaystyle A_k&=&A_{k+1}&=&A_{k+1}&=&\cdots \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \end{array} \right) &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \end{array}
ちょっと変な工夫ではありますが
有限和に関してはこんな感じで
\begin{array}{llllll} \displaystyle ∅^c&=&S \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \end{array} \right)&\to&S∈σ \end{array}
全体を表す集合 S についてはこう
\begin{array}{llllll} \displaystyle (A∩B)^c&=&A^c ∪ B^c \\ \\ \displaystyle\left( \bigcap_{n=1}^{\infty}A_n \right)^c&=&\displaystyle\bigcup_{n=1}^{\infty}A_n^c \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} A∈σ &\to&A^c ∈σ\\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \end{array} \right)&\to&\displaystyle \left( \begin{array}{cllllll} \displaystyle\bigcup_{n=1}^{\infty}A_n^c∈σ \\ \\ ↓ \\ \\ \displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
\begin{array}{llllll} \displaystyle A_k&=&A_{k+1}&=&A_{k+1}&=&\cdots \end{array}
\begin{array}{llllll} \displaystyle\bigcap_{n=1}^{\infty}A_n∈σ&&\to&&\displaystyle\bigcap_{n=1}^{k}A_n∈σ \end{array}
共通部分はこんな感じで
\begin{array}{cccclccccll} \displaystyle A\setminus B&=&A∩B^c \end{array}
\begin{array}{llllll} \displaystyle \left( \begin{array}{llllll} A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n∈σ \end{array} \right)&\to&\displaystyle A\setminus B∈σ \end{array}
最後、差集合については
共通部分からすぐに導かれます。
以上
完全加法族は上記の操作を保証しているので
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ S∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A,B∈σ&\to&\displaystyle A\setminus B∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{k}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{\infty}A_n ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcap_{n=1}^{k}A_n ∈σ \end{array} \right) \end{array}
完全加法族とは何ぞやって話になるなら
こっちの方が表現としては適切かもしれません。
