|| 近似図形の測度論的な解釈
「区間(直線)」で表現される図形
スポンサーリンク
目次
測度論「図形を集合で厳密に扱う」
集合「点の集まりとして図形も表現できる」
集合族「この記事では図形の集まり」
区間「長さを求められる最も単純な図形」
区間塊「区間の集まりで表現される図形」
長さ「点の間隔を意味する正の実数」
完全加法的集合関数「扱いやすい関数のこと」
直積「次元を上げる感覚を意味する自然な操作」
集合環「かなりシンプルで抽象的な縛りがある集合族」
集合体「集合環より少しだけ縛りがきつい集合族」
完全加法族「集合の基本操作が全部できる集合族」
測度 Measure
|| 個数とか長さとか面積とかの総称
「完全加法族」上で定義されるもので
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr) &=& b-a \end{array}
矛盾が出ないように調整されています。
集合 Set
|| いろんなものを定義できる便利な最小単位
「数学(人が扱う理論)」の最小単位
\begin{array}{ccc} \mathrm{Elements} && \mathrm{Set} \\ \\ \\ 0,a &\in& \{0,a\} \\ \\ &\in& \{\} \\ \\ 0,1,2,3,4,5,... &\in& N \\ \\ 0,...,1 &\in&[0,1] \\ \\ \mathrm{apple},\mathrm{orange},... &\in &\mathrm{List} \\ \\ \mathrm{thing},\mathrm{space},... &\in& \mathrm{Concept} \end{array}
この記事では
「区間」「集合族」を定義する時に使われてます。
非交和 Disjoint
測度の話ではよく見るので
念のため紹介しておくと
\begin{array}{rcc} A,B∈σ &∧& \begin{array}{c} A∩B=∅ \end{array} \\ \\ \\ \\ A_1,A_2,A_3,...∈σ &∧& \begin{array}{c} i≠j \\ \\ ↓ \\ \\ A_i∩A_j=∅ \end{array} \end{array}
\mathrm{disjoint} の意味するところは
こういうことであるとしておきます。
(分かりやすく記述を省略するため)
集合族 Set of Sets
|| 集合を要素に持つ集合のこと
「環」「体」「完全加法族」で意識するやつ
\begin{array}{ccc} \displaystyle \{\} &⊂& \{ a,b,c \} \\ \\ \{a\} &⊂& \{ a,b,c \} \\ \\ \{a,b\} &⊂& \{ a,b,c \} \\ \\ \{a,b,c\} &⊂& \{ a,b,c \}\end{array}
\begin{array}{llllll} \displaystyle \mathrm{Set}_{\mathrm{Sets}}&=&\displaystyle \Bigl\{ \{\},\{a\},\{b\}, \{a,b\} \Bigr\} \end{array}
だいたい「冪集合(部分集合の集まり)」の
「部分集合」のことを指します。
集合族と空集合
「集合族」は「集合を要素に持つ集合」のことで
「空集合」は「要素を持たない集合」のことです。
\begin{array}{ccc} \displaystyle \mathrm{Set}_{\mathrm{Sets}}&=&\{\mathrm{Set}\} \\ \\ \mathrm{Set}_{\mathrm{Sets}}&≠&\{\} \end{array}
なのでこの定義に則って
「空集合」は「集合族」ではないとします。
(空の集合族は一応定義できる)
区間 Interval
|| 分かりやすいシンプルな図形
「長さ」とかの単位になる集合のこと
\begin{array}{ccl} \displaystyle (a,b)&=&\{ x∈R \mid a<x<b \} \\ \\ [a,b]&=&\{ x∈R \mid a≤x≤b \} \\ \\ \\ [a,b)&=&\{ x∈R \mid a≤x<b \} \\ \\ (a,b]&=&\{ x∈R \mid a<x≤b \} \end{array}
「位相幾何学」「測度論」の基礎的な概念で
主に「連続」の構造を扱う時に使われます。
測度や代数学から考える区間の定義
この「区間」という概念には
いろんな定義のやり方があります。
\begin{array}{llllll} \displaystyle \mathrm{Interval}_{\mathrm{unit}}&=&\{ [a,b)⊂R \mid -\infty< a≤b <\infty \} \end{array}
その中でも「長さを測れる」ものとして
こういった「集合族 \mathrm{Interval}_{\mathrm{unit}} 」が考えられて
(厳密にはこれだけが区間で基本集合の定義はこれ)
\begin{array}{ccc} \displaystyle [a,b) &∈& \mathrm{Interval}_{\mathrm{unit}} \\ \\ (a,b) &\not\in& \mathrm{Interval}_{\mathrm{unit}} \\ \\ [a,b] &\not\in& \mathrm{Interval}_{\mathrm{unit}} \\ \\ (a,b] &\not\in& \mathrm{Interval}_{\mathrm{unit}} \end{array}
「代数学」的な感覚で話を進める場合
まずこの対象からスタートすることで
中身の性質を調べたりします。
空集合を含めたい
「区間の最小限の構造」にあたる ↓ は
\begin{array}{llllll} \displaystyle \mathrm{Interval}_{\mathrm{unit}}&=&\displaystyle \left\{ [a,b)⊂R \, \middle| \, -\infty< a≤b <\infty \right\} \end{array}
↓ のように定義しても良さそうですが
\begin{array}{llllll} \displaystyle \mathrm{Interval}_{\mathrm{unit}}&=&\{ [a,b)⊂R \mid -\infty< a\textcolor{pink}{<}b <\infty \} \end{array}
このように定義する場合
この定義から「空集合」を生成できないため
\mathrm{Interval}_{\mathrm{unit}} の中に空集合を含めることができません。
空集合を含むといろんな操作を保証できる
確認しておくと
\begin{array}{ccc} ∅&⊂&A \\ \\ ∅ &=&A∩A^c \\ \\ ∅ &=&A\setminus A \end{array}
「最小の部分集合」「共通部分」
「差集合」「補集合」など
「空集合」を含めない場合
\begin{array}{lcc} \displaystyle A\setminus A&=&∅ \\ \\ A∩B&=&∅ \end{array}
「共通部分」「差集合」
少なくともこの辺りは
「区間」について閉じていない操作になります。
空集合を含む最低限の要件
しかし「空集合」を含む場合
その操作に関して「閉じている」
という状態を作れるので
\begin{array}{llllll} \displaystyle \mathrm{Interval}_{\mathrm{unit}}&=&\{ [a,b)⊂R \mid -\infty< a≤b <\infty \} \end{array}
a≥b という空集合になる条件の内
\begin{array}{ccccc} a<b &&→&&a≤b \end{array}
a<b の大小関係を一定に保てる
a=b のパターンを含むようにし
「空集合」を生成できるようにしています。
無限区間はまだ考えない
これを定義する上で
a+ε=-\infty,b=\infty を許すなら
\begin{array}{rlllll} \displaystyle [0,\infty)&⊂&R \\ \\ (-\infty,0)&⊂&R \end{array}
このような
「無限」を含む「無限区間」が考えられますが
\begin{array}{llllll} \displaystyle μ\Bigl( [0,\infty) \Bigr)-μ\Bigl( [1,\infty) \Bigr) \end{array}
「長さ」なんかを考える時
こういった「不定形」が考えられたりするので
これは定義の初期段階では考えないことにします。
区間塊 Figure
|| 区間の集まりで表現可能な図形のこと
ピクセルなんかで表現されてる図形の原型
\begin{array}{llllll} \displaystyle I_n&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle \mathrm{Figure}&=&\displaystyle \left\{ \bigcup_{n=1}^{k}I_n \, \middle| \, \mathrm{disjoint} → \bigcup_{n=1}^{k}I_n \right\} \end{array}
「ルベーグ外測度」の中身になる
「基本集合の集まり」として定義される集合族のこと
\begin{array}{llllll} \displaystyle A∩B=∅ &&→&& \begin{array}{llllll} A∪B \not\in \mathrm{Interval}_{\mathrm{unit}} \\ \\ A∪B \in \mathrm{Figure} \end{array} \\ \\ \\ A∩B≠∅ &&→&& \begin{array}{llllll} A∪B \in \mathrm{Interval}_{\mathrm{unit}} \\ \\ A∪B \in \mathrm{Figure} \end{array} \end{array}
これは
「区間(最小限)」ではない
「離れたやつの和集合」なども含む
\begin{array}{ccc} \displaystyle [0,1)∪[2,3) &\in& \mathrm{Figure} \\ \\ [a,b) &\in& \mathrm{Figure} \end{array}
より「直感的な区間」に近い概念になります。
区間塊の定義と完全加法性
↓ のような性質を
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
「完全加法性」と言うんですが
見てわかる通り
実は「区間塊」の定義はこれに由来していて
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→&\displaystyle \bigcup_{n=1}^{k}I_n \end{array}
この性質を緩めた「有限加法性」の形で
\displaystyle \bigcup_{n=1}^{k}I_n
この形の集合の存在は保証されています。
無限和の存在
極限の定義や
上限や下限の存在
以下のような等比級数の存在から
\begin{array}{llllll} \displaystyle S&=& \displaystyle\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots \\ \\ \displaystyle\frac{1}{2}S&=&\displaystyle\frac{1}{4}+\frac{1}{8}+\cdots \end{array}
\begin{array}{llllll} \displaystyle 1&=&\displaystyle\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots \end{array}
↓ のような
\begin{array}{llllll} \displaystyle \left[ 0,\frac{1}{2} \right) ∪ \left[ \frac{1}{2},\frac{1}{2}+\frac{1}{4} \right) ∪ \cdots &=& [0,1) \end{array}
「無限和」の存在が導かれますが
「全ての無限和」でこれが成立するとは限らないため
「区間塊」は「有限加法」の形で定義されています。
完全加法性と有限加法性
「完全加法性」を満たす場合
実は以下のような工夫を行えば
\begin{array}{llllll} ∅ &=& \displaystyle ∅∪∅∪\cdots \\ \\ ∅&=& \displaystyle I_{k+1}=I_{k+2}=I_{k+3}=\cdots \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}I_n &=&\displaystyle \left( \bigcup_{n=1}^{k}I_n \right) ∪ \left( \displaystyle \bigcup_{n=k+1}^{\infty}I_n \right) \\ \\ &=& \displaystyle \bigcup_{n=1}^{k}I_n \end{array}
これは「非交和 \mathrm{disjoint} 」の条件を満たすので
「有限加法性」もまた満たされます。
(有限加法性の方が条件としては緩い)
区間で生成できるいろんなもの
この「区間塊 \mathrm{Figure} 」という概念は
当然の帰結として「区間(最小限)」も含むため
\begin{array}{llllll} \displaystyle [a,b)&=&[a,b)∪∅∪∅∪\cdots \end{array}
\begin{array}{llllll} [a,b) &\in& \mathrm{Figure} \end{array}
「区間の定義(最低限)」もそうですが
「区間」と混同してしまいがちな概念になります。
\begin{array}{ccc} \displaystyle [a,b)∪[b+ε,c)&\in& \mathrm{Figure} \end{array}
実際
この「区間塊(基本集合)」という概念は
「直感的な意味」での「区間」をも意味するので
\begin{array}{ccc} [a,b)&\in& \mathrm{Figure} \end{array}
「区間」という記述がある場合
この意味で使われることはそれなりに多いです。
区間塊と非交和
単純な場合分けを行った時
\begin{array}{llllll} I_{ab}&=&\{ [a,b)⊂R \mid -\infty< a≤b <\infty \} \\ \\ I_{cd}&=&\{ [c,d)⊂R \mid -\infty< c≤d <\infty \} \end{array}
非交和にならない
\begin{array}{llllll} &&a&≤&c&<&b&≤&d \\ \\ c&≤&a&<&d&≤&b \\ \\ \end{array}
このパターンでは
I_{ab} と I_{cd} の「和集合」は
「区間(最低限)」になりますが
以下のパターンでは
\begin{array}{llllll} && a≤b &≤& c≤d \\ \\ c≤d &≤& a≤b \end{array}
I_{ab} と I_{cd} という区間は非交和になり
「区間(最低限)」の条件を満たしません。
( b=c,d=a の場合は満たす)
しかし「区間塊」は
これを含むよう定義されているので
\begin{array}{llllll} \displaystyle A∩B=∅ &&→&& \begin{array}{llllll} A∪B \not\in \mathrm{Interval}_{\mathrm{unit}} \\ \\ A∪B \in \mathrm{Figure} \end{array} \\ \\ \\ A∩B≠∅ &&→&& \begin{array}{llllll} A∪B \in \mathrm{Interval}_{\mathrm{unit}} \\ \\ A∪B \in \mathrm{Figure} \end{array} \end{array}
「区間塊」は「区間(最小限)」より
広い範囲をカバーする集合族であると言えます。
(区間塊は有限回の和集合操作について閉じている)
開区間や閉区間
これらもまた含めたい
そんな感じもありますが
\begin{array}{ccc} \displaystyle (a,b) & \not\in & \mathrm{Figure} \\ \\ [a,b] & \not\in & \mathrm{Figure} \end{array}
実は「区間塊」の中にこれらは含まれません。
(最小は含む 最大は含まない これが確定してる)
\begin{array}{llllll} \displaystyle I_n&=&[a_n,b_n) \\ \\ \mathrm{Left}&=&\{a_1,a_2,a_3,...,a_k\} \\ \\ \mathrm{Right}&=&\{b_1,b_2,b_3,...,b_k\} \end{array}
\begin{array}{llllll} \displaystyle \inf (\mathrm{Left})&=&a_{\mathrm{inf}} \\ \\ \sup(\mathrm{Right}) &=&b_{\mathrm{sup}} \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{k}I_n&=&\displaystyle \textcolor{pink}{[}a_\mathrm{\mathrm{inf}},b_i) ∪ \cdots ∪ [a_j,b_{\mathrm{sup}} \textcolor{pink}{)} \end{array}
それで良いのかって感じですが
実はそれでも良くて
というのも
「測度論」の考え方では
「長さ」は ↓ のように測られるので
\begin{array}{rcl} \displaystyle [a,b) &⊂& [a,b] &⊂& [a,b+ε) \\ \\ [a-ε,b) &⊂& (a,b) &⊂& [a,b) \end{array}
「区間塊の長さ」さえ厳密に定まっていれば
\begin{array}{llllll} \displaystyle μ \Bigl( [a,b) \Bigr) =b-a &&→&& \begin{array}{llllll} \displaystyle (a,b) &b-a \\ \\ [a,b] &b-a \end{array} \end{array}
他は間接的に求めることができる。
つまり、最小限のものを定義したいなら
「開区間・閉区間」は必要不可欠じゃないんです。
(全部含むのはボレル集合族)
長さ Length
|| 2つの点の間隔を表す正の実数
だいたい「区間」に定義されます。
\begin{array}{ccc} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \\ \\ \mathrm{Len}\Bigl( [a,b) \Bigr)&=&b-a \\ \\ \Bigl| [a,b) \Bigr|&=&b-a \\ \\ \mathrm{vol}\Bigl( [a,b) \Bigr)&=&b-a \end{array}
他にも2点間のものとして
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle (x_1,y_1) \\ \\ (x_2,y_2) \end{array} &→&\displaystyle\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \end{array}
こんな感じに定義されたりもしますが
これは「三平方の定理」ですから
\begin{array}{llllll} \displaystyle\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}&=& \displaystyle\sqrt{μ^2\Bigl( [x_1,x_2) \Bigr)+μ^2\Bigl( [y_1,y_2) \Bigr)} \end{array}
これも「区間」で表現できます。
区間に定義される
「測度論」の考え方から
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
自然な形として
「長さ μ 」の基礎はこのように定義されています。
他にも ↓ のように定義されることもあるんですが
\begin{array}{llllll} \displaystyle μ\Bigl( (a,b] \Bigr)&=&b-a \end{array}
この辺りは完全に好みですね。
(自分は [0,1) が便利過ぎるので [) 派閥)
区間塊にも定義できる
またこれと同様に
「区間塊」を「区間」のような感じで扱えるよう
(非交和 \mathrm{disjoint} の条件はこれのため)
\begin{array}{llllll} \displaystyle μ^+\left( \bigcup_{n=1}^{k}I_n \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \\ \\ \displaystyle μ^+\left( I_1∪I_2 \right)&=&\displaystyle μ(I_1)+μ(I_2) \end{array}
似たような形で
「区間塊 \mathrm{Figure} 」にも
自然な形で「長さ μ^+ 」が定義できます。
具体的には
\begin{array}{llllll} μ^+\Bigl( [0,1) \Bigr)&=&\displaystyle μ\Bigl( [0,1) \Bigr) \\ \\ &=& (1-0) \\ \\ \\ \displaystyle μ^+\Bigl( [0,1)∪[2,3)∪[4,6) \Bigr)&=&\displaystyle μ\Bigl( [0,1) \Bigr)+μ\Bigl( [2,3) \Bigr)+μ\Bigl( [4,6) \Bigr) \\ \\ &=& (1-0)+(3-2)+(6-4) \end{array}
「区間塊の長さ」はこんな感じです。
(非交和でなければ右が大きくなる)
区間の長さと区間塊の長さ
「区間塊」は「区間」を含む上に
\begin{array}{llllll} \displaystyle [a,b)&∈&\mathrm{Interval}_{\mathrm{unit}} \\ \\ [a,b)∪∅∪∅∪\cdots &∈&\mathrm{Figure} \end{array}
\begin{array}{llllll} \mathrm{Interval}_{\mathrm{unit}}&⊂&\mathrm{Figure} \end{array}
「区間塊の長さ μ^+ 」は
\begin{array}{llllll} \displaystyle μ^+\Bigl( [a,b) \Bigr)&=&μ\Bigl( [a,b) \Bigr) \end{array}
「区間塊の長さ」の定義より
「区間の長さ μ 」と同じになります。
この感覚は「拡張」と呼ばれ
例えば「区間塊の長さ μ^+ 」は
「区間の長さ μ の拡張」になります。
基本集合とジョルダン測度
「基本集合 [a,b) 」の「長さ」
\begin{array}{llllll} \displaystyle μ(I)&=&\displaystyle μ\Bigl( [a,b) \Bigr) \\ \\ \displaystyle μ^+\left( \bigcup_{n=1}^{k}I_n \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
これは「ジョルダン測度」でも「ルベーグ測度」でも
「区間の長さ μ 」で定義されていて
この基礎を使って
\begin{array}{ccccc} \displaystyle \int_{a}^{b} f(x)\,dx &=&F(b)-F(a) \\ \\ && F(b)-F(a) &=&\displaystyle μ \left( \Bigl[F(a),F(b)\Bigr) \right) \end{array}
この「定積分」の形から
\begin{array}{llllll} \displaystyle S&=&\displaystyle \bigcup_{n=1}^{\infty} I_n \end{array}
\begin{array}{ccc} A&⊂&S \\ \\ μ_{\mathrm{Jordan}}(A)&=&\displaystyle \inf \Bigl( μ(S) \Bigr) \end{array}
「ジョルダン測度 μ_{\mathrm{Jordan}} 」は
このような形で定義されています。
(後述する完全加法性を用いて)
基本集合とルベーグ測度
そしてこれを拡張する形で
「ルベーグ外測度」は
\begin{array}{ccc} A&⊂& \displaystyle \bigcup_{n=1}^{\infty} I_n \\ \\ μ_{\mathrm{Lebesgue}}(A) &≤& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty} I_n \right) \end{array}
\begin{array}{llllll} \displaystyle μ^+\left( \bigcup_{n=1}^{\infty} I_n \right) &=& \displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
「区間の長さ μ 」の「拡張」である
「区間塊の長さ μ^+ 」で定義されていて
\begin{array}{llllll} \displaystyle μ_{\mathrm{Lebesgue}}(A) &=&\displaystyle \inf \left\{ \sum_{n=1}^{\infty}I_n \,\, \middle| \,\, A⊂\bigcup_{n=1}^{\infty} I_n \right\} \end{array}
見てわかる通り
いずれも最終的には
「区間の長さ μ 」に行き着くので
\begin{array}{lccccccc} μ_{\mathrm{Jordan}}(A) && → &&\displaystyle μ(S) \\ \\ μ_{\mathrm{Lebesgue}}(A) &→& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty} I_n \right) &→&\displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
基礎になるものとして
「基本集合」という概念は
「区間(最低限) [a,b) 」という形で定義されています。
完全加法的集合関数 σ-Additive
|| 完全加法性を持つ集合関数のこと
「長さ」「測度」なんかを意味する単語
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
「完全加法性」を満たす「集合関数」のことを
「完全加法的集合関数」と言います。
区間や区間塊の長さは完全加法的
確認は後に回すとして
\begin{array}{lllllllll} \displaystyle \mathrm{disjoint} &&→&& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) &=&\displaystyle \sum_{n=1}^{\infty}μ(I_n) \\ \\ \displaystyle \mathrm{disjoint} &&→&& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty} A_n \right) &=&\displaystyle \sum_{n=1}^{\infty}μ^+(A_n) \end{array}
「区間」や「区間塊」から
「長さ」を得る「集合関数 μ,μ^+ 」は
実は「完全加法的集合関数」になります。
直積 Product
|| 次元を自然に拡張する操作
「長方形」「直方体」の自然な定義
\begin{array}{ccl} \displaystyle \mathrm{Rectangle} &=&I_X \times I_Y \\ \\ \mathrm{Cuboid}&=&I_X \times I_Y \times I_Z \end{array}
「面積」や「体積」は以下のように
「区間の長さの掛け算」で表現されます。
\begin{array}{llllll} \displaystyle \Bigl| I_X \times I_Y \Bigr|&=&(b_x-a_x)(b_y-a_y) \\ \\ \Bigl| I_X \times I_Y \times I_Z \Bigr|&=&(b_x-a_x)(b_y-a_y)(b_z-a_z) \end{array}
この記事の本筋から逸れてしまうので
これの厳密な話は別の記事で。
集合環 Ring
|| 縛りがかなり緩い抽象的な構造
「空集合じゃない」「和集合」「差集合」
\begin{array}{llllll} \displaystyle \begin{array}{rrr} \displaystyle ∅&≠&\mathrm{Ring} \\ \\ A\setminus B&\in&\mathrm{Ring} \\ \\ A∪B&\in&\mathrm{Ring} \end{array} &&→&&\left(\begin{array}{rrr} \displaystyle ∅&∈&\mathrm{Ring} \\ \\ A∩ B&\in&\mathrm{Ring} \end{array}\right) \end{array}
この縛りのみで構成された「集合族」のこと
(足し算掛け算ができる集合を環と言う)
\begin{array}{ccccc} A\setminus B &&→&&(A^c∪B)^c \\ \\ \displaystyle \mathrm{Ring}&&←&&\mathrm{Field} \\ \\ \{∅\} && &&\{∅,X\} \\ \\ \{∅,\{a\}\} && && \{∅,\{a\},\{b\},\{a,b\}\} \end{array}
以下で紹介する「集合体」より縛りは緩いです。
(補集合 → 差集合 にして緩めている)
集合体 Field
|| 完全加法族より縛りが緩いやつ
「完全加法」→「有限加法」にして緩めたやつ
\begin{array}{rcr} && ∅∈\mathrm{Field} \\ \\ A∈\mathrm{Field} &→& A^c∈\mathrm{Field} \\ \\ A,B∈\mathrm{Field} &→& A∪B∈\mathrm{Field} \end{array}
「完全加法族」よりも縛りが緩くて
\begin{array}{ccc} \displaystyle\bigcup_{n=1}^{\infty}A_n \end{array}
「無限和」を含むかどうかは
強制ではなく任意になります。
完全加法族 σ-Additive
|| 集合の基本操作で生成される全てを持つ集合族
だいたいなんでもできる矛盾の無い便利な枠組み
\begin{array}{llllll} \displaystyle\left( \begin{array}{llllll} \displaystyle S≠∅ \\ \\ σ⊂2^S \\ \\ A^c = S\setminus A \end{array} \right) &\to& \displaystyle \left( \begin{array}{rllllll} \displaystyle ∅∈σ \\ \\ A∈σ &\to&A^c ∈σ \\ \\ A_n∈σ &\to&\displaystyle\bigcup_{n=1}^{\infty}A_n ∈σ\end{array} \right) \end{array}
「集合環」や「集合体」は
\begin{array}{ccc} \displaystyle \mathrm{Ring} &→&σ(\mathrm{Ring}) \\ \\ \{∅\} && \{∅,X\} \\ \\ \{∅,\{a\}\} && \{∅,\{a\},\{b\},\{a,b\}\} \\ \\ \\ \mathrm{Field} &→&σ(\mathrm{Field}) \\ \\ A\setminus B \,\, A^c && A\setminus B \,\, A^c \end{array}
いずれもこれの条件を緩めたものになります。
区間塊は集合環
結論からいくと
「集合環」の定義は ↓ で
\begin{array}{rrr} \displaystyle ∅&≠&\mathrm{Figure} \\ \\ A\setminus B&\in&\mathrm{Figure} \\ \\ A∪B&\in&\mathrm{Figure} \end{array}
「区間塊」はこの条件を満たします。
(区間は和集合のほとんどが条件を満たさない)
区間や区間塊の定義の確認
というわけで確認していくと
まず「区間」の定義が ↓
\begin{array}{llllll} \displaystyle \mathrm{Interval}_{\mathrm{unit}}&=&\{ [a,b)⊂R \mid -\infty< a≤b <\infty \} \end{array}
そして「区間塊」の定義が ↓ です。
\begin{array}{llllll} \displaystyle I_1,I_2,,...,I_n&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle \mathrm{Figure}&=&\displaystyle \left\{ \bigcup_{n=1}^{k}I_n \, \middle| \, \mathrm{disjoint} → \bigcup_{n=1}^{k}I_n \right\} \end{array}
それぞれ a,b を定めて I_n を定義すれば
要素となる集合を生成することができます。
区間塊と空集合
「要素を持たない集合(空集合)」は
「区間塊の要素」を持っていないため
\begin{array}{llllll} \displaystyle ∅&≠& \mathrm{Figure} \end{array}
「区間塊」の定義を満たしません。
(区間塊に該当する集合が存在すると解釈します)
区間塊と和集合
順番的には
先に「差集合」について確認したいですが
\begin{array}{llllll} \displaystyle A∪B&=&\{ e \mid e\in A ∨ e\in B \} \end{array}
\begin{array}{llllll} \displaystyle A∪B&∈&\mathrm{Figure} \end{array}
差集合について示す時
これが使えると楽なので
先にこちら側から説明していきます。
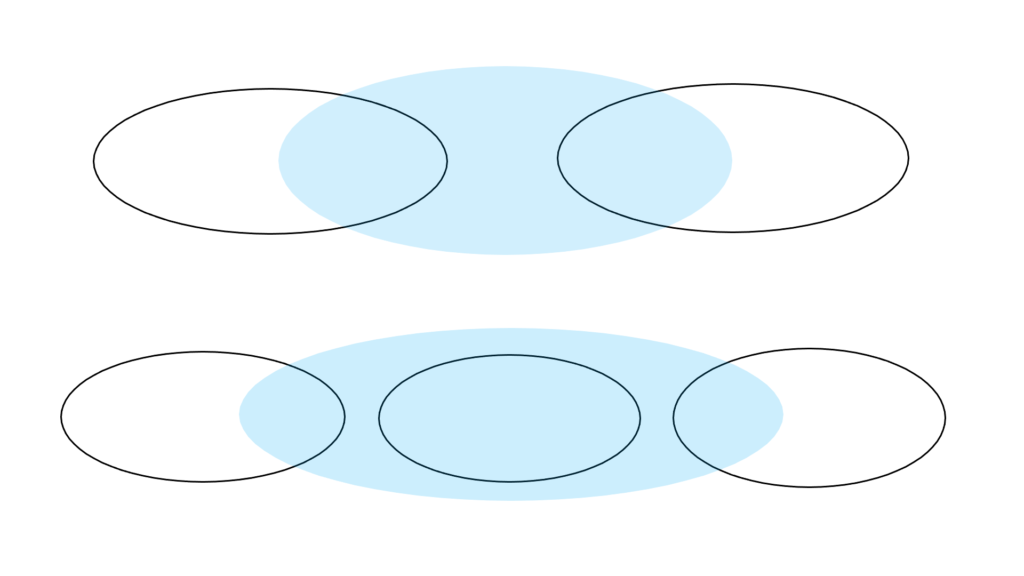
区間同士の和集合
「区間塊」の定義から分かる通り
\begin{array}{llllll} \displaystyle [a,b)∪[c,d) &∈&\mathrm{Figure} \end{array}
これはどのパターンであっても
\begin{array}{c} \displaystyle [a,b)∩[c,d)=∅ \\ \\ ↓ \\ \\ \begin{array}{llllll} \displaystyle a≤b<c≤d &&→&& [a,b)∪[c,d) &∈\mathrm{Figure} \\ \\ a≤b=c≤d &&→&& [a,b)∪[c,d)=[a,d) &∈\mathrm{Figure} \\ \\ \\ c≤d<a≤b &&→&& [a,b)∪[c,d) &∈\mathrm{Figure} \\ \\ c≤d=a≤b &&→&& [a,b)∪[c,d)=[c,b) &∈\mathrm{Figure} \end{array} \end{array}
確認してみれば
\begin{array}{c} \displaystyle [a,b)∩[c,d)≠∅ \\ \\ ↓ \\ \\ \begin{array}{llllll} \displaystyle a≤c≤b≤d &&→&& [a,b)∪[c,d)=[a,d) &∈\mathrm{Figure} \\ \\ a≤c≤d≤b &&→&& [a,b)∪[c,d)=[a,b) &∈\mathrm{Figure} \\ \\ \\ c≤a≤d≤b &&→&& [a,b)∪[c,d)=[c,b) &∈\mathrm{Figure} \\ \\ c≤a≤b≤d &&→&& [a,b)∪[c,d)=[c,d) &∈\mathrm{Figure} \end{array} \end{array}
確実に「区間塊」になるので
「区間同士の和集合」は
必ず「区間塊」になると言えます。
区間塊と区間の和集合
「区間塊と区間」の「和集合」については
「区間塊」と「区間 I_{k+1} 」が
「非交和 \mathrm{disjoint} 」であれば
\begin{array}{llllll} \displaystyle I_1,I_2,,...,I_k,I_{k+1}&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle \left( \bigcup_{n=1}^{k} I_n \right)∪I_{k+1} &=&\displaystyle \bigcup_{n=1}^{k+1} I_n \end{array}
「区間塊」の定義そのままなんですが
「非交和」とは限らないので
「非交和ではない」パターンではどうなるか
きちんと考える必要があります。
区間塊と非交和ではない区間の和集合
というわけで確認していくと
まず先ほど確認した通り
\begin{array}{llllll} \displaystyle I_1∪I_2 &&→&& \displaystyle \left\{ \begin{array}{llllll} \displaystyle I_u &&(I_1∩I_2≠∅) \\ \\ I_1∪I_2 &&(I_1∩I_2=∅) \end{array} \right. \end{array}
「区間同士の和集合」により生成されるのは
「区間」か「非交和な区間の和集合」で
特に「非交和じゃない」場合では
「共通する要素を持つ区間」の数に関係なく
その部分の和集合は「1つの区間」になります。
\begin{array}{llllll} \displaystyle I_1∪I_2 &→& \begin{array}{llllll} \displaystyle I_u &&(I_1∩I_2≠∅) \end{array} \end{array}
「非交和」という条件の元で
「1つの区間になる」パターンもありますが
\begin{array}{llllll} \displaystyle [a,b)∪[b,c)&=&[a,c) \end{array}
これは「区間塊の定義」において
特に問題にならないので
単に「非交和かどうか」で区別した上で
\begin{array}{rcc} \displaystyle A_1,A_2,,...,A_k&∈&\mathrm{Interval}_{\mathrm{unit}} \\ \\ B_1&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} A &=& \displaystyle \bigcup_{n=1}^{k} A_n \end{array}
\begin{array}{l} \{ A_n∈A \mid A_n∩B_1=∅ \}&=&P \\ \\ \{ A_n∈A \mid A_n∩B_1≠∅ \} &=&Q \end{array}
「区間塊と区間の和集合」を考えてみると
\begin{array}{llllll} F_1&=& \displaystyle \bigcup_{A_n∈Q}A_n \end{array}
\begin{array}{llllll} \displaystyle A&=&\displaystyle \left(\bigcup_{A_n∈P}A_n \right)∪\left(\bigcup_{A_n∈Q}A_n \right) \end{array}
「 B_1 と共通部分がある区間塊 F_1 」と
「共通部分が無い(非交和)区間塊」に分ける形で
「区間塊 A 」を再定義できるので
\begin{array}{llllll} \displaystyle F_1∪B_1&=& I_1 \end{array}
後はそのまま
生成された「非交和な区間の和集合」をとれば
\begin{array}{llllll} \displaystyle A∪B_1&=&\displaystyle \left(\bigcup_{A_n∈P}A_n \right)∪\left(\bigcup_{A_n∈Q}A_n \right)∪B_1 \\ \\ &=&\displaystyle \left(\bigcup_{A_n∈P}A_n \right)∪F_1∪B_1 \\ \\ &=&\displaystyle \left(\bigcup_{A_n∈P}A_n \right)∪I_1 \end{array}
\begin{array}{llllll} \mathrm{disjoint} &→&\displaystyle \left(\bigcup_{A_n∈P}A_n \right)∪I_1 \end{array}
これは確実に「区間塊」になるので
「区間塊と区間の和集合」は
「区間塊」になると言えます。
区間塊同士の和集合
これは ↑ の操作の繰り返しです。
\begin{array}{llllll} \displaystyle A_1,A_2,A_3,...,A_{a}&∈&\mathrm{Interval}_{\mathrm{unit}} \\ \\ B_1,B_2,B_3,...,B_{b}&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle A&=&\displaystyle \bigcup_{n=1}^{a} A_n \\ \\ B&=&\displaystyle \bigcup_{n=1}^{b} B_n \end{array}
「区間塊と区間の和集合」が
「区間塊」になることから
「片方の区間塊」の中身は変えず
\begin{array}{lcl} \displaystyle B_1 &=&A_{a+1} \\ \\ B_2 &=&A_{a+2} \\ \\ &\vdots \\ \\ B_b &=&A_{a+b} \end{array}
「名前」と「添え字」だけを書き換え
\begin{array}{llllll} \displaystyle \left( \bigcup_{n=1}^{k} A_n \right)∪A_{a+1} &=&\displaystyle \bigcup_{n=1}^{a+1} A_n &&∈\mathrm{Figure} \\ \\ \displaystyle \left( \bigcup_{n=1}^{k+1} A_n \right)∪A_{a+2} &=&\displaystyle \bigcup_{n=1}^{a+2} A_n &&∈\mathrm{Figure} \end{array}
「区間塊と区間の和集合」を繰り返しとることで
「区間塊と区間の和集合」の形を維持した上で
「区間塊同士の和集合」を構成できるので
\begin{array}{llllll} A∪B &=& \displaystyle \left( \bigcup_{n=1}^{a} A_n \right) ∪ \left( \bigcup_{n=1}^{b} B_n \right) \\ \\ &=&\displaystyle \left( \bigcup_{n=1}^{a} A_n \right) ∪ \left( \bigcup_{n=a+1}^{a+b} A_n \right) \\ \\ &=&\displaystyle \bigcup_{n=1}^{a+b} A_n \end{array}
「区間塊同士の和集合」は
「区間塊」になると言えます。
区間塊と差集合
確認しておくと
「差集合」というのは
\begin{array}{llllll} \displaystyle A\setminus B&=&\{ e \mid e\in A ∧ e\not\in B \} \\ \\ &=&\{ e \mid e\in A ∧ ¬(e\in B) \} \end{array}
\begin{array}{llllll} [0,2)\setminus [0,1)&=&[1,2) \end{array}
「集合 A の要素」の中から
「集合 B の要素を取り除く」操作で
「互いに素(非交和)」の場合では
\begin{array}{llllll} \mathrm{disjoint} &→& \displaystyle A\setminus B=A \end{array}
「取り除く要素が無い」ので
このパターンではなにも変化しない操作になります。
区間同士の差集合
「共通部分が無い」なら変化しませんが
「共通部分がある」場合
\begin{array}{llllll} \displaystyle A∩B&≠&∅ \end{array}
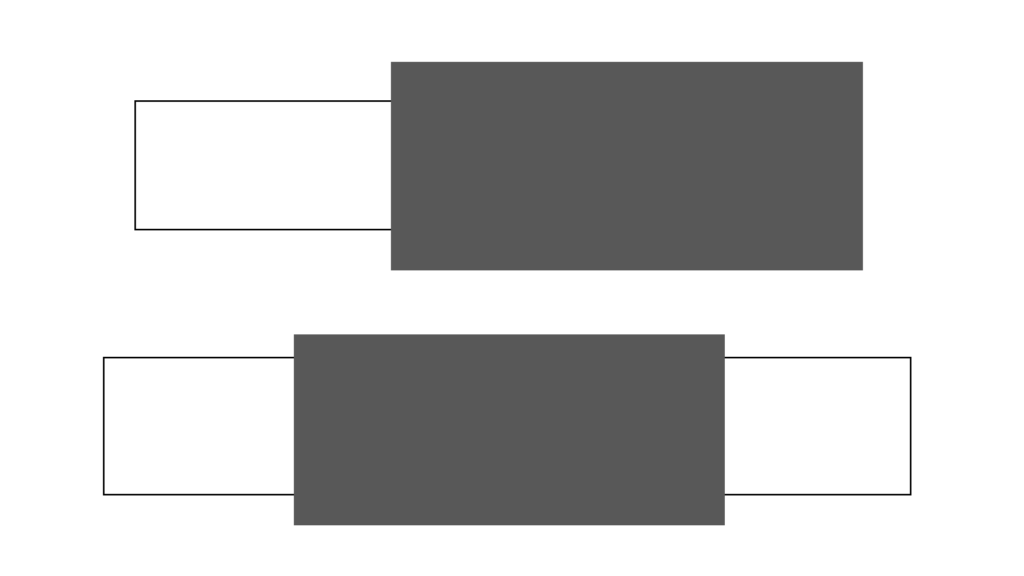
「2つの区間 A,B 」で考えると
B の要素が取り除かれた集合 A は
この2パターンのどちらかに変化し
\begin{array}{llllll} \displaystyle \begin{array}{llllll} \displaystyle [a,b),[c,d)&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array} \end{array}
\begin{array}{llllll} \displaystyle \begin{array}{lcccl} \displaystyle a≤c≤b≤d &&→&&[a,b) \setminus [c,d)=[a,c) \\ \\ c≤a≤d≤b &&→&&[a,b) \setminus [c,d)=[d,b) \end{array} \\ \\ \\ \begin{array}{lcccl} \displaystyle a≤c≤d≤b &&→&&[a,b) \setminus [c,d)=[a,c)∪[d,b) \\ \\ c≤a≤b≤d &&→&&[a,b) \setminus [c,d)=∅ \end{array} \end{array}
これらはいずれも「区間塊」になるので
\begin{array}{llllll} \displaystyle [a,b) \setminus [c,d) &∈&\mathrm{Figure} \end{array}
「区間」同士の「差集合」は
全てのパターンで「区間塊」になります。
区間塊と区間の差集合
これが分かれば後は楽
\begin{array}{llllll} \displaystyle A_1,A_2,A_3,...,A_{a}&∈&\mathrm{Interval}_{\mathrm{unit}} \\ \\ B_1,B_2,B_3,...,B_{b}&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle A\setminus B &∈&\mathrm{Figure} \end{array}
「区間塊」が「区間の集まり」である以上
\begin{array}{llllll} \displaystyle A&=&\displaystyle \bigcup_{n=1}^{a} A_n \\ \\ B&=&\displaystyle \bigcup_{n=1}^{b} B_n \end{array}
A から B_1 を取り除く
A から B_2 を取り除くという具合に
操作を分解していけば
\begin{array}{llllll} \displaystyle (P∪Q)\setminus R&=&\{ e \mid (e\in P ∨ e\in Q)∧e\not\in R \} \\ \\ &=& \{ e \mid (e\in P ∧e\not\in R )∨ (e\in Q∧e\not\in R) \} \\ \\ &=&(P\setminus R)∪(Q\setminus R) \end{array}
「区間 A_n 」に対して
「区間 B_1 の要素」を取り除くとすると
\begin{array}{llllll} A \setminus B_1 &=& \displaystyle \left(\bigcup_{n=1}^{a}A_n \right) \setminus B_1 \\ \\ &=&\displaystyle \left(\bigcup_{n=1}^{a}A_n\setminus B_1 \right) \end{array}
「区間同士の差集合」が「区間塊」になる
「区間塊同士の和集合」が「区間塊」になることから
\begin{array}{llllll} \displaystyle A\setminus B_1&∈&\mathrm{Figure} \end{array}
「区間塊から区間を引いた差集合」は
「区間塊」になると言えます。
区間塊と区間塊の差集合
↑ の事実より
\begin{array}{llllll} \displaystyle (A\setminus B)\setminus C &=&\{ e \mid (e\in A ∧ e\not\in B) ∧ e\not\in C \} \\ \\ &=&\{ e \mid e\in A ∧ e\not\in B ∧ e\not\in C \} \\ \\ &=&A\setminus B \setminus C \\ \\ \\ &=&\{ e \mid e\in A ∧ ¬(e\in B) ∧ ¬(e\in C) \} \\ \\ &=&\{ e \mid e\in A ∧ ¬(e\in B ∨ e\in C) \} \\ \\ \\ &=&A∩(B∪C)^c \\ \\ &=&A\setminus (B∪C) \end{array}
「集合演算」の定義から
「区間塊同士の差集合」もまた
\begin{array}{llllll} A\setminus (B_1∪B_2) &=& A \setminus B_1 \setminus B_2 \\ \\ &=& (A \setminus B_1) \setminus B_2 \\ \\ &=& \displaystyle \left( \left(\bigcup_{n=1}^{a}A_n \right) \setminus B_1 \right) \setminus B_2 \\ \\ &=&\displaystyle \left(\bigcup_{n=1}^{a}A_n \setminus B_1 \right) \setminus B_2 \\ \\ &=&\displaystyle \bigcup_{n=1}^{a}A_n \setminus B_1 \setminus B_2 \end{array}
これが「区間塊と区間 B_i の差集合」であり
確実に「区間塊」になることから
\begin{array}{lcc}\displaystyle \left(\bigcup_{n=1}^{a} A_n \right) \setminus (B_1)&∈& \mathrm{Figure} \\ \\ \displaystyle \left(\bigcup_{n=1}^{a} A_n \right) \setminus (B_1∪B_2)&∈& \mathrm{Figure} \\ \\ \displaystyle \left(\bigcup_{n=1}^{a} A_n \right) \setminus (B_1∪B_2∪B_3)&∈& \mathrm{Figure} \\ \\ &\vdots \\ \\ \displaystyle \left(\bigcup_{n=1}^{a} A_n \right) \setminus (B_1∪B_2∪\cdots ∪B_b)&∈& \mathrm{Figure} \end{array}
「区間塊による差集合」を
「区間 B_i との差集合の繰り返し」として考えると
\begin{array}{llllll} \displaystyle A_1,A_2,A_3,...,A_{a}&∈&\mathrm{Interval}_{\mathrm{unit}} \\ \\ B_1,B_2,B_3,...,B_{b}&∈&\mathrm{Interval}_{\mathrm{unit}} \end{array}
\begin{array}{llllll} \displaystyle A&=&\displaystyle \bigcup_{n=1}^{a} A_n \\ \\ B&=&\displaystyle \bigcup_{n=1}^{b} B_n \end{array}
\begin{array}{llllll} \displaystyle A\setminus B &∈&\mathrm{Figure} \end{array}
「区間塊同士の差集合」もまた
「区間塊」になると言えます。
区間塊の長さと完全加法的集合関数
とりあえず定義を確認しておくと
「完全加法的集合関数 μ 」の定義は ↓
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
「区間塊の長さ μ^+ 」は ↓
\begin{array}{llllll} F&=&\displaystyle\bigcup_{n=1}^{k}I_n \end{array}
\begin{array}{llllll} \mathrm{disjoint} &→& μ^+\left( F \right)=\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
「区間の長さ μ 」は ↓ です。
\begin{array}{llllll} \displaystyle μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
「区間・区間塊の長さ」
これらの定義はどちらも「有限」の範囲で
「無限」についての言及はされていません。
確定させておきたい前提
ゴールが「完全加法性」である
この事実を考えると
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
扱うことになる「区間」については
「非交和」を前提に話を進めたくなります。
そうすれば
「区間塊の長さ μ^+ 」を考える時
\begin{array}{llllll} \displaystyle μ^+\left( F \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
確実にこれが成立すると言えるので
話が簡単になりますから。
区間の長さは完全加法的集合関数である
これが意味するところは
つまりは「区間 I 」の「無限分割」が可能で
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
\begin{array}{llllll} \displaystyle I&=&\displaystyle \bigcup_{n=1}^{\infty} I_n \end{array}
これが成立するって話なので
これが成立するのかどうかを調べれば
「区間の長さ」が「完全加法的集合関数」かどうか
確認することができます。
条件を満たす区間の存在
「非交和」「区間になる」
この条件を満たす「区間」は
\begin{array}{llllll} \displaystyle [0,1)∪[1,2)&=&[0,2) \\ \\ [a,b)∪[b,c)&=&[a,c) \end{array}
「区間の和集合」について確認した通り
このような形だけ
\begin{array}{llllll} \displaystyle I&=&[a_1,a_k) \end{array}
\begin{array}{llllll} \displaystyle [a_1,a_k)&=&\displaystyle \bigcup_{n=1}^{k-1} [a_n,a_{n+1}) \end{array}
つまり「区間 I 」を「複数の区間に分割」する場合
絶対にこの形になります。
区間の無限和が区間になるような区間
以上の結果から
\begin{array}{rcl} \displaystyle \bigcup_{n=1}^{k-1} [a_n,a_{n+1}) &=&[a_1,a_{k}) \\ \\ \displaystyle \bigcup_{n=1}^{\infty} [a_n,a_{n+1}) &=&[a_1,a_{\infty}) \end{array}
このようになる「区間 [a_1,a_{\infty}) 」が
\begin{array}{llllll} \displaystyle μ\Bigl( [a_1,a_{\infty}) \Bigr)&=&a_{\infty}-a_1 \end{array}
「区間の長さ μ 」で値が求められる
「無限和(区間)」になります。
区間の無限和が区間になるような区間の存在
というわけで実際にそんなものがあるのか
条件を見ながら考えていくと
\begin{array}{llllll} \displaystyle 1&=&\displaystyle \frac{1}{2} + \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+\cdots \end{array}
例えばこのような等比級数の存在から
\begin{array}{llllll} \displaystyle \left[ 0,\frac{1}{2} \right)∪\left[ \frac{1}{2},\frac{1}{2}+\frac{1}{4} \right)∪\left[ \frac{1}{2}+\frac{1}{4},\frac{1}{2}+\frac{1}{4}+\frac{1}{8} \right)∪\cdots \end{array}
このような区間が考えられて
\begin{array}{lcrcl} \displaystyle \sum_{n=1}^{k}\frac{1}{2^n} &=& S \\ \\ && S &=&\displaystyle \frac{1}{2} + \frac{1}{4}+ \frac{1}{8}+\cdots+\frac{1}{2^k} \\ \\ && \displaystyle \frac{1}{2}S &=&\displaystyle \,\,\,\,\, \,\,\,\,\, \,\, \frac{1}{4}+ \frac{1}{8}+\cdots+\frac{1}{2^k}+\frac{1}{2^{k+1}} \end{array}
\begin{array}{rcrcc} \displaystyle S-\frac{1}{2}S&=&\displaystyle\frac{1}{2}S &=&\displaystyle\frac{1}{2}-\frac{1}{2^{k+1}} \\ \\ &&\displaystyle S &=&\displaystyle 1-\frac{1}{2^{k}} \end{array}
\begin{array}{llllll} \displaystyle \left[ 0,\sum_{n=1}^{k}\frac{1}{2^n} \right)&=&\displaystyle \left[ 0,1-\frac{1}{2^k} \right) \end{array}
この「区間」の「有限和」がこれであり
\begin{array}{llllll} \displaystyle \lim_{k\to\infty}\frac{1}{2^k} &=&0 \end{array}
「極限」の定義より
\begin{array}{ccc} \displaystyle \lim_{k\to\infty} μ\left( \left[ 0,1-\frac{1}{2^k} \right) \right)&=&\displaystyle \lim_{k\to\infty}\left( 1-\frac{1}{2^k} \right) \\ \\ &=&1-0 \\ \\ &=& μ \Bigl( [0,1) \Bigr) \end{array}
「無限和」は確実にこのようになることから
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
「完全加法性」の条件を満たす
「無限和の存在」が導かれます。
無限和と任意の区間の長さ
↑ が分かれば後は単純で
\begin{array}{llllll} \displaystyle \left[ 0,\sum_{n=1}^{k}\frac{1}{2^n} \right) \end{array}
「任意の実数 a 」と
「それに関わる実数 b(≥a) 」を使って
\begin{array}{llllll} \displaystyle \left[ 0,\sum_{n=1}^{k}\frac{1}{2^n} \right) &→&[a,b) \end{array}
この無限和の構成を考えれば
\begin{array}{llllll} \displaystyle \displaystyle \left[ 0,\sum_{n=1}^{k}\frac{1}{2^n} \right) &→&\displaystyle \left[ a,b\sum_{n=1}^{k}\frac{1}{2^n} \right) \\ \\ && \displaystyle \left[ a,b\sum_{n=1}^{k}\frac{1}{2^n} \right)&\overset{k\to\infty}{\to}&\displaystyle \left[ a,b \right) \end{array}
\begin{array}{llllll} & \displaystyle \left[ a,b\left(\frac{1}{2}\right) \right) \\ \\ ∪&\displaystyle\left[ b\left(\frac{1}{2}\right),b\left(\frac{1}{2}+\frac{1}{4}\right) \right) \\ \\ ∪&\displaystyle\left[ b\left(\frac{1}{2}+\frac{1}{4} \right),b\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\right) \right) \\ \\ ∪&\vdots \end{array}
例えば「空集合( b=a+ε )」を利用して
このように定義することで
\begin{array}{llllll} \displaystyle \left[ a,b\sum_{n=1}^{k}\frac{1}{2^n} \right)&\overset{k\to\infty}{\to}&[a,b) \end{array}
「任意の区間 [a,b) 」を
「非交和 \mathrm{disjoint} 」の条件下において
「無限和で作ることが可能」なので
\begin{array}{llllllll} \displaystyle μ\Bigl( [a,b) \Bigr) &=&\displaystyle μ\left( \left[a,b\frac{1}{2} \right) \right)+\sum_{n=1}^{\infty} μ \left( \left[ b\sum_{k=1}^{n}\frac{1}{2^k}, b\sum_{k=1}^{n+1}\frac{1}{2^k} \right) \right) \\ \\ \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) &=&\displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
「区間の長さ μ 」の対応範囲である
「全ての区間 [a,b) 」で
「完全加法性」の条件が満たされることから
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &&→&& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) &=&\displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
「区間の長さ μ 」は
「完全加法的集合関数」であると言えます。
(測度以外の完全加法性は無限和集合に制限がある)
区間塊の長さは完全加法的集合関数である
以上の話を元に
「区間塊の長さ μ^+ 」について考えていきます。
\begin{array}{ccccccc} \mathrm{disjoint} &&→&&F&=&\displaystyle\bigcup_{n=1}^{k}I_n \\ \\ \mathrm{disjoint} &&→&& μ^+\left( F \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
「区間塊 F 」と
「区間塊の長さ μ^+ 」の定義はこれで
\begin{array}{llllll} \mathrm{disjoint} &&→&& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty}F_n \right) &=& \displaystyle \sum_{n=1}^{\infty}μ^+(F_n) \end{array}
着地はここ
区間塊の長さは有限加法的である
とりあえずこれから考えていくと
\begin{array}{llllll} \displaystyle F_1&=&\displaystyle \bigcup_{n=1}^{k_1}I_n &&&&μ^+\left( F_1 \right)&=&\displaystyle \sum_{n=1}^{k_1}μ(I_n) \\ \\ \displaystyle F_2&=&\displaystyle \bigcup_{n=k_1+1}^{k_1+k_2}I_n &&&&μ^+\left( F_2 \right)&=&\displaystyle \sum_{n=k_1+1}^{k_1+k_2}μ(I_n) \end{array}
\begin{array}{llllll} \displaystyle F_1∪F_2&=&\displaystyle \bigcup_{n=1}^{k_1+k_2}I_n \end{array}
これは前提に「非交和」の条件がくる以上
\begin{array}{ccccccc} \mathrm{disjoint} &&→&&F&=&\displaystyle\bigcup_{n=1}^{k}I_n \\ \\ \mathrm{disjoint} &&→&& μ^+\left( F \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
「区間」も「非交和」ですから
\begin{array}{llllll} \displaystyle μ^+\left( F_1∪F_2 \right)&=&\displaystyle \sum_{n=1}^{k_1+k_2}μ(I_n) \\ \\ &=&\displaystyle \sum_{n=1}^{k_1}μ(I_n)+\sum_{n=k_1+1}^{k_1+k_2}μ(I_n) \\ \\ &=&\displaystyle μ^+\left(F_1 \right)+μ^+\left( F_2 \right) \end{array}
定義を辿れば導けるので
\begin{array}{llllll} \mathrm{disjoint} &&→&& μ^+\left( F_1∪F_2 \right)&=&\displaystyle μ^+\left(F_1 \right)+μ^+\left( F_2 \right) \\ \\ \mathrm{disjoint} &&→&& \displaystyle μ^+\left( \bigcup_{n=1}^{k}F_n \right) &=& \displaystyle \sum_{n=1}^{k}μ^+(F_n) \end{array}
特に疑問も無く
この結論はすぐに導けます。
非交和な区間塊の和集合
「区間塊」の定義を考えると
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& (I_1∪I_2)∪(I_3∪I_4)=I_1∪I_2∪I_3∪I_4 \end{array}
「区間塊」は
「非交和な区間の和集合」ですから
\begin{array}{llllll} \displaystyle F_1∪F_2&=&\displaystyle \left( \bigcup_{n_1=1}^{k_1}I_{n_1} \right)∪\left( \bigcup_{n_2=1}^{k_2}I_{n_2} \right) \end{array}
「共通部分が無い」以上
和集合をとれば
\begin{array}{llllll} \displaystyle F_1∪F_2&=&\displaystyle \left( \bigcup_{n_1=1}^{k_1}I_{n_1} \right)∪\left( \bigcup_{n_2=1}^{k_2}I_{n_2} \right) \\ \\ &=&\displaystyle \left( \bigcup_{n=1}^{k_1}I_{n} \right)∪\left( \bigcup_{n=k_1+1}^{k_1+k_2}I_{n} \right) \\ \\ &=&\displaystyle\bigcup_{n=1}^{k_1+k_2}I_{n} \end{array}
添え字を変えるだけで
そのまま「非交和な区間の和集合」になり
「1つの区間塊」になるので
この手順で「1つの区間塊」にした後
また他の「非交和な区間塊」と和集合をとれば
\begin{array}{llllll} \displaystyle (F_1∪F_2)∪F_3&=&\displaystyle\bigcup_{n=1}^{k_1+k_2+k_3}I_{n} \end{array}
同様の結果を繰り返すことになるため
必然、以下の「非交和な区間塊の和集合」は
\begin{array}{llllll} \displaystyle\bigcup_{n=1}^{k}F_{n}&=& \displaystyle\bigcup_{n=1}^{u}I_{n} \end{array}
「1つの区間塊」になると言えます。
(集合環であるため明らかとしても良い)
非交和な区間塊の和集合と無限和
「区間塊」は「区間」でもある以上
「無限和」の存在は明らかです。
\begin{array}{llllll} \displaystyle μ^+\Bigl( [a,b) \Bigr)&=&μ\Bigl( [a,b) \Bigr) \\ \\ &=&b-a \end{array}
「区間塊の長さ μ^+ 」で測れる
「無限和(この時点では区間)」は確実に存在し
\begin{array}{ccccccc} \mathrm{disjoint} &&→&&F&=&\displaystyle\bigcup_{n=1}^{k}I_n \\ \\ \mathrm{disjoint} &&→&& μ^+\left( F \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
またそれと同様に
「区間塊の長さ μ^+ 」の定義から
\begin{array}{llllll} \displaystyle μ^+\Bigl( [a,b)∪[c,d) \Bigr) &=&\displaystyle μ\Bigl( [a,b) \Bigr) +μ\Bigl( [c,d) \Bigr) \\ \\ &=&(b-a)+(d-c) \end{array}
このような「区間塊」の長さもまた
確実に求めることができます。
区間塊の無限和と区間
以上の結果から
「区間塊の長さ μ^+ 」の定義より
\begin{array}{ccccccc} \mathrm{disjoint} &&→&&F&=&\displaystyle\bigcup_{n=1}^{k}I_n \\ \\ \mathrm{disjoint} &&→&& μ^+\left( F \right)&=&\displaystyle \sum_{n=1}^{k}μ(I_n) \end{array}
「区間塊の和集合」が
「区間塊」になること
\begin{array}{llllll} F_1,F_2∈\mathrm{Figure} &&→&& \displaystyle F_1∪F_2∈\mathrm{Figure} \end{array}
「区間塊の和集合」が
「1つの区間塊」になることから
\begin{array}{llllll} \displaystyle (F_1∪F_2)∪F_3&=&\displaystyle\bigcup_{n=1}^{k_1+k_2+k_3}I_{n} \end{array}
「区間塊の無限和」は
「区間塊」になるとは限りませんが
「 μ^+ で測れる区間塊の無限和」は
確実に「区間塊」でなければならないため
\begin{array}{llllll} \displaystyle μ^+\left( \bigcup_{n=1}^{\infty}F_n \right) &\in& R_+ \\ \\ && R_+=\{ x∈R \mid 0≤x<\infty \} \end{array}
これは必ず正の実数になり
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}F_n &=& \displaystyle F_1∪ F_2 ∪ F_3 \cdots \\ \\ &=& \displaystyle \left( \bigcup_{n=1}^{k_1}I_{n} \right) ∪\left( \bigcup_{n=k_1+1}^{k_1+k_2}I_{n} \right)∪\left( \bigcup_{n=k_1+k_2+1}^{k_1+k_2+k_3}I_{n} \right)∪\cdots \end{array}
この「区間塊にならなければならない無限和」は
当然「区間塊」ですから
\begin{array}{llllll} F_n &=& \displaystyle \bigcup_{i=1}^{k_n}I_{ni} \end{array}
「区間塊 F_n 」が
「 k_n 個の非交和な区間」の和集合だとすると
\begin{array}{rcc} \displaystyle \sum_{n=1}^{m}k_n&=&u \\ \\ \displaystyle \lim_{m\to\infty} \sum_{n=1}^{m}k_n&=&\infty \end{array}
その「区間塊の和集合」の
「区間の個数 u 」はこうなり
\begin{array}{rcr} F_n &=& \displaystyle \bigcup_{i=1}^{k_n}I_{ni} \\ \\ \displaystyle \bigcup_{n=1}^{\infty}F_n &=&\displaystyle\bigcup_{n=1}^{\infty}\bigcup_{i=1}^{k_n}I_{ni} \end{array}
結果、こうなります。
無限和集合の定義
↑ は「無限和集合」の定義を省略した話なので
念のため、きちんと定義を確認しておきます。
\begin{array}{lcr}\displaystyle x\in \bigcup_{i=1}^{k_n}I_{ni} &⇔& x\in F_n \\ \\ \displaystyle x\in \bigcup_{n=1}^{\infty}F_n &⇔& \exists n\in N \,\,x\in F_n \end{array}
使うのはこの2つ
これを見て分かると思いますが
\begin{array}{rcr} \exists n\in N \,\,x\in F_n &⇔&\displaystyle \exists n\in N \,\,x\in \bigcup_{i=1}^{k_n}I_{ni} \\ \\ x\in \displaystyle \bigcup_{n=1}^{\infty}F_n &⇔& x\in \displaystyle\bigcup_{n=1}^{\infty}\bigcup_{i=1}^{k_n}I_{ni} \end{array}
特に難しい操作は無く
この関係はすぐに導かれます。
記述の省略
↑ で出てくる ↓ についてですが
\displaystyle\bigcup_{n=1}^{\infty}\bigcup_{i=1}^{k_n}I_{ni}
これは要は「区間の集まり」ですから
\begin{array}{ccc} \displaystyle\bigcup_{n=1}^{\infty}\bigcup_{i=1}^{k_n}I_{ni}&=&\displaystyle\bigcup_{n=1}^{\infty}I_{n} \end{array}
記述を簡単にするために
ここでこのように書き換えておきます。
(添え字に使う文字はなんでもいい)
当然ですが
「どの F_n を構成するか」というような
そういう意味は確かに薄れます。
\begin{array}{lcl} 11 &→& 1 \\ \\ 12 &→& 2 \\ \\ & \vdots \\ \\ 1k_1 &→& k_1 \\ \\ 21 &→& k_1+1 \\ \\ &\vdots \\ \\ 2k_2 &→& k_1+k_2 \\ \\ & \vdots \\ \\ ni &→& \displaystyle\sum_{m=1}^{n-1}k_{m}+i \\ \\ &\vdots \end{array}
しかし添え字を減らしても
\begin{array}{lcl} 0<i≤k_1 &→& F_1 \\ \\ k_1<i≤k_1+k_2 &→& F_2 \\ \\ &\vdots \\ \\ \displaystyle \sum_{m=1}^{n-1}k_m <i≤ \sum_{m=1}^{n}k_m &→& F_n \\ \\ &\vdots \end{array}
このようにすれば所在は特定できるため
\begin{array}{ccc} \displaystyle\bigcup_{i=1}^{\infty}I_{i}&&\displaystyle\bigcup_{n=1}^{\infty}I_{n} \end{array}
仮にこのようにしたとしても
特に問題は発生しません。
区間塊の長さの無限和と区間の長さ
「非交和」は前提として
「区間塊の無限和」が「区間塊」になる場合
\begin{array}{ccc} \displaystyle \bigcup_{n=1}^{\infty}F_n &=&\displaystyle \bigcup_{n=1}^{\infty}I_n \\ \\ \displaystyle μ^+\left( \bigcup_{n=1}^{\infty}F_n \right) &=&\displaystyle μ^+\left( \bigcup_{n=1}^{\infty}I_n \right) \end{array}
こうなることは分かりましたが
\begin{array}{ccl} \displaystyle \sum_{n=1}^{\infty}μ^+(F_n) &=&μ^+(F_1)+μ^+(F_2)+μ^+(F_3)+\cdots \end{array}
\displaystyle \sum_{n=1}^{\infty}μ^+(F_n)
この部分がどうなるのかについては
まだよく分かっていません。
とはいえ
これについても
定義通りに話を進めていけば
\begin{array}{llllll} \displaystyle \sum_{n=1}^{\infty}μ^+(F_n)&=& \displaystyle μ^+(F_1)+μ^+(F_2)+μ^+(F_3)+\cdots \\ \\ &=&\displaystyle \sum_{n=1}^{k_1}μ(I_n) + \sum_{n=k_1+1}^{k_1+k_2}μ(I_n)+\sum_{n=k_1+k_2+1}^{k_1+k_2+k_3}μ(I_n)+\cdots \\ \\ &=& \displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
「区間の長さ μ 」の「完全加法性」より
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &→& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right)= \sum_{n=1}^{\infty}μ(I_n) \end{array}
\begin{array}{llllll} \displaystyle \sum_{n=1}^{\infty}μ^+(F_n)&=& \displaystyle\sum_{n=1}^{\infty}μ(I_n) \\ \\ &=&\displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) \end{array}
この関係が得られるので
これで
「区間塊の無限和」についての
\begin{array}{ccc} \displaystyle \sum_{n=1}^{\infty}μ^+(F_n)&=& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) \end{array}
良い感じになりそうな関係は得ることができます。
区間塊の長さは完全加法的集合関数である
以上のことから
\begin{array}{llllll} \displaystyle \mathrm{disjoint} &&→&& \displaystyle μ\left( \bigcup_{n=1}^{\infty} I_n \right) &=&\displaystyle \sum_{n=1}^{\infty}μ(I_n) \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}F_n && && &=&\displaystyle \bigcup_{n=1}^{\infty}I_n \\ \\ \displaystyle \sum_{n=1}^{\infty}μ^+(F_n)&=&\displaystyle \sum_{n=1}^{\infty}μ^+(I_n)&=&\displaystyle \sum_{n=1}^{\infty}μ(I_n)&=&\displaystyle μ\left( \bigcup_{n=1}^{\infty}I_n \right) \end{array}
「区間塊」の範囲で
\begin{array}{llllll} \mathrm{disjoint} &&→&& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty}F_n \right) &=& \displaystyle μ\left( \bigcup_{n=1}^{\infty}I_n \right) \\ \\ \mathrm{disjoint} &&→&& \displaystyle μ^+\left( \bigcup_{n=1}^{\infty}F_n \right) &=& \displaystyle \sum_{n=1}^{\infty}μ^+(F_n) \end{array}
この関係が成立すると言えるので
「区間塊の長さ μ^+ 」は
「完全加法的集合関数」であると言えます。
