|| 曲がってる図形を調べる方法
「曲線」での『傾き(微分)』と『面積(積分)』の話。
スポンサーリンク
目次
微分「曲線での点の傾きを求める方法」
積分「曲線の面積を求める方法」
数学で難しいとされる知識の代表格
それが「微分」と「積分」なわけですが
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h)-x} \\ \\ S&=&\displaystyle \int_{a}^{b}f(x)\,dx \end{array}
実はこれ、そんな難しい話ではありません。
\begin{array}{llllll} \displaystyle /&& y&=&ax &&a \\ \\ □ && S&=&a\times b &&S \end{array}
というのも、これらがやっていることは単純で
「微分」は『傾き a 』を求めているだけ
「積分」は『長方形の面積 S 』を求めてるだけなんですよ。
まあつまり小中学で習った
「長方形の面積」「傾き」が分かるなら
\begin{array}{llllll} \displaystyle \lim_{x\to a}x&=&a \end{array}
後は「極限」の『近付ける』
という感覚さえ理解できていれば
微分と積分は簡単に理解できます。
ただまあそれ以前の話
複雑な計算処理は機械的に処理される現代では
これは感覚を理解してさえていれば十分で
式の意味を理解できるレベルにあるなら
それだけで困ることはない知識と言えます。
なので感覚だけ覚えてればOKで
なにやら複雑な記号を覚える必要はありません。
微分 Derivative
|| 曲線の点の傾きを求めるやり方
関数の「ある一点」の『変化量』を求める方法。
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h)-x} \\ \\ \\ a&=&\displaystyle \frac{(a(x+k)+b)-(ax+b)}{(x+k)-x} \end{array}
この性質上、必然的に『接線』が導かれます。
\begin{array}{llllll} \displaystyle y-f(a)&=&f^{\prime}(a)(x-a) \end{array}
これは『曲線』を考えるための考え方ですが
やってることは「直線」の操作と同様です。
特別な操作は行われていません。
補足しておくと
この操作は ↓ のような省略形で書かれることが多いです。
\begin{array}{llllll} \displaystyle dx&=&\displaystyle\lim_{h\to 0}\Bigl( (x+h)-x \Bigr) \\ \\ df(x)&=&\displaystyle\lim_{h\to 0}\Bigl( f(x+h)-f(x) \Bigr) \end{array}
\begin{array}{llllll} f^{\prime}(x) &=&\displaystyle \frac{df(x)}{dx}\\ \\ &=&\displaystyle \frac{dy}{dx} \end{array}
「記号 d 」は『微小・差』を表す記号ですが
これ自体にはそんな意味は無いので
\begin{array}{llllll} \displaystyle Δx&=&\displaystyle\lim_{h\to 0}\Bigl( (x+h)-x \Bigr) \\ \\ Δf(x)&=&\displaystyle\lim_{h\to 0}\Bigl( f(x+h)-f(x) \Bigr) \\ \\ \\ \displaystyle \partial x&=&\displaystyle\lim_{h\to 0}\Bigl( (x+h)-x \Bigr) \\ \\ \partial f(x)&=&\displaystyle\lim_{h\to 0}\Bigl( f(x+h)-f(x) \Bigr) \end{array}
このように他の記号で書いても問題はありません。
曲がってる図形
『曲線・曲面』を考える時
「傾き」や「面積」なんかを求めるとなると
\begin{array}{llllll} \displaystyle f(x)&=&x^2 \end{array}
『そのまま』では
私たち人間にはうまい方法が浮かびません。
\begin{array}{llllll} \displaystyle a&=&\displaystyle \frac{(a(x+k)+b)-(ax+b)}{(x+k)-x} \\ \\ 1&=&\displaystyle \frac{((x+1)+2)-(x+1)}{(x+2)-x} \end{array}
私たち人間ができるのは
あくまで「直線」「長方形」の性質を求めることのみで
つまり『曲線』のあれこれを調べるとなると
その「曲線」に似せるために
たくさんの「直線」を細切れにして繋げてみたり
曲線に近い「面積が分かる図形」を用意したり
とまあそういった感じで
『近似』して求めるしかありません。
微分の発想
微分は『曲線の傾き』を
「直線を使って求める」やり方で
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h)-x} \end{array}
h\to 0 は「めっちゃ近くで見る」
ということを意味する感じで
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\Bigl( f(x+h)-f(x) \Big)&=&0 \end{array}
これは「曲線」が『ほぼ直線』だと言える
みたいなことを意味する部分になります。
まあ要は「すごい近づいて見る」と
「曲がり方」は『緩やかになる』
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\Bigl( f(x+h)-f(x) \Big)&=&0 \\ \\ \displaystyle \lim_{h\to 0}\Bigl( (x+h)-x \Big)&=&0 \end{array}
つまり『曲線』は「直線に近似できる」って話で
これによって曲線の傾きを求めている、と。
まあざっくり言うと
微分はこんな感じの発想から生まれた手法になります。
積分 Integral
|| 曲面の面積を求めるやつ
『長方形の 縦 × 横』を使って曲面の面積を求める方法。
\begin{array}{llllll} \displaystyle S&=&\displaystyle \int_{a}^{b}f(x)\,dx \end{array}
「長方形の面積」を求める部分は ↓
\begin{array}{llllll} \displaystyle f(x)\times dx \end{array}
求めた『細長い長方形の面積』
この「総和 S 」を意味するのが ↓ の記号になります。
\begin{array}{llllll} \displaystyle \sum&≒&\displaystyle\int \end{array}
『 dx は底辺』『 f(x) は高さ』
こうするとイメージしやすいかもしれません。
発想
この操作は「めっちゃ細い長方形」に区切って
その「全てを集めれば良い」って感じで
\begin{array}{llllll} \displaystyle \displaystyle \int_{a}^{b}f(x)\,dx \end{array}
『 f(x)\,dx の集まり』が求める「面積」だ、みたいな。
まあつまりは「厚みのある線の面積の合計」から
「複雑な図形の面積」を得られるんじゃね?
みたいな感じで
\begin{array}{llllll} \displaystyle dx&=&\displaystyle\lim_{h\to 0}\Bigl( (x+h)-x \Bigr) \end{array}
実際、これの「 h 」を『 0 に近づければ』
『ほとんど直線に見える長方形』が得られますから
\begin{array}{llllll} \displaystyle f(x)dx+f(x+dx)dx+f(x+dx+dx)dx\cdots \end{array}
結果的に面積が求まる、と。
まあそういう感じです。
微分と積分の関係
微分の操作は「傾きを求める」という点で明確なため
特に疑問らしい疑問は出てきません。
\begin{array}{llllll} \displaystyle f^{\prime}(x)&=&\displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h)-x} \end{array}
しかし「積分」の操作に関しては
実際にはどのような操作を行っているのか
\begin{array}{llllll} S&=&\displaystyle \int_{a}^{b}f(x)\,dx \end{array}
なんだかよく分からない、とは思いませんか?
\begin{array}{llllll} \displaystyle f(a)dx+f(a+dx)dx+f(a+2dx)dx+\cdots +f(b-dx)dx \end{array}
実際、一般形に置き換えてみるとなんか微妙な感じで
実際にはどのような操作を行えばいいのか
その辺りがはっきりしません。
分かる操作を使ってみる
微分と積分が逆操作である。
\begin{array}{llllll} \displaystyle \int f(x)\,dx&=&F(x)+C \\ \\ f(x)&=&\displaystyle \frac{dF(x)}{dx} \end{array}
理由は知らないにしても
この事実を知ってる人は多いと思います。
\begin{array}{llllll} \displaystyle f(x)&=&\displaystyle \frac{dF(x)}{dx} \end{array}
ただこれ、実は結果論でして
重要なのはこの関係の方だったりします。
\begin{array}{llllll} \displaystyle f(x)\,dx \end{array}
というのも積分の具体的な操作を見るに
求めたいのはこの部分です。
\begin{array}{llllll} \displaystyle f(x)\,dx&=&?\end{array}
つまりこれを
どうにか「具体的な形」にしなければならないわけで
\begin{array}{llllll} \displaystyle \frac{dF(x)}{dx} &=&f(x) \\ \\ \displaystyle dF(x) &=&f(x)\,dx \end{array}
その試みの1つとして
このような「関数 F(x) 」が考えられた。
これが重要で
この試みが実を結んだ結果が
『微分と積分は逆操作である』になります。
実際に計算してみる
定積分を考えてみます。
\begin{array}{llllll} \displaystyle \int_{0}^{a}f(x)\,dx \end{array}
とりあえず分かりやすいように
範囲は 0≤x≤a でとってみましょうか。
\begin{array}{llllll} \displaystyle \frac{dF(x)}{dx} &=&f(x) \\ \\ \displaystyle dF(x) &=&f(x)\,dx \end{array}
その上でこのような関数 F を考えてみます。
(この F は原始関数と呼ばれることがあります)
\begin{array}{llllll} \displaystyle dF(x)&=&\displaystyle\lim_{h\to 0} F(x+h)-F(x) \\ \\ dx&=&\displaystyle\lim_{h\to 0}(x+h)-x \end{array}
確認しておくとこうで
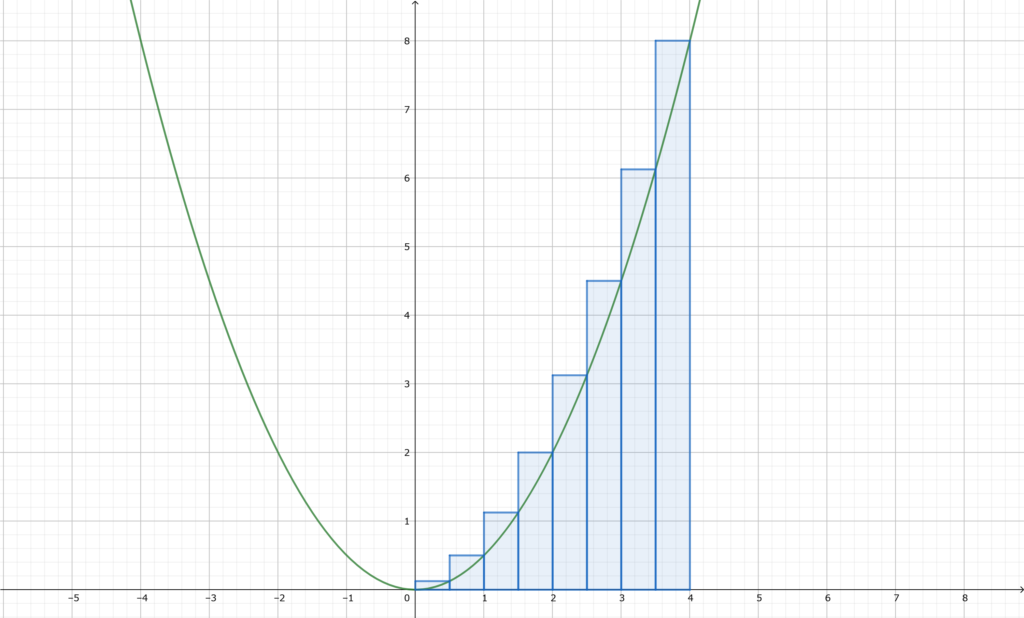
\begin{array}{llllll} \displaystyle \int_{0}^{a}f(x)\,dx&=&f(dx)dx+f(2dx)dx+\cdots+f(a-dx)dx+f(a)dx \end{array}
積分で求められる面積は
今回は図のように求めてるので
「左端の点 f(0) 」を除けばこうなりますから
\begin{array}{llllll} \displaystyle \int_{0}^{a}f(x)\,dx&=&f(dx)dx+f(2dx)dx+\cdots+f(a-dx)dx+f(a)dx \\ \\ &=&dF(dx)+dF(2dx)+\cdots+dF(a-dx)+dF(a) \end{array}
よく分からない部分 f(x)\,dx を置き換えると
\begin{array}{llllll} \displaystyle \displaystyle \int_{0}^{a}f(x)\,dx&=&dF(dx)+dF(2dx)+\cdots+dF(a-dx)+dF(a) \\ \\ \\ &=&\displaystyle\lim_{h\to 0}\Bigl(\textcolor{skyblue}{F(h+h)}-F(h) \Bigr)+\Bigl(\textcolor{gray}{F(2h+h)}\textcolor{skyblue}{-F(2h)} \Bigr)+\cdots \\ \\ &&\cdots+\Bigl(\textcolor{pink}{F(a-h+h)}\textcolor{silver}{-F(a-h)} \Bigr)+\Bigl( F(a+h)\textcolor{pink}{-F(a)} \Bigr) \\ \\ \\ &=&\displaystyle\lim_{h\to 0} -F(h)+F(a+h) \\ \\ &=&F(a)-F(0) \end{array}
左右で打ち消し合って
打ち消す相手のいない2つだけが残って
なんかうまいことこうなります。
そして以下の項目は明確ですから
\begin{array}{llllll} \displaystyle f(x) \\ \\ \displaystyle \frac{dF(x)}{dx} &=&f(x) \\ \\ \displaystyle \int_{s}^{a}f(x)\,dx&=&F(a)-F(s) \end{array}
これで「明確な手順」で
積分値が求められるようになります。
