|| 微分の単位的な数学の基本定数
自然対数の底とか言われてるやつで
微分で多く使われる概念になります。
スポンサーリンク
数式での表現は
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n&=&e \end{array}
\begin{array}{llllll} \displaystyle \frac{d}{dx}e^x&=&e^x \end{array}
定義はこんな感じで
\begin{array}{llllll} \displaystyle e&=&\displaystyle 1+\frac{1}{1!}+\frac{1}{2!} +\frac{1}{3!}+\cdots \end{array}
具体的な値はこんな感じです。
目次
自然対数の底「ネイピア数の厳密な定義」
指数関数「指数に変数が来るやつ」
対数関数「指数を求めるやつ」
対数関数の微分「定義の基礎」
ネイピア数の発見「連続複利と指数関数の微分」
連続複利「ネイピア数が出てくる計算」
指数関数の微分「微分してもそんな変化しない」
ネイピア数の導出「具体的に出す」
マクローリン展開「関数の多項式展開」
定数の一致「自然対数の底と変化しない微分」
指数関数 Exponential
|| 変数 x が指数に来る関数
冪乗を考えると出てくる関数のこと
\begin{array}{llllll} \displaystyle y&=&a^x \end{array}
こういうやつです。
対数関数 Logarithm
|| 指数を求める関数
指数関数の「逆関数」のこと
\begin{array}{rllllll} \displaystyle y&=&a^{x} \\ \\ \log_a y&=&x \end{array}
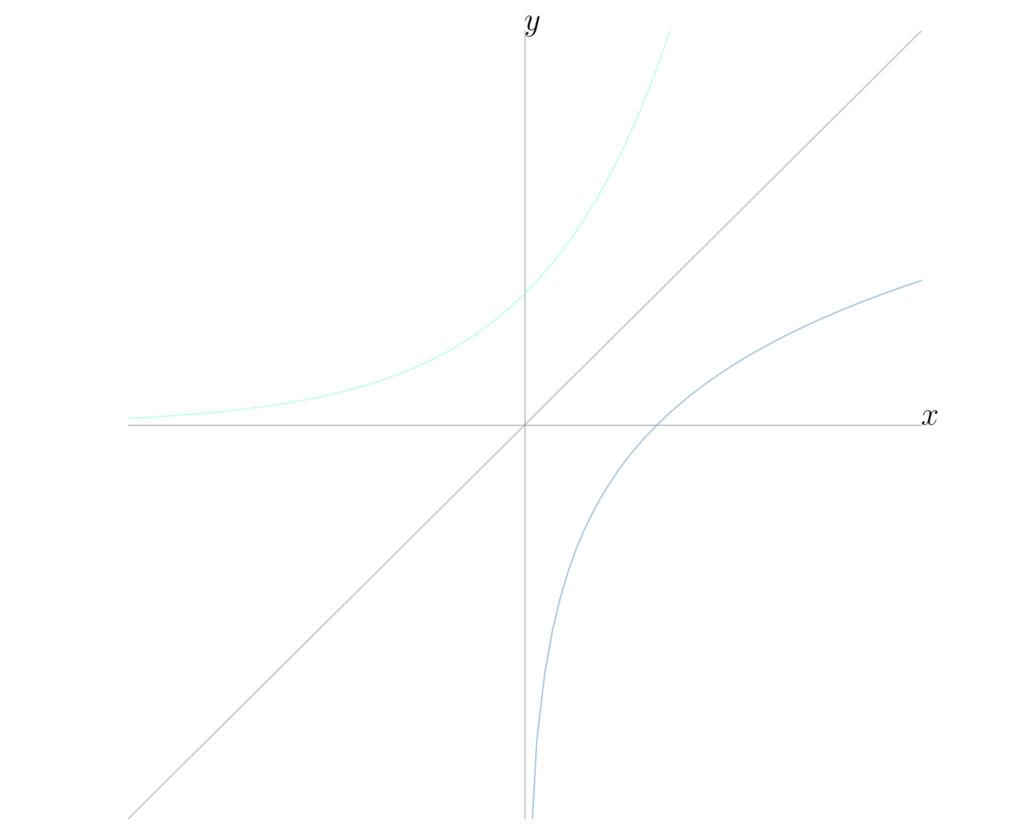
「指数」を求めていて
この時の a を「底」と言います。
\begin{array}{llllll} \displaystyle a&=&\displaystyle a^{\log_a a} \\ \\ a^1&=&\displaystyle a^{\log_a a} \\ \\ 1&=&\log_a a \\ \\ \\ \displaystyle a^0&=&\displaystyle a^{\log_a a^0} \\ \\ a^0&=&\displaystyle a^{\log_a 1} \\ \\ 0&=&\log_a 1 \end{array}
具体的にはこんな感じになって
\begin{array}{cllllll} 2\times3&=&6 \\ \\ \displaystyle a^{\log_a 2}\times a^{\log_a 3} &=&a^{\log_a 6} \\ \\ \\ a^{\log_a 2+\log_a 3} &=&a^{\log_a 6} \\ \\ \log_a x +\log_a y &=&\log_a xy \end{array}
例えばこういう操作ができます。
\begin{array}{llllll} \displaystyle 2^3 &=& a^{\log_a 2^3 } \\ \\ 2^3 &=& \displaystyle\left(a^{ \log_a 2 } \right)^{3} \\ \\ &=&a^{ 3\log_a 2 } \end{array}
\begin{array}{llllll} \displaystyle \log_a b^x&=&x\log_a b \end{array}
他にこういうのもよく使いますね。
\begin{array}{llllll} \displaystyle \log_a b&=&\displaystyle \frac{\log_c b}{\log_c a} \end{array}
\begin{array}{rcrlllll} \displaystyle a^{\log_a b }&=&b \\ \\ \log_c a^{\log_a b }&=&\log_c b \\ \\ \log_a b\log_c a&=&\log_c b \end{array}
こういう「底の変換」もたまに使います。
自然対数 Natural Logarithm
|| 逆関数と傾きの感覚
「対数関数」の最も単純な形
\begin{array}{rllllll} \displaystyle \log_e x&=&y \\ \\ x&=&e^y \end{array}
\begin{array}{llllll} \displaystyle \log_e x &=&\log x \\ \\ &=&\ln x \end{array}
記号だとこんな感じ。
ネイピア数の厳密な定義
「対数関数の微分」を使うと
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n&=&e \end{array}
こいつが「収束する」のは確かであることから
(詳しくは後述)
\begin{array}{llllll} \displaystyle \frac{d}{dx} \log_c x&=&\displaystyle \lim_{t\to\infty} \left(\log_c \left( 1+\frac{1}{t} \right)^t \right) \frac{1}{x} \end{array}
\begin{array}{rccllllll} \displaystyle \frac{d}{dx} \log_c x&=&\displaystyle\left(\log_c e\right)\frac{1}{x} \\ \\ \log_c e&=&\displaystyle \int_{1}^{e} \left(\log_c e\right)\frac{1}{x} \,dx \\ \\ &=&\log_c e - \log_c 1 \end{array}
\begin{array}{llcllll} \displaystyle \log_c e&=&? \\ \\ \log_e e&=&1 \end{array}
「対数の底」を収束値 e とすれば
\begin{array}{rcrllllll} \displaystyle \frac{d}{dx} \log_e x&=&\displaystyle\left(\log_e e\right)\frac{1}{x} \\ \\ \displaystyle \frac{d}{dx} \log_e x&=&\displaystyle \frac{1}{x} \\ \\ \\ \log_e a&=&\displaystyle \int_{1}^{a} \left(\log_e e\right)\frac{1}{x} \,dx \\ \\ &=&\displaystyle \int_{1}^{a} \frac{1}{x} \,dx \end{array}
「自然対数」で考えると
このように綺麗な形に整理することができるため
\begin{array}{rccllllll} \displaystyle \log_e a&=&1 \\ \\ a&=&e \end{array}
「ネイピア数」はこの条件を満たす
「自然対数の底 e 」として定義されています。
いやちょっと複雑じゃない?ってなるかもですが
実は厳密さを担保できるのは
この定義だけだったりします。
変な定数の発見
「ネイピア数」の話は少し込み入ってます。
\begin{array}{cllllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n &=&e \\ \\ \displaystyle \lim_{h\to 0}\frac{e^h-1}{h}&=&1 \end{array}
というのも
これは複数のやり方で求められてるんですが
それらが「一致するか」はその時点では不明
つまり一致したのは「結果論」で
そのせいで話が少しとっ散らかっている。
とまあそんな感じなので
ちょっと大変。
連続複利 Continuous Compound
|| ネイピア数が最初に出てきた計算
複利計算からよく分からん定数が出てくる
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n &=&? \end{array}
この話は別で代替できないのか。
そう考える人は一定数いると思いますが
実は「ネイピア数」を考える上で
この話は避けて通れなかったりします。
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n \end{array}
というのも
この形の式が有限の値に『収束』する
これが保証されなければ
「対数関数の微分」はそもそも定義できないので。
複利の概要
本筋から逸れるので軽く紹介
↑ の計算式が出てくる経緯と用語をざっくりと。
\begin{array}{llllll} \displaystyle p+pi&=&p(1+i) \end{array}
まずこの式は以下を意味するものです。
「元金 \mathrm{Principal} 」(貸した金・投資した金)
「利子 \mathrm{Interest} 」(リターン・貸す利益)から
\begin{array}{llllll} \displaystyle p(1+i) \\ \\ p(1+0.01) \end{array}
式全体は「元利合計」を
p はそのまま「元金」を
i は「年利」なんかの「利率」を表すとします。
ここで
例えば「年利 i 」とし
「 n 年間」銀行に貸していたとすると
\begin{array}{llllll} \displaystyle p_0&=&p_0 \\ \\ p_1&=&p_0+p_0i \\ \\ &=&p_0(1+i) \end{array}
「元利合計」の
1 年目はこんな感じで
\begin{array}{llllll} \displaystyle p_2 &=&p_0+p_0(2i) \end{array}
2 年目の「単利計算」だとこう
\begin{array}{llllll} \displaystyle p_2 &=&p_1+p_1i \\ \\ &=&p_0+p_0i+(p_0+p_0i)i \\ \\ &=&p_0(1+i)+p_0(1+i)i \\ \\ &=&(1+i)p_0(1+i) \\ \\ &=&p_0(1+i)^2 \end{array}
2 年目の「複利計算」だとこうなります。
\begin{array}{lcllll} \displaystyle p_{n+1}&=&p_n+p_ni \\ \\ &=&p_n(1+i) \\ \\ \\ &=&p_{n-1}(1+i)^2 \\ \\ &\vdots \\ \\ &=&p_0(1+i)^{n+1} \end{array}
でまあ計算してみると
n+1 年目の「複利計算」は当然こうなります。
複利計算と変な式
ここから更に
「期間」と「利率」を共にいじって
\begin{array}{llllll} \displaystyle 1 \, \mathrm{year}&=&2\, \mathrm{half}\text{-}\mathrm{year} \end{array}
\begin{array}{llllll} \displaystyle p_0(1+i)^{n}&&\to&& \displaystyle p_0\left(1+\frac{i}{2} \right)^{2k} \end{array}
例えば
「半年」で利息がつくなら「利率は半分」
とするならこうなって
\begin{array}{llllll} \displaystyle 1 \, \mathrm{year}&=&2\, \mathrm{half}\text{-}\mathrm{year} \\ \\ &=&12 \,\mathrm{month} \\ \\ &=&12\times 7 \,\mathrm{week} \\ \\ &=&365 \, \mathrm{day} \end{array}
これはいくらでも分割できますから
\begin{array}{llllll} \displaystyle p_0\left(1+\frac{i}{j} \right)^{jk} \end{array}
このように書ける。
\begin{array}{cccllllll} \displaystyle \frac{i}{j} &=&\displaystyle \frac{1}{t} \\ \\ j&=&it \end{array}
\begin{array}{llllll} \displaystyle \left(1+\frac{i}{j} \right)^{jk} \\ \\ \displaystyle \left(1+\frac{1}{t} \right)^{itk} &=&\displaystyle \left(1+\frac{1}{t} \right)^{t(ik)} \\ \\ &=&\displaystyle \left( \left(1+\frac{1}{t} \right)^{t} \right)^{ik} \end{array}
結果、この式から
「ネイピア数になるもの」が導ける。
\begin{array}{llllll} \displaystyle \left(1+\frac{1}{t} \right)^{t} \end{array}
この一連の流れとこの複利計算の式が
この話が重要になる理由になります。
変なやつは収束する?
ネイピア数の厳密な定義の核
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n \end{array}
それは
これが「収束する」ことで
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n &<&? \end{array}
これを証明しないことには
ネイピア数を厳密には取り扱えません。
比較できる形に式変形
こいつの性質を考えてみると
\begin{array}{cllllll} \displaystyle \left(1+ \frac{1}{n} \right)^n \\ \\ \displaystyle (1+α)^n \end{array}
「 1 以上の冪乗」ですから
まあほぼほぼ間違いなく単調増加
\begin{array}{ccllllll} \displaystyle a_{n}&<&a_{n+1} \\ \\ 0&<&a_{n+1}-a_n \end{array}
感覚的には特に疑いの余地はありませんが
厳密に確認しないとどうにもスッキリしない。
\begin{array}{lllllll} a_n&=&\displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n \\ \\ &=&\displaystyle \lim_{n\to \infty} \left(\frac{n+1}{n} \right)^n \\ \\ \\ a_{n+1} &=&\displaystyle \lim_{n\to \infty} \left( 1+\frac{1}{n+1} \right)^{n+1} \\ \\ &=&\displaystyle \lim_{n\to \infty} \left( \frac{n+1+1}{n+1} \right)^{n+1} \end{array}
というわけで示したいんですが
まあこんな感じでよく分からない
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n &=& \displaystyle \sum_{k=0}^{n} {}_n \mathrm{C}_{k}1^{n-k} \left(\frac{1}{n}\right)^k \\ \\ &=& \displaystyle \sum_{k=0}^{n} {}_n \mathrm{C}_{k} \frac{1}{n^k} \\ \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{n!}{k!(n-k)!} \times \frac{1}{n^k} \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \frac{n!}{(n-k)!}\times \frac{1}{n^k} \end{array}
なので比較しやすい形にするために
「二項定理」で式を分解してみると
\begin{array}{llllll} \displaystyle \frac{n!}{(n-k)!} &=&\displaystyle \frac{\overbrace{n(n-1)(n-2)\cdots(n-(k-1))}^{k}(n-k)!}{(n-k)!} \\ \\ &=&\displaystyle\overbrace{n(n-1)(n-2)\cdots(n-(k-1))}^{k} \end{array}
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n&=& \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \frac{n!}{(n-k)!}\times \frac{1}{n^k} \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \frac{\overbrace{n(n-1)(n-2)\cdots(n-(k-1))}^{k}}{n^k} \\ \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \frac{\overbrace{n(n-1)(n-2)\cdots(n-(k-1))}^{k}}{\underbrace{n\times n\times n\times \cdots \times n}_k} \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \frac{n}{n}\frac{n-1}{n}\frac{n-2}{n}\cdots\frac{n-(k-1)}{n} \\ \\ \\ &=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
とりあえず
このような「比較できそうな式」には辿り着けますが
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n&=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
これが本当に役に立つのか
それはこの時点ではまだ分かりません。
単調増加である
とりあえず n を増やして比較してみると
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n&=& \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
n+1 の場合は ↓ の数が加算される
\begin{array}{llllll} \displaystyle \frac{1}{(n+1)!}\overbrace{1\left(1-\frac{1}{n+1} \right)\left(1-\frac{2}{n+1} \right) \cdots \left(1-\frac{(n+1)-1}{n+1} \right)}^{n+1} \end{array}
これを除けば
n 個の ↓ の項の個数は変わらない
\begin{array}{llllll} \displaystyle \frac{1}{k!}\overbrace{1\left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right)}^{k} \end{array}
これが
整理できる「 a_n と a_{n+1} の違い」ですから
\begin{array}{rcrllllll} \displaystyle \frac{1}{n}&\textcolor{skyblue}{>}&\displaystyle \frac{1}{n+1} \\ \\ \displaystyle 1- \frac{1}{n}&\textcolor{pink}{<}&\displaystyle 1-\frac{1}{n+1} \end{array}
後は直感的に
「分母が大きい方が小さい」
という明らかな事実を考慮すれば
\begin{array}{llllll} \displaystyle a_{n+1}-a_n \end{array}
この比較は
\begin{array}{llllll} \displaystyle a_n&=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \overbrace{1 \left(1-\frac{1}{n} \right) \cdots \left(1-\frac{k-1}{n} \right)}^{k} \\ \\ a_{n+1}&=&\displaystyle \sum_{k=0}^{\textcolor{pink}{n+1}} \frac{1}{k!} \times \overbrace{1 \left(1-\frac{1}{n+1} \right) \cdots \left(1-\frac{k-1}{n+1} \right)}^{k} \\ \\ &=&\displaystyle \sum_{k=0}^{\textcolor{skyblue}{n}} \frac{1}{k!} \times \overbrace{1 \left(1-\frac{1}{n+1} \right) \cdots \left(1-\frac{k-1}{n+1} \right)}^{k}+α \end{array}
\begin{array}{llllll} \displaystyle α&=&\displaystyle \frac{1}{(n+1)!}\overbrace{1\left(1-\frac{1}{n+1} \right) \cdots \left(1-\frac{(n+1)-1}{n+1} \right)}^{n+1} \end{array}
こうなので
\begin{array}{llllll} \displaystyle a_n&=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \overbrace{1 \left(1-\frac{1}{n} \right) \cdots \left(1-\frac{k-1}{n} \right)}^{k} \\ \\ a_{n+1}-α&=&\displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times \overbrace{1 \left(1-\frac{1}{n+1} \right) \cdots \left(1-\frac{k-1}{n+1} \right)}^{k} \end{array}
\begin{array}{llllll} \displaystyle a_n&<&a_{n+1}-α \end{array}
この大小比較と
\begin{array}{llllll} \displaystyle α&=&\displaystyle \frac{1}{(n+1)!}\overbrace{1\left(1-\frac{1}{n+1} \right) \cdots \left(1-\frac{(n+1)-1}{n+1} \right)}^{n+1} \end{array}
\begin{array}{llllll} \displaystyle 0&<&\displaystyle 1-\frac{1}{n+1} \end{array}
これが明らかに「正の値」であることから
\begin{array}{llllll} \displaystyle &&a_n&<&a_{n+1}-α \\ \\ &&α&<&a_{n+1}-a_n \\ \\ \\ 0&<&α&<&a_{n+1}-a_n \\ \\ 0&& &<&a_{n+1}-a_n \end{array}
これが明らかであると分かるので
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n \end{array}
結果、これは「単調増加」であると言えます。
ちょっと複雑ですが
まあこれはすぐに分かると思います。
有界である
問題はどちらかと言えばこっち
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n &<&? \end{array}
単調増加であることは分かりました。
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n&=&\infty &&? \end{array}
なので「増え続ける」ことは確かですが
だからこそ「発散する」可能性を潰せてはいません。
なので「収束する」と考えるなら
『上限の存在』を考える必要があるわけですが
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n&=& \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
なんか大変そうです。
でもこれ
実はわりとすぐに分かるんですよ。
\begin{array}{llllll} \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
というのもこの式変形から
\begin{array}{llllll} \displaystyle 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
\begin{array}{llllll} \displaystyle 1-\frac{1}{n}&<1& \end{array}
これが 1 より下なのは明らかですから
\begin{array}{llllll} \displaystyle \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) &≤&\displaystyle\sum_{k=0}^{n} \frac{1}{k!} \end{array}
間違いなくこうだと言える。
\begin{array}{llllll} \displaystyle\sum_{k=0}^{n} \frac{1}{k!}&≤&\displaystyle 1+\sum_{k=0}^{n} \frac{1}{2^k} \end{array}
\begin{array}{rllllll} \displaystyle\sum_{k=0}^{n} \frac{1}{k!}&=&\displaystyle \frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!} +\cdots \\ \\ &=&\displaystyle 1+1+\frac{1}{2}+\frac{1}{2\times 3}+\cdots \\ \\ \\ \displaystyle 1+\sum_{k=0}^{n} \frac{1}{2^k} &=&\displaystyle 1+\frac{1}{2^0}+\frac{1}{2^1}+\frac{1}{2^2}+\cdots\\ \\ &=&\displaystyle 1+1+\frac{1}{2}+\frac{1}{2\times 2}+\cdots \end{array}
そしてこれもまた上から抑えられるので
\begin{array}{rlclllll} \displaystyle \sum_{k=0}^{n} \frac{1}{2^k}&=&\displaystyle \frac{\displaystyle 1-\frac{1}{2^n}}{\displaystyle 1-\frac{1}{2}} \\ \\ \displaystyle \lim_{n\to \infty}\sum_{k=0}^{n} \frac{1}{2^k}&=&\displaystyle \frac{\displaystyle 1}{\displaystyle 1-\frac{1}{2}} \\ \\ &=&\displaystyle\frac{1}{\displaystyle\left(\frac{1}{2}\right)} \\ \\ &=&2 \\ \\ \\ \displaystyle 1+\sum_{k=0}^{n} \frac{1}{2^k}&≤&3 \end{array}
これが「上界」の要素として導ける。
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n&≤&3 \end{array}
ということは
「上限の具体的な値」は分かりませんが
「上に有界である」ことは確かなことだと分かる。
結果
「単調増加」かつ「有界」なので
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n \end{array}
こいつは「収束する」と言えます。
指数関数の微分とネイピア数
指数関数の「微分」を考えると
\begin{array}{llllll} \displaystyle \left( a^x \right)^{\prime}&=&\displaystyle \lim_{h\to 0}\frac{a^{x+h}-a^x}{(x+h)-x} \\ \\ &=&\displaystyle \lim_{h\to 0}\frac{a^x(a^h-1)}{h} \\ \\ \\ &=&\displaystyle a^x\lim_{h\to 0}\frac{a^h-1}{h} \end{array}
これではうまくいきませんが
好きにとれる『任意の実数 a 』を調整して
以下のような「定数 e 」を定めると
(ネイピア数のオイラーの定義)
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{e^h-1}{h}&=&1 \end{array}
「対数関数」を使えば
\begin{array}{rcrllllll} \displaystyle a^x&=&\displaystyle e^{\log a^x} \\ \\ \displaystyle \frac{d}{dx} a^x&=&\displaystyle \frac{d}{dx} e^{\log a^x} \\ \\ &=&\displaystyle (\log a^x)^{\prime}e^{\log a^x} \\ \\ &=&\displaystyle a^x \log a \end{array}
「指数関数の微分」は
このように求めることができます。
オイラーの定義の欠点
以下の式はいわゆる「不定形」です。
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{a^h-1}{h} \end{array}
更に言うなら
「ロピタルの定理」を用いても
\begin{array}{llllll} \displaystyle \frac{d}{dx}a^x&=&\displaystyle a^x\lim_{h\to 0}\frac{a^h-1}{h} \end{array}
こいつが必ずこの形になりますから
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{a^h-1}{h} \end{array}
簡単にはこいつを排除できません。
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{a^h-1}{h}&=&? \end{array}
そしてこいつは収束する保証がないため
この時点で操作はストップ。
もうどうにもなりません。
これがこの定義のちょっと曖昧な点で
\begin{array}{llcllll} \displaystyle \lim_{h\to 0}\frac{a^h-1}{h}&=&α &&? \\ \\ \displaystyle \lim_{h\to 0}\frac{e^h-1}{h}&=&1 && ? \end{array}
こいつが収束することを前提のように扱っている
この点がちょっと良くないんですよ。
(循環定義に陥る)
欠点解消の試み
これが「収束する」かどうかは示せませんが
『収束するだろう』ことは示すことができます。
\begin{array}{llllll} \displaystyle h(x)&=&\displaystyle\frac{a^x-1}{x} \end{array}
というのも
a を調整しさえすれば
\begin{array}{llllll} \displaystyle \displaystyle\frac{1^x-1}{x}&=&0 \end{array}
例えばもっとも単純なパターンでは
これは常に 0
\begin{array}{llllll} \displaystyle \lim_{x\to 0-0} \frac{1^x-1}{x}&=&0&=&\displaystyle \lim_{x\to 0+0} \frac{1^x-1}{x} \end{array}
更には x=0 で連続であると言えるので
このパターンでは間違いなく「収束」します。
\begin{array}{lcccccccc} \displaystyle h(-2)&=&\displaystyle\frac{2^{-2}-1}{-2} &=&\displaystyle\frac{3}{8} \\ \\ \displaystyle h(-1)&=&\displaystyle\frac{2^{-1}-1}{-1}&=&\displaystyle\frac{1}{2} \\ \\ \\ \displaystyle h(1)&=&\displaystyle\frac{2-1}{1}&=&1 \\ \\ \displaystyle h(2)&=&\displaystyle\frac{2^2-1}{2}&=&\displaystyle\frac{3}{2} \end{array}
他にも
例えば a>1 であるなら
これはほぼほぼ間違いなく増加し続ける関数
\begin{array}{cccccccccccccc} \displaystyle h(-2)&<&h(-1)&<&?&<&h(1)&<&h(2) \end{array}
つまり
「単調増加」を『仮定』できる関数なので
(微分はまだできないので変化率は不明)
\begin{array}{llllll} \displaystyle -2&<&x&<&2 \end{array}
\begin{array}{llrllll} \displaystyle h(-2)&<&\displaystyle\frac{2^x-1}{x}&<&h(2) \\ \\ \displaystyle h(-2)&<&\displaystyle\lim_{x\to 0}\frac{2^x-1}{x}&<&h(2) \end{array}
「点 0 周り」が「上に有界」である
これを『仮定の元では』保証できます。
\begin{array}{llllll} \displaystyle h(-0.001)&=&0.69290 \, 70095 \, 47478 \, 07762 \, 06446 \, 36498 \, \cdots \\ \\ h(0.001)&=&0.69338 \, 74625 \, 80632 \, 53756 \, 86393 \, 03859 \, \cdots \end{array}
\begin{array}{llllll} \displaystyle 0.69289&<&\displaystyle\lim_{x\to 0}\frac{2^x-1}{x}&<&0.69339 \end{array}
加えてこの操作はどこまでも可能
つまり連続性があるように見えるので
\begin{array}{llllll} \displaystyle h(0-δ)&<&\displaystyle\lim_{x\to 0}\frac{2^x-1}{x}&<&h(0+δ) \end{array}
「収束しそう」だという根拠は多いです。
(1点に定まる保証がまだ無い)
ネイピア数の導出
ネイピア数 e それ自体は
いろんな方法で求めることができます。
\begin{array}{lclllllll} \displaystyle e&=&\displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n \\ \\ e^x&=&\displaystyle e^x\lim_{h\to 0} \frac{e^h-1}{h} \end{array}
ただこのままではいろいろとあれです。
なんか抽象的で分かりにくい。
よく分からない定数
厳密な定義については語った通りですが
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n&≤&3 \end{array}
\begin{array}{rccllllll} \displaystyle \frac{d}{dx} \log_c x&=&\displaystyle \left( \log_c e\right) \frac{1}{x} \\ \\ \left( \log_c e \right)&=&\displaystyle \int_{1}^{e} \left(\log_c e \right) \frac{1}{x} \,dx \\ \\ &=&\log_c e - \log_c 1 \end{array}
\begin{array}{llcllll} \displaystyle \log_c e&=&? \\ \\ \log_e e&=&1 \end{array}
このやり方で出てきたこれが
\begin{array}{llllll} \displaystyle \lim_{n\to \infty} \left(1+ \frac{1}{n} \right)^n&≤&\displaystyle\lim_{n\to \infty}\sum_{k=0}^{n} \frac{1}{k!} \end{array}
オイラーの定義の e と一致するのか。
その辺りの話に付いてはまだ触れていません。
これは一応
\begin{array}{llllll} \displaystyle \left(1+ \frac{1}{n} \right)^n&=& \displaystyle \sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}1 \left(1-\frac{1}{n} \right)\left(1-\frac{2}{n} \right) \cdots \left(1-\frac{k-1}{n} \right) &=&1 \end{array}
「下から」も抑えられるので
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\sum_{k=0}^{n} \frac{1}{k!} \times 1 \left(1-\frac{1}{n} \right) \cdots \left(1-\frac{k-1}{n} \right)&=&\displaystyle \lim_{n\to\infty}\sum_{k=0}^{n}\frac{1}{k!} \end{array}
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}\sum_{k=0}^{n}\frac{1}{k!}&=&\displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n \end{array}
式変形はできるんですが
この時点ではまだ指数関数の微分には繋がりません。
\begin{array}{llllll} \displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n&=&\displaystyle 1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots \end{array}
最終的に収束することは分かっている
そんな具体的な値が求まるのみです。
(まあこの時点でだいたい分かる)
微分で変化しない関数
というわけで
『オイラーの定義』について確認してみると
\begin{array}{rllllll} \displaystyle \frac{d}{dx}e^x&=&e^x \\ \\ \left( e^x \right)^{\prime}&=&e^x \\ \\ \\ \left( e^x \right)^{(1)}&=&e^x \\ \\ \left( e^x \right)^{(n)}&=&e^x \end{array}
\begin{array}{llllll} \displaystyle \lim_{h\to 0} \frac{e^h - 1}{h}&=&1 \end{array}
まあこうなんですが
\begin{array}{llllll} \displaystyle \lim_{h\to 0} \frac{e^h - 1}{h}&=&1 \end{array}
この部分がどうにもならないので
とりあえず式変形しないことには
具体的な話はできない感じがします。
ちなみにこの時点では
ここで定義される e もまた
「自然対数の底」と一致するかは不明です。
マクローリン展開による e の導出
式変形の方法はいろいろありますが
\begin{array}{llllll} f(x)&=&\displaystyle f(0)+f^{(1)}(0)x^1 +\frac{1}{2!}f^{(2)}(0)x^2+\cdots \\ \\ &=&\displaystyle \sum_{n=0}^{\infty}\frac{1}{n!}f^{(n)}(0)x^n \\ \\ \\ \displaystyle e^x&=&\displaystyle e^0+e^0x^1 +\frac{1}{2!}e^0x^2+\cdots \\ \\ &=&\displaystyle \sum_{n=0}^{\infty}\frac{1}{n!}e^0x^n \\ \\ &=&\displaystyle e^0\sum_{n=0}^{\infty}\frac{1}{n!}x^n \end{array}
自然対数の底の形に似ているので
「マクローリン展開」を採用してみます。
\begin{array}{llllll} \displaystyle e^x&=&\displaystyle 1+\frac{1}{1!}x^1+\frac{1}{2!}x^2 +\frac{1}{3!}x^3+\cdots \\ \\ \\ e^1&=&\displaystyle 1+\frac{1}{1!}1^1+\frac{1}{2!}1^2 +\frac{1}{3!}1^3+\cdots \\ \\ e&=&\displaystyle 1+\frac{1}{1!}+\frac{1}{2!} +\frac{1}{3!}+\cdots \\ \\ &=&\displaystyle\sum^{\infty}_{k=0}\frac{1}{k!} \end{array}
するとまあだいたい想像通り
このような綺麗な形が導けるので
一気に結論まで近づいてしまいました。
変な定数の一致
以上の情報を整理すると
\begin{array}{llllll} \displaystyle \lim_{h\to 0}\frac{e^h - 1}{h}&=&1 \end{array}
\begin{array}{cllllll} e&=& \displaystyle \textcolor{skyblue}{ \lim_{n\to\infty } \sum^{n}_{k=0}\frac{1}{k!} } \\ \\ \displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n &=&\displaystyle \textcolor{pink}{ \lim_{n\to \infty}\sum_{k=0}^{n} \frac{1}{k!} } \end{array}
こんな関係が導かれるわけですが
\begin{array}{llllll}\textcolor{skyblue}{ \displaystyle \lim_{n\to\infty } \sum^{n}_{k=0}\frac{1}{k!} }&=&\displaystyle \textcolor{pink}{ \lim_{n\to \infty}\sum_{k=0}^{n} \frac{1}{k!} }\end{array}
\begin{array}{llllll} \displaystyle e&=&\displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n \end{array}
これ、明らかに同じですよね。
もうどう見ても同じ。
というわけで以上
「ネイピア数」についてはこんな感じ。
\begin{array}{llllll} \displaystyle e&=&\displaystyle \lim_{n\to\infty} \left(1+ \frac{1}{n} \right)^n \end{array}
ちょっと複雑ですが
以上の流れを辿れば
これらが一致することがわかります。
