|| 収束すると同値の条件を持つ数列のこと
基本列と呼ばれるほど基礎的な数列
収束の判定で最終的に行き着くとこです。
スポンサーリンク
目次
基本列「1つの値に寄っていく数列」
基本列 Cauchy Sequence
|| 収束すると同値の条件を持つ数列
「数の差が減っていく」「収束する」を意味する。
\begin{array}{llllll} \displaystyle \forall ε &∃N>0 & \forall n>N &\forall m>N \end{array}
\begin{array}{llllll} \displaystyle N≤n,m &&⇒&&|a_n-a_m|<ε \\ \\ n,m \to \infty &&⇒&&\displaystyle |a_n-a_m|\to 0 \end{array}
\begin{array}{llllll} \displaystyle \lim_{n,m\to \infty}|a_n-a_m|&=&0 \end{array}
条件は以上の通り。
これを満たす「数列 \{a_n\} 」を
「基本列・コーシー列」と言います。
条件の意味
(N<)n,m が大きくなっていくと
a_n-a_m が 0 に近づいていく
\begin{array}{llllll} \displaystyle \lim_{n,m\to \infty}|a_n-a_m|&=&0 \end{array}
数式の意味はそんな感じで
これは「最終的に1つの値に寄っていく」
ということを遠回しに意味しています。
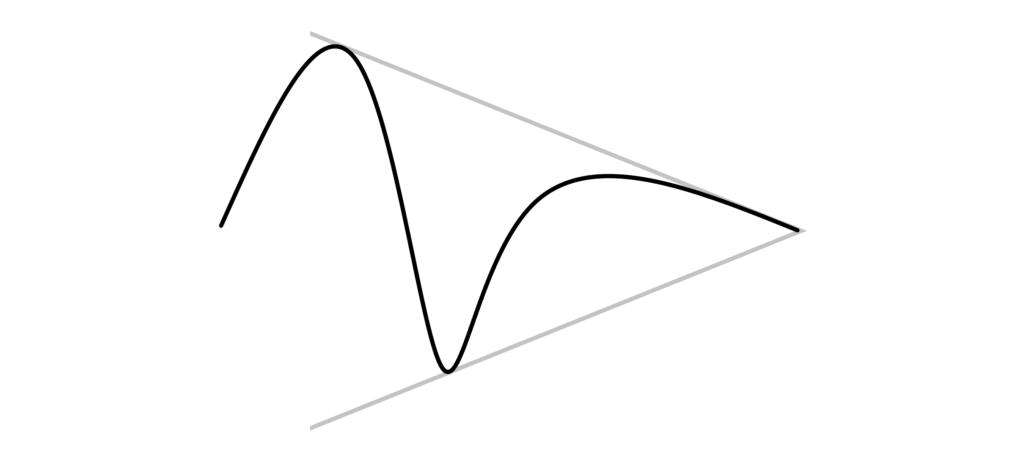
イメージはこんな感じですね。
上の灰色線 a_n と下の灰色線 a_m
\begin{array}{llllll} n,m \to \infty &&⇒&&\displaystyle |a_n-a_m| \to 0 \end{array}
n,m が増えるとこの差 a_n-a_m がどんどん小さくなる。
いやほんと、そのままです。
極限の不定形と基本列
「極限」の操作で多く出てくる
以下の形のものは基本的に定義できません。
\begin{array}{llllll} \displaystyle \frac{0}{0}&&&&\displaystyle\frac{x^2+1}{x^2-1} &\displaystyle\frac{\sin x}{x} \\ \\ \displaystyle \frac{\infty}{\infty}&&&&\displaystyle\frac{x^2+1}{x^2-1} &\displaystyle\frac{e^x}{x} \\ \\ 0\times\infty &&&&\displaystyle (x^2+1)\frac{1}{x^2-1} &\displaystyle\sin x\frac{1}{x} \\ \\ \infty - \infty &&&& \displaystyle e^x-x^n & a^x - x^a \end{array}
「この形にならないよう式を変形」したり
「ロピタルの定理」などを考えれば
\begin{array}{llllll} \displaystyle \lim_{x\to 0}\frac{f(x)}{g(x)}&=&\displaystyle \lim_{x\to 0}\frac{f^{\prime}(x)}{g^{\prime}(x)} \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \frac{0}{0}&&\displaystyle \frac{\infty}{\infty} && \end{array}
この形でも大丈夫なことはありますが
基本的に ↓ の形はよく分からないので定義不可
\begin{array}{llllll} \displaystyle \infty - \infty \end{array}
\begin{array}{llllll} \displaystyle \infty - \infty&=&? \\ \\ \infty - (-\infty)&=&\infty \\ \\ -\infty -\infty&=&-\infty \end{array}
つまり \infty - \infty の形が出てくると
\begin{array}{llllll} \displaystyle a_n-a_m&=&α±\infty \\ \\ &=&±\infty \\ \\ \\ a_n-a_m&=&\pm \infty \mp\infty \\ \\ &=&? \end{array}
これらのパターンはこのようになり
\begin{array}{llllll} \displaystyle \lim_{n,m\to \infty}|a_n-a_m|&=&0 \end{array}
『どのように n,m をとっても』
「常に N(<n,m) が存在する」とは言えません。
\begin{array}{llllll} \displaystyle \forall ε &∃N>0 & \forall n>N &\forall m>N \end{array}
\begin{array}{llllll} \displaystyle N≤n,m &&⇒&&|a_n-a_m|<ε \end{array}
つまりこの条件を満たすとき
『 a_n と a_m はどちらも ±\infty にならない』
\begin{array}{llllll} \displaystyle a_{10^{10}}&=&\infty \end{array}
\begin{array}{llllll} \displaystyle |a_{10^{10}+1}-a_{10^{10}}|&=&\infty &&〇\\ \\ |a_{10^{10}+1}-a_{10^{10}}|&<&ε &&× \end{array}
とまあこのようになるため
「 a_n が無限になる」という可能性を
この条件 |a_n-a_m|<ε は排除できます。
\begin{array}{llllll} \displaystyle |a_n-a_m|&<&\infty \end{array}
ちなみに ε が無限でも
|a_n-a_m| の値は有限になります。
具体的な感じ
代表的な例で確かめてみます。
使うのは「絶対値」の感覚だけ。
\begin{array}{llllll} \displaystyle a_n&=&\displaystyle\frac{1}{n} \end{array}
\begin{array}{llllll} \displaystyle |a-b|&=&|a+(-b)| \\ \\ &&|a+(-b)|&≤&|a|+|-b| \\ \\ &&&&|a|+|-b|&=&|a|+|b| \end{array}
\begin{array}{llllll} \displaystyle \left|\frac{1}{n}-\frac{1}{m}\right|&≤&\displaystyle \left|\frac{1}{n}\right|+\left|\frac{1}{m}\right| \end{array}
\begin{array}{llllll} \displaystyle N&≤&n,m \\ \\ \displaystyle \frac{1}{N}&≥&\displaystyle \frac{1}{n},\frac{1}{m} \end{array}
\begin{array}{llllll} \displaystyle \left|\frac{1}{n}-\frac{1}{m}\right|&≤&\displaystyle \left|\frac{1}{n}\right|+\left|\frac{1}{m}\right| &≤& \displaystyle \frac{1}{N}+\frac{1}{N} \end{array}
ここまで分かれば後は簡単
適当な ε>0 を用意すれば
\begin{array}{llllll} \displaystyle \frac{1}{N}+\frac{1}{N}&<&ε \end{array}
\begin{array}{llllll} \displaystyle \left|\frac{1}{n}-\frac{1}{m}\right|&<&ε \end{array}
すぐに条件を満たすことが分かります。
\begin{array}{llllll} \displaystyle a_n&=&\displaystyle\frac{1}{n} \end{array}
つまりこの数列 a_n は基本列
ただこれだけじゃあれなので
「発散する」場合のパターンを考えてみると
\begin{array}{llllll} \displaystyle u_n&=&n \end{array}
例えばこれは「差 |n-m| が必ず 1 以上」
\begin{array}{llllll} \displaystyle N&≤&n,m \\ \\ N&≤&N+1,N+2 \end{array}
\begin{array}{llllll} \displaystyle |(N+1)-(N+2)|&=&1 \end{array}
\begin{array}{llllll} \displaystyle 1&≤&|u_n-u_m|&<&ε \\ \\ 1&&&<&ε \end{array}
つまり 0<ε≤1 の範囲はとれないので
∀ε>0 の条件を満たせない。
だからこれはコーシー列とは言えません。
\begin{array}{llllll} \displaystyle t_{n}&=&(-1)^n \end{array}
\begin{array}{llllll} \displaystyle |(-1)^{N+1}-(-1)^{N+2}|&=&|-1-1|&=&2 \\ \\ &=&|1-(-1)|&=&2 \end{array}
「振動する」パターンも同様。
ε の範囲に問題が生じます。
以上、コーシー列・基本列の判定はこんな感じ。
確認してみると当然の話しかしてません。
収束するやつは基本列
「収束する」ということがどういうことか。
まず定義を確認しておくと
\begin{array}{llllll} \displaystyle \lim_{n\to\infty}a_n&=&α \end{array}
\begin{array}{llllll} \displaystyle |a_n-α|&<&ε \end{array}
当然の話ではありますが
「極限値 α が存在する」ということだと分かります。
\begin{array}{llllll} \displaystyle |a_n-a_m|&<&ε_{h} &&&? \end{array}
で、「収束する」→「基本列である」を示すには
ここから「基本列」を導かなければならないわけで
\begin{array}{llllll} \displaystyle |a_n-a_m|&=&|a_n-α+α-a_m| \\ \\ &=& \left| a_n-α-(a_m-α) \right| \end{array}
以上、出揃っている条件から
「 ε より小さい」と分かる形と
「三角不等式」の存在を考慮すれば
\begin{array}{llllll} \displaystyle \left|a_n-α+α-a_m \right|&≤&\left| a_n-α \right|+\left| α-a_m \right| \\ \\ &=&\left| a_n-α \right|+\left| a_m-α \right| \end{array}
\begin{array}{llllll} \displaystyle \left| a_n-α \right|&<&ε_n \\ \\ \displaystyle \left| a_m-α \right|&<&ε_m \end{array}
\begin{array}{llllll} \displaystyle \displaystyle \left|a_n-α+α-a_m \right|&≤&\left| a_n-α \right|+\left| a_m-α \right| &<&ε_n+ε_m \end{array}
このような関係が導けるので
\begin{array}{llllll} \displaystyle \displaystyle |a_n-a_m|&<&ε_n+ε_m \\ \\ &&ε_n+ε_m&=&ε \end{array}
結果として
\{a_n\} は「収束する」という前提から
\{a_n\} は「基本列である」を導けることから
\begin{array}{llllll} \displaystyle |a_n-α|<ε &&⇒&&\displaystyle |a_n-a_m|<ε \end{array}
「収束する」ということは
「基本列である」と言える、と
まあこんな感じでこれは示すことができます。
基本列は収束する
実は ↑ の逆であるこれは成立し
「基本列である」と「収束する」
これが同値だと分かるんですけど
\begin{array}{llllll} \displaystyle |a_n-α|<ε &&⇐&&\displaystyle |a_n-a_m|<ε \end{array}
こちらの方の証明には
『極限値を取り出す』という工程で
「Bolzano-Weierstrass の定理」が必要になります。
\begin{array}{llllll} \displaystyle \displaystyle |a_n-a_m|&<&ε \end{array}
というのもこの時点では「極限値の存在」は不明
「有界である」ことくらいは分かりますが
その他のことについてはよく分かりません。
数列が有界である
定義を確認しておきます。
\begin{array}{llllll} \displaystyle m&≤&a_n&≤&M \end{array}
a_n に対して |a_n|<M となる
そんな M(>0) が「 n がなんであれ」存在すること
\begin{array}{llllll} \displaystyle |a_n|&<&M \end{array}
これが「有界」の定義なんですが
当たり前の話なので特に深堀することはありません。
基本列は有界である
「コーシー列」の定義を確認しておくと
『 n,m が大きくなると差が 0 に近くなる』
\begin{array}{llllll} \displaystyle |a_n-a_m|&<&ε \end{array}
言い換えると
好きに ε(>0) をとると
条件 |a_n-a_m|<ε を満たす N(<n,m) が必ず存在する
とまあそんな感じですから
|a_n-a_m| が有限の範囲である以上
「有界である」ことはほぼ明らか
\begin{array}{llllll} \displaystyle K&<&a_n&<&M \end{array}
ということはつまり
『どの a_n よりもでかい有限の M 』
『どの a_n よりも小さい有限の K 』
\begin{array}{llllll} \displaystyle &&&& a_n&≤&M&<&\infty \\ \\ -\infty&<&K&≤&a_n \end{array}
これらが導けるはず
ということが直感的にすぐわかります。
\begin{array}{llllll} \displaystyle \max\{1,5,0\}&=&5 \end{array}
以下、最大値を取り出すために
こういう \max 最大値を取り出す記号を使います。
有界の定義に寄せていく
「有界である」に近付けるため
「基本列」の定義から a_n を取り出してみます。
\begin{array}{llcllll} \displaystyle &&|a_n-a_m|&<&ε \\ \\ \displaystyle -ε&<&a_n-a_m&<&ε \end{array}
\begin{array}{llllll} \displaystyle a_m-ε&<&a_n&<&a_m+ε \end{array}
するとこうなることから
a_n は a_m+ε で上から抑えられる
a_n は a_m-ε で下から抑えられる
これが明らかな事実として導けます。
\begin{array}{llllll} \displaystyle \displaystyle a_m-ε&<&a_n&<&a_m+ε \end{array}
で、これが明らかな以上
a_m\pm ε を上下から抑えられるような
そんな都合の良い定数 K,M が分かれば
\begin{array}{llllll} \displaystyle K&≤&a_m-ε&<&a_n \\ \\ &&&&a_n&<&a_m+ε&≤&M \end{array}
「有界である」ということが示せるので
\begin{array}{llllll} \displaystyle M_{\mathrm{all}}&=&\max\{a_0,a_1,a_2,\cdots,a_k,\cdots\} \\ \\ K_{\mathrm{all}}&=&\min\{a_0,a_1,a_2,\cdots,a_k,\cdots\} \end{array}
\begin{array}{llllll} \displaystyle M&=&\max\{a_0,a_1,a_2,\cdots,a_k\} \\ \\ K&=&\min\{a_0,a_1,a_2,\cdots,a_k\} \end{array}
ここでこのような形で
『数列の一部を切り取る』操作を行い
\begin{array}{llllll} \displaystyle N&≤&n,m \end{array}
\begin{array}{llllll} \displaystyle M&=&\max\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}\} \\ \\ K&=&\min\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}\} \end{array}
N<m=N+1 のような形で定義して
「後者 a_{n+1}=f(a_n) 」を得られるようにした後
\begin{array}{llllll} \displaystyle M&=&\max\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}+ε\} \\ \\ K&=&\min\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}-ε\} \end{array}
確実に a_n と大小比較できるよう
a_m ( a_{N+1} )に ε を付け足し
「最大値」「最小値」を定めて
\begin{array}{llllll} \displaystyle M&=&\max\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}+ε\} \\ \\ K&=&\min\{a_0,a_1,a_2,\cdots,a_{N},a_{N+1}-ε\} \end{array}
\begin{array}{llllll} \displaystyle n,m&&→&&N \\ \\ &&→&&m&&→&&m=N+1 \end{array}
これが『 N がなんであれ定義できる』上に
n,m がなんであっても常に定義可能であることから
\begin{array}{llllll} \displaystyle &&a_{N+1}+ε&=&a_m+ε&≤&M \\ \\ K&≤&a_{N+1}-ε&=&a_m-ε \end{array}
K,M は確実に存在するため
最大値と最小値の定義からこれが求められて
\begin{array}{llllll} \displaystyle \displaystyle a_m-ε&<&a_n&<&a_m+ε \end{array}
最後に「基本列・コーシー列」の定義から
最初に求めたこれも明らかですから
\begin{array}{llllll} \displaystyle K&≤&a_m-ε&<&a_n&<&a_m+ε&≤&M \end{array}
結果としてこうなる。
\begin{array}{llllll} \displaystyle K&<&a_n&<&M \end{array}
つまり「有界である」ということが
こうすれば確実に求められます。
有界なら収束する部分列が存在する
「基本列」が「有界である」ということは
「Bolzano-Weierstrass の定理」より
『収束する部分列 \{a_{H(n)}\} が存在する』ということ。
\begin{array}{llllll} \displaystyle \lim_{H(n)\to \infty}a_{H(n)}&=&α \end{array}
つまり結果として
「極限値 α の存在」が導かれるので
\begin{array}{llllll} \displaystyle |a_n-a_m|&=&|a_n-a_{H(n)}|&<&ε_c \\ \\ &&|a_{H(n)}-α|&<&ε_w \end{array}
「コーシー列」と「部分列」の定義から
「三角不等式」を用いると
\begin{array}{llllll} \displaystyle |a_n-α|&≤&|a_n-a_{H(n)}|+|a_{H(n)}-α|&& \\ \\ &&|a_n-a_{H(n)}|+|a_{H(n)}-α|&<&ε_c+ε_w \end{array}
\begin{array}{llllll} \displaystyle |a_n-α|&<&ε \end{array}
「 a_n は α に収束する」を導くことができる。
とまあこんな感じで
「基本列である」→「収束する」は導けます。
以上
「収束する」→「基本列である」
「基本列である」→「収束する」
\begin{array}{llllll} \displaystyle |a_n-α|<ε &&⇒&&\displaystyle |a_n-a_m|<ε \\ \\ \displaystyle |a_n-α|<ε &&⇐&&\displaystyle |a_n-a_m|<ε \end{array}
これが導かれたので
「基本列だ」と「収束する」は『同値』である
ということが示されました。
