基底とかいう線形代数学の核になる概念についてできるだけ分かりやすくまとめてみた

|| 次元を厳密に定義するためのもの

「ベクトル」の主な役割の１つになります。

ベクトル Vector

この記事は「ベクトル」を知らないと

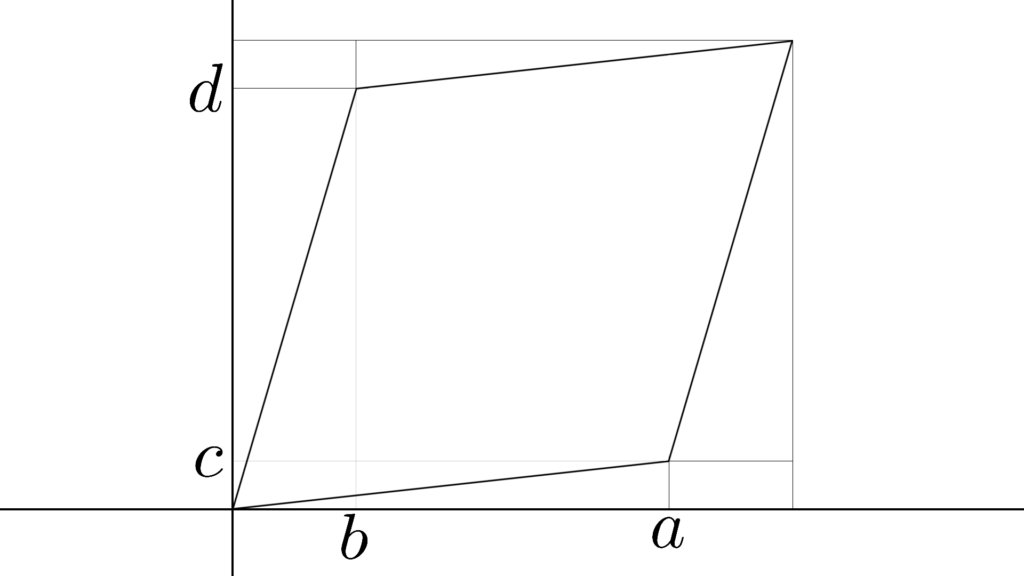
$\begin{array}{lcl} v_1&=&(a,c) \\ \\ v_2&=&(b,d) \end{array}$

だいぶ分からない内容になっています。

線型空間 Linear Space

これは「ベクトル」を問題なく使える保証のことで

$\begin{array}{cccccc} \displaystyle v,u,w&∈&V &&V \,\, \mathrm{is} \,\, \mathrm{Set \,\, of \,\, Vector} \\ \\ a,b&∈&S &&S \,\, \mathrm{is} \,\, \mathrm{Scalar \,\, Field} \end{array}$

「ベクトルの振る舞い」をまとめたものになります。

$\begin{array}{cccccccc} \displaystyle (v+u)+w&=&v+(u+w) &&\mathrm{Associative} \\ \\ v+u&=&u+v &&\mathrm{Commutative} \\ \\ \\ v+\vec{0}&=&v&&\mathrm{Identity} \\ \\ v+(-v)&=&0 &&\mathrm{Inverse} \\ \\ \\ a\times (b\times v)&=&(a\times b)\times v&&\mathrm{Associative} \\ \\ 1\times v&=&v&&\mathrm{Identity} \\ \\ \\ a\times (v+u)&=&a\times v+a\times u&&\mathrm{Distributive} \\ \\ (a+b)\times v&=&a\times v+b\times v&&\mathrm{Distributive} \end{array}$

$\begin{array}{llllll} \displaystyle (V,+,\times) \,\, \mathrm{is} \,\, \mathrm{Vector \,\, Space} \,\, \mathrm{on} \,\, S \end{array}$

詳細は本題から逸れるので

この記事ではあまり詳しく扱いません。

（より詳しくは線型空間の記事で）

線形空間の基本的な性質

この記事で出てくる性質については

厳密な証明で必要になるためまとめておきます。

$\begin{array}{ccc} \vec{0} &\in& V \\ \\ 0,1 &\in& S \end{array}$

まず「単位元」についてですが

これは「全てのベクトル空間」でこうなります。

（ $S$ は体 $\mathrm{Field}$ であるためこうなる）

↑ で紹介した内容は要はそういうことで

（先に記述したのはざっくりとした法則だけ）

$\begin{array}{rcr} v,u \in V &\to& v+u \in V \\ \\ v \in V&\to& -v \in V \end{array}$

「加法」も「スカラーとの乗法」も

$\begin{array}{ccc} c\in S∧v\in V &\to& cv \in V \end{array}$

「公理」により

「全て $V$ に含まれる」ことになっています。

（ $S$ はだいたい実数全体 $R$ をとります）

線型性 Linearity

「加法」「斉次性」で定義される性質のこと

$\begin{array}{ccc} f(ax)&=&af(x) && 斉次性 \\ \\ f(x+y)&=&f(x)+f(y) && 加法性 \\ \\ \\ f(ax+by)&=&af(x)+bf(y) && 線型性 \end{array}$

要は「内積」の感覚で

$\begin{array}{llllll} \displaystyle ax+by &→&(a,b)(x,y) \\ \\ ax+by+cz &→&(a,b,c)(x,y,z) \end{array}$

$\begin{array}{cccc} \displaystyle a_0 x^0 + a_1 x^1 + a_2 x^2 + \cdots + a_n x^n &=&0 \\ \\ x_1 p_1 + x_2 p_2 + x_3 p_3 + \cdots + x_np_n &=&E(X) \end{array}$

よく見るこの形のことを言っています。

（見た目一直線だから線型）

線型独立 Linearly Independent

|| ベクトルが一直線上に無い感じ

「次元」を増やさないと説明できない状態

$\begin{array}{ccc} v_1,v_2,v_3,...,v_n&\in&\mathrm{Vector} \\ \\ c_1,c_2,c_3,...,c_n&\in&\mathrm{Scalar} \end{array}$

$\begin{array}{ccccc} \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} &&→&& c_1=c_2=\cdots=c_n=0 \end{array}$

一般的にはこんな感じで

（ $v_n$ は零ベクトル $\vec{0}$ ではないとします）

「平面」の話だと

$\begin{array}{ccc} -2(0,1)+(0,2)&=&(0,0) \\ \\ -2(1,2)+(2,4)&=&(0,0) \end{array}$

$\begin{array}{ccccc} c_1(a_1,b_1)+c_2(a_2,b_2)=(0,0) &&→&& c_1=c_2=0 \end{array}$

ちょっとややこしいですが

$\begin{array}{rcr} (0,1)+(1,0)&=&(1,1) \\ \\ 0(0,1)+0(1,0)&=&0(1,1) \\ \\ c_1(0,1)+c_2(1,0)&=&(c_1,c_2) \end{array}$

$\begin{array}{ccc} c_1≠0 &→& c_1(0,1)+c_2(1,0)≠(0,0) \\ \\ c_2≠0 &→& c_1(0,1)+c_2(1,0)≠(0,0) \end{array}$

こんな感じになります。

線型従属

補足しておくと

$\begin{array}{ccc} -2(0,1)+(0,2)&=&(0,0) \\ \\ -2(1,2)+(2,4)&=&(0,0) \end{array}$

こういう「線型独立じゃない」

「１直線上」に存在するベクトルたちには

$\begin{array}{ccccc} c_i≠0 &∧& \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} \end{array}$

「線型従属」なんて名前が付いています。

（この場合は次元が $n$ に定まらず定義し辛い）

この辺り少しややこしいですが

１つでも「同一直線上にベクトルがある」場合

$\begin{array}{ccc} (0,1),(0,2),(1,0) &&× \\ \\ (0,0,0),(1,0,0) &&× \end{array}$

これは「線型従属」になり

「線型独立」にはなりません。

線形包 Liner Span

「スカラーとベクトルの積」と「その和」

$\begin{array}{ccc} \mathrm{Span} (B) &=& \displaystyle \left\{ \sum_{n=1}^{N} c_nv_n \,\,\middle| \,\, \begin{array}{ccc} c_1,c_2,...,c_N \in I \\ v_1,v_2,...,v_N\in B \end{array} \right\} \end{array}$

「これで表現できる全てのベクトルを集めた集合」のこと

$\begin{array}{lcccc} c_1,c_2,... &\in& I &⊂&R \\ \\ v_1,v_2,...&\in&B&⊂&V \end{array}$

「和の $cv$ の個数は有限個」に限定されますが

「変数に来るベクトルの集合」の中身は無限個でも良いです。

（無限次元でも和は無限個にならない）

初見だと分かり難いですが

$\begin{array}{ccc} c_1v_1+c_2v_2+\cdots+c_Nv_N &\in& \mathrm{Span} (B) \end{array}$

これは「直線」「平面」「空間」などの

「全ての点を集める」操作になります。

（一部の材料から全体を得る操作）

線形包の具体的な感覚

これは平面で考えると分かりやすいです。

$\begin{array}{ccc} R^2 &=& \{ (x,y) \mid x,y\in R \} \end{array}$

例えばこのような平面の中にある

$\begin{array}{lcl} v_x &=& (1,0) &\in& R^2 \\ \\ v_y &=& (0,1) &\in& R^2 \\ \\ v_{y=x} &=& (1,1) &\in& R^2 \end{array}$

このような「点を意味するベクトル」を考えた時

$\begin{array}{lcl} \mathrm{Span}(\{v_x\}) &=& \{ (r,0) \mid r\in R \} && x軸 \\ \\ \mathrm{Span}(\{v_y\}) &=& \{ (0,r) \mid r\in R \} && y軸 \\ \\ \mathrm{Span}(\{v_{y=x}\}) &=& \{ (r,r) \mid r \in R \} && y=xの直線 \\ \\ \mathrm{Span}(\{v_x,v_y\}) &=& \{ (x,y) \mid x,y\in R \} && 平面 \end{array}$

この「線形包」が意味する「点の集まり」は

このような形になります。

線形包はベクトル空間の部分集合になる

「ベクトル空間 $(V,+,\times) \,\,\mathrm{on} \,\, S$ 」が定められた時

$\begin{array}{ccc} v_1,v_2,...,v_n &\in& V \end{array}$

「 $V$ の全てのベクトル」を集めると

（線型従属なベクトルも含む）

$\begin{array}{ccc} v&=&1\cdot v \end{array}$

自身により自身を表現できるのは明らかですから

$\begin{array}{ccc} V &=& \mathrm{Span} (V) \end{array}$

その「線形包」は当然このようになります。

（つまり最大の線形包は $V$ の線形包）

部分集合の線形包

ということであれば

「 $V$ の部分集合 $V_*$ 」の「線形包」は

$\begin{array}{ccc} \mathrm{Span}(V_*) &⊂& V \end{array}$

直感的にはこうなりそうなわけですが

まだこの時点じゃ自明では無いので

$\begin{array}{ccc} v\in \mathrm{Span}(V_*) &\to& v\in V \end{array}$

線形包 $\mathrm{Span}(V_*)$ の要素を

$V$ が全て持つと言い切るためには

そうなることをきちんと証明する必要があります。

部分集合であることの証明

これは定義から整理していくと

「 $V_*$ は $V$ の部分集合である」という前提より

$\begin{array}{ccc} v_1,v_2,...,v_k&\in&V_* &⊂& V \end{array}$

これらが全て $V$ の要素でもあることから

（使えるスカラー $c$ も $V$ のものと同じ）

$\begin{array}{ccc} c_1v_1+c_2v_2+\cdots+c_kv_k &\in& \mathrm{Span}(V_*) \end{array}$

「線形包」の定義より

「 $\mathrm{Span}(V_*)$ の全ての要素」はこうなるので

（このように表現できないベクトルは要素ではない）

$\begin{array}{ccc} cv &\in& V \\ \\ v+u &\in& V \end{array}$

「ベクトル空間の公理」より

$\begin{array}{ccc} c_1v_1+c_2v_2+\cdots+c_kv_k &\in& V \end{array}$

これは明らかにこうなると言えます。

（同様の手順で部分空間であることも確かめられる）

基底 Basis

|| 次元の数を決めるもの

「線型独立」な「 $V$ を生成する集合」のこと

$\begin{array}{ccccc} (0,1),(0,2) &&→&&\mathrm{Line} \\ \\ (0,1),(1,0) &&→&&\mathrm{Area} \end{array}$

$\begin{array}{ccccc} \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} &&→&& c_1=c_2=\cdots=c_n=0 \end{array}$

この時の $n$ が「次元」になります。

$\begin{array}{ccc} \{v_1,v_2,v_3,...,v_n\} \end{array}$

これについては

「標準基底」を見た方が理解しやすいと思います。

標準基底 Standard Basis

例えば「ベクトル」の「標準基底」は

$\begin{array}{ccc} (a,b)&=&a(1,0)+b(0,1) \end{array}$

こうやって分解できることから

$\begin{array}{ccc} \{ & (1,0) \\ \\ & (0,1) & \} \end{array}$

このような形で定義されます。

同様に

３次元の場合

$\begin{array}{ccc} (a,b,c)&=&\displaystyle \begin{array}{crc} & a(1,0,0) \\ \\ +&b(0,1,0) \\ \\ +&c(0,0,1) \end{array} \end{array}$

「標準基底」は

$\begin{array}{ccc} \{ & (1,0,0) \\ \\ & (0,1,0) \\ \\ & (0,0,1) & \} \end{array}$

このようになります。

基底と標準基底

「基底」という概念は

この「標準基底」を一般化したもので

「直交（標準基底）」→「向きが違う（基底）」

こんな感じに一般化した結果

$\begin{array}{ccccc} \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} &&→&& c_1=c_2=\cdots=c_n=0 \end{array}$

「線型独立」での定義になっています。

（ $V$ を生成するという条件はそのまま）

正規直交基底

補足しておくと

これに追加する形で

以下の条件を満たすものには

$\begin{array}{ccc} ||v||&=&1 \end{array}$

$\begin{array}{ccc} i≠j &→&v_i \cdot v_j=0 \end{array}$

「正規直交基底」なんて名前が付いています。

（これの代表例が標準基底・基本ベクトル）

基底の厳密な定義

「基底」という概念は

$\begin{array}{ccc} v_1,v_2,...,v_n&\in&V \end{array}$

「ベクトル空間 $V$ 」に定義されるもので

$\begin{array}{ccc} B&⊂&V \end{array}$

いくつかの条件を満たす

「 $V$ の部分集合 $B$ 」として定義されています。

「基底」であるために必要な条件は主に２つ

$\begin{array}{ccccc} \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} &&→&& c_1=c_2=\cdots=c_n=0 \end{array}$

１つが「部分集合 $B$ が線型独立である」こと

そしてもう１つが

$\begin{array}{ccc} c_1 v_1+c_2 v_2+\cdots + c_n v_n &=&v&\in&V \end{array}$

「 $V$ の全ての要素を線形結合で表せる」ことで

基本的にこの２つの条件さえ満たしていれば

その「 $V$ の部分集合」は「基底」だと言えます。

ちなみに

「 $V$ が有限次元ベクトル空間」の場合には

$\begin{array}{ccc} |B|&<&\infty \end{array}$

「要素数が有限個である」という条件も付くことがあります。

（これは有限次元の定義により導くことが可能）

まとめると

$\begin{array}{ccc} c_1 v_1+c_2 v_2+\cdots + c_n v_n &=&v \end{array}$

「ベクトル空間の全ての要素 $v$ 」を表現できる

$\begin{array}{ccccc} \displaystyle\sum_{k=1}^{n}c_kv_k=\vec{0} &&→&& c_1=c_2=\cdots=c_n=0 \end{array}$

「線型独立」な「 $V$ の部分集合」

$\begin{array}{ccc} \{ v_1,v_2,v_3,...,v_n \} \end{array}$

これが「基底」の厳密な定義になります。

（線形包の定義に類似しているが別物）

基底の線形包

以上のことから

$\begin{array}{lcl} \mathrm{Span}(\{(1,0)\}) &=& \{ (x,0) \mid x\in R \} && x軸 \\ \\ \mathrm{Span}(\{(0,1)\}) &=& \{ (0,y) \mid y\in R \} && y軸 \\ \\ \mathrm{Span}(\{(1,0),(0,1)\}) &=& \{ (x,y) \mid x,y\in R^2 \} && 平面 \end{array}$

「標準基底」を見れば分かるように

$\begin{array}{lcl} \mathrm{Span}\left(\left\{ \begin{array}{ccc} (1,0) \\ (0,1) \end{array} \right\}\right) &=& \{ (x,y) \mid x,y\in R \} && 平面 \\ \\ \mathrm{Span}\left(\left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \\ (0,0,1) \end{array} \right\}\right) &=& \{ (x,y,z) \mid x,y,z\in R \} && 空間 \end{array}$

「基底」の「線形包」は

「ベクトルの個数」と等しい「次元」を持つ

そんな「空間全体の点集合」になることが分かります。

基底は定数と和で標準基底に変換可能

明らかな結論じゃないので詳細は省きますが

（有限次元では成立するが無限次元だと怪しい）

$\begin{array}{ccc} 標準基底で表現可能なベクトル && 任意の基底 \\ \\ c_1(1,0)+c_2(0,1) &=& (a_1,b_1)+(a_2,b_2) \end{array}$

「任意の基底」は「標準基底」で表現できるので

$\begin{array}{lcc} c_1 &=& a_1+a_2 \\ \\ c_2 &=& b_1+b_2 \end{array}$

「基底」は「標準基底」に変換して

$\begin{array}{ccc} c_1 &=& \displaystyle \sum_{n=1}^{N} c_{1n} \\ \\ c_2 &=& \displaystyle \sum_{n=1}^{N} c_{2n} \\ \\ &\vdots \\ \\ c_N &=& \displaystyle \sum_{n=1}^{N} c_{Nn} \end{array}$

直感的には特に問題無いと言えます。

（この時点ではイメージの補強だと思ってください）

線形結合と連立方程式

線形結合の形から分かるように

$\begin{array}{ccc} v&=&c_1v_1+c_2v_2+c_3v_3 \end{array}$

例えば $3$ 次元なら

$\begin{array}{ccc} \begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} &=& \displaystyle c_1 \begin{pmatrix} v_{11} \\ v_{12} \\ v_{13} \end{pmatrix} + c_2 \begin{pmatrix} v_{21} \\ v_{22} \\ v_{23} \end{pmatrix} + c_3 \begin{pmatrix} v_{31} \\ v_{32} \\ v_{33} \end{pmatrix} \end{array}$

「 $3$ 元一次連立方程式」を使えば

$\begin{array}{ccc} \left\{ \begin{array}{lcl} c_1v_{11} + c_2v_{21} + c_3v_{31} &=& e_1 \\ c_1v_{12} + c_2v_{22} + c_3v_{32} &=& e_2 \\ c_1v_{13} + c_2v_{23} + c_3v_{33} &=& e_3 \end{array} \right. \end{array}$

「任意のベクトル」に対応する

「スカラー定数」を求めることができます。

（ $v$ と $v_n$ の中身が分かってるとする）

そしてこれは

$\begin{array}{ccc} \begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} &=& \displaystyle c^*_1 \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + c^*_2 \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + c^*_3 \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{array}$

結局こういう形に落ち着くので

「標準基底」の話になるんですが

これが必ず標準基底に変換できる保証は

この時点では「連立方程式の解き方」しかないので

$\begin{array}{lcc} c_1 &=& \displaystyle \frac{e_{1}( v_{22}v_{33} - v_{32}v_{23})+v_{21}(e_{2}v_{33} - v_{32}e_{3}) + v_{31} (e_{2}v_{33} - v_{32}e_{3})}{v_{11}( v_{22}v_{33} - v_{32}v_{23})+v_{21}(v_{12}v_{33} - v_{32}v_{13}) + v_{31} (v_{12}v_{23} - v_{22}v_{13})} \\ \\ c_2 &=& \displaystyle \frac{v_{11}( e_{2}v_{33} - v_{32}e_{3})+e_{1}(v_{12}v_{33} - v_{32}v_{13}) + v_{31} (v_{12}e_{3} - e_{2}v_{13})}{v_{11}( v_{22}v_{33} - v_{32}v_{23})+v_{21}(v_{12}v_{33} - v_{32}v_{13}) + v_{31} (v_{12}v_{23} - v_{22}v_{13})} \\ \\ c_3 &=& \displaystyle \frac{v_{11}( v_{22}e_{3} - e_{2}v_{23})+v_{21}(v_{12}e_{3} - e_{2}v_{13}) + e_{1} (v_{12}v_{23} - v_{22}v_{13})}{v_{11}( v_{22}v_{33} - v_{32}v_{23})+v_{21}(v_{12}v_{33} - v_{32}v_{13}) + v_{31} (v_{12}v_{23} - v_{22}v_{13})} \end{array}$

証明の形はぐっちゃぐちゃになります。

（これでも $\mathrm{det}≠0$ のパターンなので全部ではない）

これを見てわかる通り

「連立方程式」についてはちょっと長くなるので

これの詳細は別の記事で扱うことにします。

基底の存在定理

「全てのベクトル空間」には

「必ず基底が存在する」

$\begin{array}{ccc} V &=& \mathrm{Span} (\{ v_1,v_2,...,v_n \}) \end{array}$

これが「存在定理」の主張で

（基底は線形独立で $V$ の中身を全て表現可能）

$\begin{array}{ccc} c_1 v_1+c_2 v_2+\cdots + c_n v_n &=&v \end{array}$

これが正しいから

「ベクトル空間の存在」を保証すれば

それと同時に「基底の存在」もまた保証されます。

前提の確認

これを証明するにあたり必要になる

$\begin{array}{cccccc} \displaystyle v,u,w&∈&V &&V \,\, \mathrm{is} \,\, \mathrm{Set \,\, of \,\, Vector} \\ \\ a,b&∈&S &&S \,\, \mathrm{is} \,\, \mathrm{Scalar \,\, Field} \end{array}$

$\begin{array}{l} \displaystyle (V,+,\times) \,\, \mathrm{is} \,\, \mathrm{Vector \,\, Space} \,\, \mathrm{on} \,\, S \end{array}$

「ベクトル空間 $(V,+,\times)$ 」について

まずざっと確認しておくと

この存在が保証される場合

$\begin{array}{cccccc} \displaystyle v,u,w&∈&V &&V \,\, \mathrm{is} \,\, \mathrm{Set \,\, of \,\, Vector} \\ \\ a,b&∈&S &&S \,\, \mathrm{is} \,\, \mathrm{Scalar \,\, Field} \end{array}$

まず「スカラー」と「ベクトル」の存在が保証されます。

（ $V,S$ に含まれる数の個数はなんでもいい）

より具体的には

$\begin{array}{ccc} \vec{0},v_1,v_2,...,v_n &\in& V \\ \\ 0,1,c &\in& S \end{array}$

この中にある「全ての要素」の存在が保証されるので

（ $V$ の中身はだいたい無限個のベクトル）

この事実を表す表現として

$\begin{array}{ccc} V &=& \mathrm{Span} (\{ v_1,v_2,...,v_n \}) \end{array}$

「有限個のベクトルで表現可能」という形で

「有限次元」の $V$ は定義されています。

（この時点で基底に対する言及は特に無い）

ベクトル空間と例外

まず最も小さな話として

$\begin{array}{ccc} V&=&\{ \vec{0} \} \end{array}$

「 $0$ 次元」の場合は

（ベクトル空間はこれ以上小さく成り得ない）

$\begin{array}{ccc} \mathrm{Span}(\{\}) &=& \{ \vec{0} \} \end{array}$

「基底」を「空集合」と解釈し

「線形独立である」と定義することで例外とします。

（これは１点の話であり線型従属の定義も満たす）

これはベクトル $v_*$ を１つ考えた時

$\begin{array}{ccc} \mathrm{Span}(\{ v_* \}) &\to& 直線 \end{array}$

基礎になる部分であるにもかかわらず

同様の生成手順では解釈し辛いからで

それ以上の意味は特にありません。

有限次元ベクトル空間では

以上が前提となることから

$\begin{array}{ccc} \vec{0},v_1,v_2,...,v_n &\in& V \\ \\ 0,1,c &\in& S \end{array}$

まずこの存在が保証されて

（任意の有限次元ベクトル空間が存在するため）

この存在により

$\begin{array}{ccc} v_0 &=& \vec{0} \end{array}$

このパターン以外もまた保証されます。

（ $V=\{ \vec{0} \}$ の場合は分かっている）

ちなみに「有限次元ベクトル」というのは

$\begin{array}{lcl} v_{\mathrm{Area}} &=& (x,y) \\ \\ v_{\mathrm{Space}} &=& (x,y,z) \\ \\ v_{\mathrm{limited}} &=& (x_1,x_2,...,x_n) \end{array}$

具体的にはこういうやつです。

これに対し

$\begin{array}{ccc} v_{\mathrm{unlimited}} &=& (x_1,x_2,...,x_n,x_{n+1},...) \end{array}$

「無限次元ベクトル」はこんな感じになります。

（こちらは構成法が特殊なので後回し）

直線では

$V$ はベクトルを持ち

$V≠\{ \vec{0} \}$ であるとすると

$\begin{array}{ccc} v_1&≠& \vec{0} \end{array}$

ベクトル空間の存在を保証すれば

$\begin{array}{ccc} v_1 &\in & V \end{array}$

まずこうなることは明らかだと言えます。

（この時点で $V$ は $-v_1$ と $cv_1$ を持つ）

とすると

$\begin{array}{ccc} cv_1 = \vec{0} &&\to&& c=0 \end{array}$

$\{v_1\}$ は明らかに「線形独立」ですから

（ $0$ ベクトルでは無いので）

$\begin{array}{ccc} \{v_1\} &\mathrm{is}& \mathrm{Basis} \end{array}$

これは $V$ が直線の場合に限れば

明らかに「基底」の定義を満たすと言えます。

（線形結合の定義については $cv_1$ の形より明らかとする）

平面や空間なら

$V$ が「直線」であれば

↑ の時点で定理は示されたと言えますが

$\begin{array}{lcl} V_{\mathrm{Line}} &=& \mathrm{Span} (\{ (1,0) \}) \\ \\ V_{\mathrm{Area}} &=& \mathrm{Span} (\{ (1,0),(0,1) \}) \\ \\ V &=& \mathrm{Span} (\{ v_1,v_2,...,v_n \}) \end{array}$

「平面」や「空間」の点になると

$\begin{array}{lcl} V_{\mathrm{Line}} &=& \mathrm{Span} (\{ (1,1) \}) \\ \\ V_{\mathrm{Line}} &=& \mathrm{Span} (\{ (1,1),(2,2) \}) \\ \\ V_{\mathrm{Area}} &=& \mathrm{Span} (\{ (1,1) ,(0,1) \}) \end{array}$

１つのベクトルでは

全て表現できるとは限らないため

（直線に無い点を平面から見つければこれは明らか）

$\begin{array}{lcl} V &=& \mathrm{Span} (\{ v_1,v_2\}) \\ \\ &≠& \mathrm{Span} (\{ v_1\}) && v_2≠cv_1 \end{array}$

「１つの線形独立なベクトルが必ず基底になる」

これは保証された事実だとは言えません。

「直線」以外の「基底」を得るためには

$\begin{array}{ccc} V &=& \mathrm{Span} (\{ v_1,v_2,...,v_n \}) \end{array}$

必ずこれを満たす必要があって

そのためには「複数のベクトル」が必要になります。

線形包とそれ以外のベクトルの存在

↑ を厳密に説明するために

まず事実確認をしておくと

$\begin{array}{ccc} v&=&c_1v_1+c_2v_2+\cdots+c_nv_n \end{array}$

例えば「 $V$ の中にある全てのベクトル」を使えば

（平面なら平面上の全ての点）

$\begin{array}{ccc} V&=&\mathrm{Span} (V) \end{array}$

「 $V$ の要素を全て得られる」というのは明らかです。

（全てのベクトルは自身 $v=1\cdot v$ で表現できる）

ということは

「 $V$ の部分集合」を適当に選んだ時

$\begin{array}{ccc} V&=&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

「全て線形独立」とは限らない

「基底」を含むこの形ではなく

（これと ↓ で全てのパターンをカバーできる）

$\begin{array}{ccc} V&≠&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

このようになるとした場合

（少なくとも全てのベクトルではない）

$\begin{array}{ccc} V\setminus\mathrm{Span} (\{ v_1,v_2,...,v_k \})&≠&∅ \end{array}$

これは確実にこうなると言えます。

（線型従属ではないベクトルの存在が直感的に明らか）

というのも

$\begin{array}{ccc} V&≠&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

これを前提として

$\begin{array}{ccc} V\setminus\mathrm{Span} (\{ v_1,v_2,...,v_k \})&\textcolor{pink}{=}&∅ \end{array}$

これが「空集合である」と仮定した場合

（不足しているベクトルが無い）

$\begin{array}{ccc} V&⊂&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

$V$ と $\mathrm{Span} (\{ v_1,v_2,...,v_k \})$ の関係は

このようになると言えるので

$\begin{array}{ccc} \{ v_1,v_2,...,v_k \}&⊂&V \\ \\ \mathrm{Span}(\{ v_1,v_2,...,v_k \})&⊂&V \end{array}$

「線形包」は $V$ の部分集合であることから

（ ↑ で確認したように線形包の定義より明らか）

$\begin{array}{ccc} V&=&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

結果、この２つの集合の関係はこうなります。

（お互いがお互いの部分集合なので）

以上より

$\begin{array}{ccc} V&≠&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

これを前提とすると

$\begin{array}{ccc} V\setminus\mathrm{Span} (\{ v_1,v_2,...,v_k \})&\textcolor{pink}{=}&∅ \end{array}$

この仮定から矛盾が得られるので

以下のような「線形包」からは

$\begin{array}{ccc} V&≠&\mathrm{Span} (\{ v_1,v_2,...,v_k \}) \end{array}$

これを補う要素として

$\begin{array}{ccc} V\setminus\mathrm{Span} (\{ v_1,v_2,...,v_k \})&≠&∅ \end{array}$

「不足しているベクトルの存在」を導くことができます。

（これが線形独立かどうかはこの時点ではまだ不明）

線形独立なベクトルを選べる

まず確認しておくと

$\begin{array}{ccc} V&=&\mathrm{Span} \left( \left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \\ (0,0,1) \end{array} \right\} \right) \end{array}$

私たちの直感は

「線形独立であるベクトル」を選択し

$\begin{array}{ccc} \mathrm{Basis}_{D=3} &=& \left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \\ (0,0,1) \end{array} \right\} \end{array}$

「基底」を容易に構築できます。

（標準基底を考えると明らか）

しかしよくよく考えてみると

この具体的な方法は不明瞭です。

$\begin{array}{ccc} \{(1,0,0)\} \end{array}$

まずここから始まることは分かって

（これが線形独立になるのは確認済み）

$\begin{array}{ccc} \left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \end{array} \right\} \end{array}$

次にこれを選ぶという結果は分かるんですが

$\begin{array}{ccc} \{(1,0,0)\} &&\to&& \left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \end{array} \right\} \end{array}$

特にこの辺り

自分が何をしてるのかうまく説明できません。

（どうやってか線形独立なベクトルを選んでる）

線型従属とそれ以外

事実確認をしておくと

$\begin{array}{ccc} r(1,0,0) &≠& (0,1,0) \end{array}$

これが定数倍で表現できないから

$\begin{array}{ccc} c_1(1,0,0)+c_2(0,1,0)=\vec{0} \\ \\ ↓ \\ \\ c_1=c_2=0 \end{array}$

これが「線形独立になる」というのは

ベクトルの選出理由としては非常に分かり易いです。

これを無意識に確認した上で

$\begin{array}{ccc} r(1,0,0) ≠ (0,1,0) &&\to&& \left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \end{array} \right\} \end{array}$

これを選んだというのは

本当にそうかはさておき

しっくりくるプロセスだと言えます。

線形従属と線形包

実際、ベクトルを選ぶ際には

$\begin{array}{l} V \setminus \{ (x,0,0) \mid x\in R \} \\ \\ V \setminus \mathrm{Span}(\{ (1,0,0) \}) \end{array}$

「線型従属なベクトル」を

「全体 $V$ から全て除外」した上で

$\begin{array}{ccl} (0,1,0) &\in& V \setminus \mathrm{Span}(\{ (1,0,0) \}) \\ \\ (0,0,1) &\in& V \setminus \mathrm{Span}(\{ (1,0,0),(0,1,0) \}) \end{array}$

その中から選んでいるため

（空間以降は線型従属じゃなく線形包）

$\begin{array}{lcl} v_2&\in&V\setminus \mathrm{Span}(\{ v_1 \}) \\ \\ v_3&\in&V\setminus \mathrm{Span}(\{ v_1,v_2 \}) \end{array}$

ベクトルの選び方として

この手順は有効な方法の１つだと言えます。

線形独立になるはず

↑ の仮説を確認するために

以下の手順でベクトルを追加してみると

（ベクトルが１つなら線形独立であることは確認済み）

$\begin{array}{ccc} v_2&\in&V\setminus \mathrm{Span}(\{ v_1 \}) \end{array}$

↓ の「ベクトルの集合」は

$\begin{array}{ccc} \{ v_1,v_2 \} &⊂& V \end{array}$

結論から言ってしまうと

間違いなく「線形独立」になります。

というのも

これが「線形独立ではない」と仮定した場合

$\begin{array}{lcc} c_1v_1 &=& v_2 \\ \\ c_1v_1+c_2v_2 &=& \vec{0} \end{array}$

これは「線形従属である」ということになりますから

（これは仮定を前提とした事実）

$\begin{array}{ccc} c_1≠0 &\mathrm{or}& c_2≠0 \end{array}$

まずどちらかの係数 $c$ が $0$ ではないと分かるので

$c_2$ を場合分けして計算してみると

$\begin{array}{ccr} \displaystyle v_2 &=& \displaystyle \frac{-c_1}{c_2}v_1 && c_2≠0 \\ \\ \vec{0} &=& \displaystyle c_1v_1 && c_2=0 && 線形独立 \end{array}$

$c_2$ が $0$ ではないことが分かります。

（これは線形従属という仮定の元での結果）

となると

$\begin{array}{ccc} v_2 &=& \displaystyle \frac{-c_1}{c_2}v_1 && c_2≠0 \end{array}$

これはこうなるはずなんですが

$\begin{array}{ccc} \displaystyle \frac{-c_1}{c_2}v_1 &\in& \mathrm{Span}(\{v_1\}) \end{array}$

これは「線形包」に含まれる要素なので

（線形包の定義より $v_1$ の定数倍を含む）

$\begin{array}{ccc} v_2&\in&V\setminus \mathrm{Span}(\{ v_1 \}) \end{array}$

この前提に矛盾してしまいます。

まとめると

$\begin{array}{ccc} c_1v_1+c_2v_2 &=& \vec{0} \end{array}$

「線型従属である」という仮定の元では

$c_1,c_2$ のどちらかは $0$ ではないことから

$\begin{array}{ccc} c_2=0 && c_1v_1=\vec{0} && 線型独立 \\ \\ c_2≠0 && \displaystyle v_2=\frac{-c_1}{c_2}v_1 && v_2 \in \mathrm{Span}(\{v_1\}) \end{array}$

「 $c_2$ は存在しない」と言えるので

「線型従属である」が誤りであることが分かり

（線型従属となる $c_2$ が存在しない）

この事実から

$\begin{array}{ccc} v_2&\in&V\setminus \mathrm{Span}(\{ v_1 \}) \end{array}$

これを前提とすると

$\{ v_1,v_2 \}$

これが「線形独立になる」という結論が得られます。

（ $c_2=0$ はとれるが線型従属ではない）

空間やそれ以上でも同様

$\{ v_1,v_2 \}$ を「線形独立にできる」ことは分かったので

$\begin{array}{ccc} c_1v_1+c_2v_2 = \vec{0} \\ \\ ↓ \\ \\ c_1=c_2=0 \end{array}$

$\{ v_1,v_2 \}$ を「線形独立」とした上で

$\begin{array}{ccc} v_3 &\in& V\setminus \mathrm{Span}(\{ v_1,v_2 \}) \end{array}$

今度はこれを前提にしてみると

さっきと同様の手順で計算したら

$\begin{array}{ccc} c_3=0 && c_1v_1+c_2v_2=\vec{0} && 線型独立 \\ \\ c_3≠0 && \displaystyle v_3=\frac{-c_1}{c_3}v_1+\frac{-c_2}{c_3}v_2 && v_3 \in \mathrm{Span}(\{v_1\}) \end{array}$

こうなるため

前提として

$\begin{array}{ccc} v_3 &\in& V\setminus \mathrm{Span}(\{ v_1,v_2 \}) \end{array}$

このようにとると

$\{ v_1,v_2,v_3 \}$

これもまた「線形独立」になると言えます。

（同様の手順でいくらでも大きくできる）

線形包と線形独立

以上より

「線形包」と「線形独立」の振る舞いから

$\begin{array}{ccc} v_{n+1}&\in&V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

この形での追加なら

（線形独立な $\{ v_1,v_2,...,v_n \}$ に対して）

$\{ v_1,v_2,...,v_n,v_{n+1} \}$

これが「線形独立になる」ことはほぼ確実なので

↓ が「線形独立」だと仮定した上で

（数学的帰納法の合っていて欲しい仮説）

$\begin{array}{ccc} \{ v_1,v_2,...,v_n \} \end{array}$

これを示すために

$\begin{array}{ccc} \{ v_1,v_2,...,v_n,v_{n+1} \} \end{array}$

これが「線形独立にならない」と仮定してみると

（こっちは合っていて欲しくない仮定）

平面や空間の話と同様の手順を経れば

$\begin{array}{ccc} c_{n+1}=0 && c_1v_1+\cdots+c_nv_n=\vec{0} && 線型独立 \\ \\ c_{n+1}≠0 && \displaystyle v_{n+1}=\frac{-c_1}{c_{n+1}}v_1+\cdots+\frac{-c_n}{c_{n+1}}v_n && v_{n+1} \in \mathrm{Span}(\{v_1,...,v_n\}) \end{array}$

この結果が得られますから

明らかに「線型従属ではない」

ということは

$\{ v_1,v_2,...,v_n \}$

これが「線形独立」であり

$\begin{array}{ccc} v_{n+1}&\in&V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

こうなるとすると

$\{ v_1,v_2,...,v_n,v_{n+1} \}$

これは「線形独立である」と言えます。

（これにより数学的帰納法の要件が満たされる）

有限次元ベクトル空間の定義と操作の回数

感覚的にも分かる通り

$\begin{array}{ccc} v_{n+1}&\in&V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

この一連の操作には

$\begin{array}{ccc} V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_N \}) &=& ∅ \end{array}$

「いつか」終わりが来ます。

「有限」である以上これは直感的に明らかです。

（終わらないと線形独立な無限個の集合ができてしまう）

しかし

これがどのような定義により保証されているのか

$\begin{array}{ccc} V &=& \mathrm{Span}(\{ v_1,v_2,...,v_N \}) \end{array}$

この時点では曖昧ですよね。

（あくまで直感的に明らかな結論）

結論としては

「 $V$ の任意の線形独立な部分集合」に対し

$\begin{array}{ccc} \Bigl| \{ v_1,v_2,...,v_N \} \Bigr| &<& \infty \end{array}$

「その要素数は有限個である」

という定義がこれを保証するんですが

これは知らないと納得できない部分だと思います。

実際、これを知らない状態だと

$\begin{array}{ccc} \{ v_1,v_2,...,v_n,v_{n+1},... \} \end{array}$

「無限回の操作」を許す

そんな仮定によって発生するこの集合が

$\begin{array}{ccc} \Bigl| \{ v_1,v_2,...,v_n,v_{n+1},... \} \Bigr| &=& \infty \end{array}$

「定義に矛盾する」という結論を導くことができません。

（有限回で操作が終わらなければ定義に矛盾する）

有限次元の同値な定義

「線形独立な部分集合の要素数は有限」

これは「有限次元ベクトル空間」の定義なんですが

$\begin{array}{ccc} \Bigl| \{ v_1,v_2,...,v_N \} \Bigr| &<& \infty \end{array}$

「有限次元ベクトル空間」の定義としては

$\begin{array}{ccc} R^3 &=& \displaystyle \mathrm{Span}\left(\left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \\ (0,0,1) \end{array} \right\}\right) \end{array}$

「 $V$ を生成できる有限集合が存在する」

こちらの定義の方がしっくり来ると思います。

（中身が有限個の基底が存在するって話なので）

結論としては

この２つの命題は同値なので

どちらかを定義とすればもう片方も正しくなるんですが

$\begin{array}{ccc} V=\mathrm{Span}(B) \\ \\ |B|<\infty \end{array}$

感覚的にはちょっと遠い感じがするので

同値であることを念のため確認しておこうと思います。

それぞれの定義と論理式

簡単に確認しておくと

まず「有限個のベクトルで表現できる」

$\begin{array}{ccc} \exists V_* ⊂ V & \Bigl( V_* \,\, \mathrm{is} \,\, \mathrm{Finite} \Bigr) ∧ \Bigl( V=\mathrm{Span}(V_*) \Bigr) \end{array}$

$\begin{array}{lcc} V_* \,\, \mathrm{is} \,\, \mathrm{Finite} && \equiv && \exists n\in N \,\, \mathrm{Cardinal}(V_*)=n \end{array}$

これの論理式はこんな感じになっています。

（存在が宣言されてるので有限値 $n$ が使える）

「線形独立な部分集合」は

「全て有限集合である」

$\begin{array}{ccc} \forall V_*⊂V & \left( \Bigl( V_* \,\, \mathrm{is} \,\, \mathrm{Independent} \Bigr) ⇒ \Bigl( V_* \,\, \mathrm{is} \,\, \mathrm{Finite} \Bigr) \right) \end{array}$

こちらの方はこんな感じ。

（自然数の部分集合に上限があれば最大元が存在する）

$\begin{array}{ccc} v_1,v_2,...,v_n &\in& V_* \\ \\ c_1,c_2,...,c_n &\in & R_* \end{array}$

$\begin{array}{ccc} V_* \,\, \mathrm{is} \,\, \mathrm{Independent} \\ \\ \displaystyle \forall c_1,...,c_n \,\, \left( \Bigl( c_1v_1+\cdots+c_nv_n=\vec{0} \Bigr) ⇒\Bigl( c_1=0 ∧ \cdots ∧ c_n=0 \Bigr) \right) \end{array}$

「線形独立」については少し複雑ですが

（ $V_*$ の中身のベクトルは固定されてます）

$\begin{array}{ccc} V_* \,\, \mathrm{is} \,\, \mathrm{Finite} \end{array}$

これは感覚的に明らかなので

特にひっかかる部分は無いと思います。

存在 ⇒ 有限

まず以下の集合 $V_*$ の存在を前提として

（有限個のベクトルで $V$ を生成できる）

$\begin{array}{ccc} V&=&\mathrm{Span}(V_*) \end{array}$

「線形独立な部分集合の要素数は有限である」

これを示してみます。

やることはいつものように「背理法」です。

（無限個のベクトルが線形独立になるはずがない）

$\begin{array}{ccc} \{u_1,u_2,u_3,...,u_k,u_{k+1},...\} \end{array}$

「線形独立な無限集合が存在する」と仮定して

これが前提に矛盾することを示します。

手順は少し複雑です。

$\begin{array}{ccc} V&=&\mathrm{Span}(V_*) \end{array}$

まず事実確認からしておくと

「有限個のベクトルで表現できる」ということは

$\begin{array}{ccc} V_*&=& \{ v_1,v_2,v_3,...,v_N\} \end{array}$

「仮定された有限個のベクトルの個数」が

「有限値 $N$ として存在する」ということで

（最大元の存在については長くなるので別記事で）

それだけではなく

$\begin{array}{ccc} u &=& c_1v_1+c_2v_2+c_3v_3+\cdots+c_Nv_N \end{array}$

「 $V$ 内の任意のベクトル」は

全て線形結合により表現できるということでもあります。

（ $N$ 個のベクトルの有限和で）

ここから

$\begin{array}{ccc} u &=& c_1v_1+c_2v_2+c_3v_3+\cdots+c_Nv_N \end{array}$

「線形結合」を用いれば

$\begin{array}{ccc} \{u_1,u_2,u_3,...,u_k,u_{k+1},...\} \end{array}$

この無限集合と $V$ の対応はとれそうであることから

（無限個のベクトルは線形独立になり得るのか考えられる）

とりあえず

$\begin{array}{ccc} u_1 &=& c_1v_1+c_2v_2+c_3v_3+\cdots+c_Nv_N \end{array}$

まずはこのような形を考えてみます。

（ここまでは事実から自然に分かること）

基底の要素数と無限集合

直感的な話として

$\begin{array}{ccc} R^3 &=& \displaystyle \mathrm{Span}\left(\left\{ \begin{array}{ccc} (1,0,0) \\ (0,1,0) \\ (0,0,1) \end{array} \right\}\right) \end{array}$

例えば「 $3$ 次元」なら

「 $3$ つ以上のベクトル」を用意してみると

$\begin{array}{ccc} (a,b,c)&=& \begin{array}{crc} & a(1,0,0) \\ \\ + & b(0,1,0) \\ \\ + & c(0,0,1) \end{array} \end{array}$

このようになることから

他の全てのベクトルは「線型従属」になると言えます。

（差が $\vec{0}$ になる時に $a,b,c$ が $0$ である必要が無い）

この事実を踏まえると

$\begin{array}{ccc} V_*&=& \{ v_1,v_2,v_3,...,v_N\} \end{array}$

「 $N$ 個のベクトルで全て表現可能」なら

（基底はそれ以下の有限個になるはず）

$\begin{array}{ccc} \{u_1,u_2,u_3,...,u_N,u_{N+1},...\} \end{array}$

「線形独立」な「 $N+1$ 個目のベクトル」は

「線型従属になる」と予想できるため

「無限集合が $V$ を生成する」なら

（これはまだ可能かどうか不明）

$\begin{array}{ccc} V&=& \mathrm{Span}(\{u_1,u_2,u_3,...,u_N,u_{N+1},...\}) &&？ \end{array}$

これは「線型従属」になるはずですから

（直感的には明らかな予想）

そうなれば

$\begin{array}{ccc} \{u_1,u_2,u_3,...,u_N,u_{N+1},...\} \end{array}$

この「無限集合が線形独立である」という仮定は

結果的に矛盾することになります。

$V$ を生成するとしたまま無限集合へ

以上のことから

$\begin{array}{ccc} V&=& \mathrm{Span}(\{u_1,u_2,u_3,...,u_N,u_{N+1},...\}) \end{array}$

これさえ得ることが出来れば

仮定が矛盾すると示せるので

$\begin{array}{lcl} V&=&\mathrm{Span}(V_*) \\ \\ V&=&\mathrm{Span}(\{ v_1,v_2,v_3,...,v_N\}) \end{array}$

定義である前提と

$\{u_1,u_2,u_3,...,u_N,u_{N+1},...\}$

これが「線形独立である」という「仮定」を利用して

（この仮定は間違っていて欲しい仮定）

$\begin{array}{ccc} v_1 & v_2 &\cdots & v_N \\ \\ ↓ & ↓ & {} & ↓ \\ \\ u_1 &u_2&\cdots & u_N \end{array}$

とりあえずこのような形を目指してみます。

（ $V_*$ が $V$ を生成できることから）

具体的な方法としては

$\begin{array}{ccc} (0,0,0)&=& c_0(0,0,0)+c_1(1,0,0)+c_2(0,1,0) \end{array}$

「線形独立である」以上

「ベクトル $u_n$ 」は $\vec{0}$ ベクトルではありませんから

（ $c_0$ がなんであれ $\vec{0}$ になることより）

$\begin{array}{ccc} u_n &=& c_1v_1+c_2v_2+c_3v_3+\cdots+c_Nv_N \end{array}$

いずれかの $c_n$ は $0$ ではないので

$\begin{array}{ccc} \displaystyle \frac{u_n}{c_k} &=& \displaystyle \frac{c_1v_1}{c_k}+\frac{c_2v_2}{c_k}+\cdots+\frac{c_kv_k}{c_k}+\cdots+\frac{c_Nv_N}{c_k} \end{array}$

$0$ ではない $c_k$ を使ってこのようにすれば

$\begin{array}{ccc} v_k &=& \displaystyle \frac{u_n}{c_k} - \left( \frac{c_1v_1}{c_k}+\frac{c_2v_2}{c_k}+\cdots+\frac{c_Nv_N}{c_k} \right) \end{array}$

$v_k$ は他の $v_i$ と $u_n$ で表現可能である。

この事実を利用します。

というのも

以上の関係より

$\begin{array}{ccc} v_k &\in & \mathrm{Span} ( \{ v_1,v_2,...,v_N, u_n \} ) \end{array}$

これは明らかですから

$\begin{array}{lcl} v &=& c_1v_1 + \cdots + c_kv_k +\cdots + c_Nv_N \\ \\ v_k&=& c_1^*v_1+ \cdots +c_k^*u_n+ \cdots + c_N^*v_N \end{array}$

$v_k$ と $u_n$ を入れ替えた集合は

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ v_1,v_2,..., u_n,...,v_N \} ) \end{array}$

「 $V$ を生成できる集合」になると言えるので

（ $v_k$ に $u_n$ が入った線形結合を代入すれば確認できる）

$\begin{array}{ccc} v_1 & v_2 &\cdots & v_N \\ \\ ↓ & ↓ & {} & ↓ \\ \\ u_1 &u_2&\cdots & u_N \end{array}$

後はこれを繰り返すことで

$v_k$ と $u_n$ を入れ替えることができます。

集合の並びに制限は無い

ただ ↑ のままだと

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ v_1,v_2,..., \textcolor{pink}{v_k},...,v_N \} ) \\ \\ V &=& \mathrm{Span} ( \{ v_1,v_2,..., \textcolor{skyblue}{u_n},...,v_N \} ) \end{array}$

どの $v_k$ と $u_n$ が交換されるか分からないので

$\begin{array}{ccc} V&=& \mathrm{Span}(\{u_1,u_2,u_3,...,u_N,u_{N+1},...\}) \end{array}$

この形をうまく作ることができません。

欲しい形に寄せるためには

$\begin{array}{ccc} v_k &\to& u_n \\ \\ v_1 &\to& u_1 \end{array}$

これらの添え字を合わせる必要があります。

これについては

$\begin{array}{ccc} u_1&=& c_1^*v_1+ \cdots +c_k^*v_k+ \cdots + c_N^*v_N && c_k≠0 \\ \\ u_1 &=& c_1v_1 + \cdots + c_kv_k +\cdots + c_Nv_N && c_1≠0 \end{array}$

ちょっと難しい気もしますが

実はよくよく考えてみると単純で

というのも

そもそも順番については

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ v_1,v_2,..., u_n,...,v_N \} ) \end{array}$

少なくともこの前提では特に制限がありません。

$\begin{array}{ccc} (1,0,0) & (0,0,1) & (0,1,0) \\ \\ v^*_1 & v_2^* & v_3^* \\ \\ v_1 & v_3 & v_2 \end{array}$

実際、これは数字の列をそのまま表現してるだけなので

並び替えて添え字を変えても中身は同じです。

なので

$\begin{array}{ccc} \displaystyle \frac{u_1}{c_1} &=& \displaystyle v_1+\frac{c_2}{c_1}v_2+\frac{c_3}{c_1}v_3+\cdots+\frac{c_N}{c_1}v_N \end{array}$

$c_k\neq0$ になる要素を

ただ $1$ 番目に持ってくるだけで

$\begin{array}{ccc} v_1&=& \displaystyle \frac{u_1}{c_1} - \frac{c_2}{c_1}v_2-\frac{c_3}{c_1}v_3-\cdots -\frac{c_N}{c_1}v_N \end{array}$

添え字は揃えることができるので

$\begin{array}{ccc} u_1&=& c_1^*v_1+ \cdots +c_k^*v_k+ \cdots + c_N^*v_N && c_k≠0 \\ \\ u_1 &=& c_1v_1 + \cdots + c_kv_k +\cdots + c_Nv_N && c_1≠0 \end{array}$

特になにをするでもなく

添え字は揃えることができてしまいます。

（やることはただ記号を変更するだけ）

最初だけではない

これは $1$ 番目に限った話ではなく

$\begin{array}{ccc} u_2 &=& c_1u_1 + c_2v_2 +\cdots + c_Nv_N && c_2≠0 \end{array}$

$2$ 番目以降も同様なので

$\begin{array}{ccl} V &=& \mathrm{Span} ( \{ u_1,v_2,...,v_N \} ) \\ \\ V &=& \mathrm{Span} ( \{ u_1,u_2,...,v_N \} ) \end{array}$

同じような手順を辿れば

こんな形の集合もまた作ることができます。

確認しておくと

$\begin{array}{ccc} \{ u_1,u_2,u_3,...,u_n,u_{n+1},... \} \end{array}$

「仮定」より

これは「線形独立」なので

$\begin{array}{ccc} \{ u_1,u_2,u_3,...,u_n \} \end{array}$

この部分集合もまた「線形独立」になります。

（和が $\vec{0}$ になるためには定数が全て $0$ ）

言い換えると

$\begin{array}{lclcl} u_2 &≠& c_1u_1 && c_1≠0 \\ \\ u_3&≠& c_1u_1+c_2u_2 && c_1≠0 ∨c_2≠0 \end{array}$

こうなるということなので

$\begin{array}{ccc} u_2 &=& c_1^*u_1 + c_2^*v_2 +\cdots + c_N^*v_N \end{array}$

この形を考えた時

$\begin{array}{ccc} u_2 &=& c_1^*u_1 \end{array}$

「線形独立」という条件ではこうならない以上

（先述したように $u_2$ は $\vec{0}$ ではない）

$\begin{array}{ccc} c^*_2 &=& \cdots &=& c_N^* &=& 0 \end{array}$

こうはならないので

$\begin{array}{ccc} v_2&=& \displaystyle -\frac{c_1}{c_2}u_1 + \frac{1}{c_2}u_2-\frac{c_3}{c_2}v_3 - \cdots - \frac{c_N}{c_2}v_N \end{array}$

定数 $c_2\neq0$ とできることから

（ $c^*_k\neq0$ となる $k$ が存在する）

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ u_1,u_2,...,v_N \} ) \end{array}$

これもまたこうなると言えます。

これ以上の場合もロジックは同じ。

$\begin{array}{ccc} u_3 &=& c_1^*u_1+c_2^*u_2 \end{array}$

こうならない以上

（線形独立という仮定）

$\begin{array}{ccc} c^*_3 &=& \cdots &=& c_N^* &=& 0 \end{array}$

こうはならないので

（この場合は成立しない形に）

$\begin{array}{ccc} v_3&=& \displaystyle -\frac{c_1}{c_3}u_1 - \frac{c_2}{c_3}u_2 + \frac{1}{c_3}u_3 - \cdots - \frac{c_N}{c_3}v_N \end{array}$

このようにとれると言えることから

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ u_1,u_2,u_3,v_4,...,v_N \} ) \end{array}$

こうなると言えます。

線形独立にできる限界がある

↑ の操作は何回もできるため

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ u_1,u_2,...,u_k,v_{k+1},...,v_N \} ) \end{array}$

「 $u_n$ が無限個存在する」以上

このようになるのは確実であり

$\begin{array}{ccc} \Bigl| \{ v_1,v_2,...,v_N \} \Bigr| &=&N \end{array}$

$V_*$ の要素数が $N$ であることから

（これは定義である前提から分かる事実）

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ u_1,u_2,...,u_N \} ) \end{array}$

$k=N$ の場合では

これが $V$ を生成することも明らかだと言えます。

ということは

$u_{N+1}$ というベクトルを考えた時

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ u_1,u_2,...,u_N \} ) \end{array}$

これで全ての要素を線形結合で表現できることから

$\begin{array}{lcl} u_{N+1} &\in& \mathrm{Span} ( \{ u_1,u_2,...,u_N \} ) \\ \\ u_{N+1} &=& c_1u_1+c_2u_2+\cdots+c_Nu_N \end{array}$

$u_{N+1}$ はこのように表現可能だと言えるので

（この時点で線形独立に反する）

$\begin{array}{ccc} \{ u_1,u_2,...,u_N,u_{N+1} \} \end{array}$

これは「線形独立」になりません。

同様に

$\begin{array}{ccc} u_{N+2} &=& c_1u_1+c_2u_2+\cdots+c_Nu_N \\ \\ u_{N+3} &=& c_1u_1+c_2u_2+\cdots+c_Nu_N \\ \\ &\vdots \end{array}$

$N+1$ 以降の $u_n$ は

全て $V$ の要素ですから

$\begin{array}{ccc} \{ u_1,u_2,u_3,...,u_n,u_{n+1},... \} \end{array}$

この「無限集合が線形独立である」という仮定

$\begin{array}{lcl} u_{N+1} &=& c_1u_1+c_2u_2+\cdots+c_Nu_N \\ \\ u_{N+1} &=& c_1u_1+c_2u_2+\cdots+c_Nu_N + 0( u_{N+2} + \cdots ) \end{array}$

これは部分集合と同様の理屈で

（ $1$ と $N$ の間に $0$ ではない $c_k$ が存在する）

$\begin{array}{lcl} V &=& \mathrm{Span} ( \{ v_1,v_2,...,v_N \} ) \\ \\ V &=& \mathrm{Span} ( \{ u_1,u_2,...,u_N \} ) \end{array}$

前提に矛盾すると言えます。

有限 ⇒ 存在

「線形独立な集合は全て有限」

こちらの方を前提とした時

$\begin{array}{ccc} \Big| \{ v_1,v_2,...,v_n \} \Bigr| &<& \infty \end{array}$

これから「有限集合で $V$ を表現可能」を得るには

$\begin{array}{ccc} \Big| \{ v_1,v_2,...,v_n \} \Bigr| &<& N \end{array}$

「最大の線形独立な集合」を考える必要があります。

（全て有限なら最大値 $N$ もまた有限）

というのも

$\begin{array}{ccc} V &=& \mathrm{Span}(\{ v_1,v_2,...,v_N \}) \end{array}$

$3$ 次元などの具体例を考えると

これが「 $V$ を生成する」と推定できるので

（ $3$ 次元なら $3$ 個で十分なため）

「サイズが最大の線形独立な集合」が

$\begin{array}{ccc} V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_N \}) &≠& ∅ \end{array}$

「 $V$ を生成しない」と仮定すると

まず間違いなく矛盾すると予想ができます。

線形独立なベクトルを選べる

先に確認した通り

$\begin{array}{ccc} v_{N+1} &\in& V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_N \}) \end{array}$

この操作を行えば

「線形独立なベクトル $v_{N+1}$ 」を選び

（これが線形独立ではないとすると矛盾する）

$\begin{array}{ccc} \{ v_1,v_2,...,v_N,v_{N+1} \} \end{array}$

新たに「線形独立な集合」を作ることができます。

（あくまでこのような $v_{N+1}$ が存在するなら）

ということは

$\begin{array}{ccc} \{ v_1,v_2,...,v_N \} \end{array}$

「最大サイズであるはずの線形独立な集合」より

（これは前提から得られる事実）

$\begin{array}{ccc} \{ v_1,v_2,...,v_N,v_{N+1} \} \end{array}$

これは「線形独立」でありながら

「要素数が $N$ より多い集合」になるので

この事実は

$\begin{array}{ccc} \Big| \{ v_1,v_2,...,v_N,v_{N+1} \} \Bigr| &<& N && × \end{array}$

「最大の線形独立な集合」という前提に矛盾します。

結果

「最大の集合は $V$ を生成できない」

この仮定は前提に矛盾することから

$\begin{array}{ccc} V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_N \}) &≠& ∅ \end{array}$

この仮定は誤りであると言えます。

まとめると

「最大の線形独立な集合」を考える場合

$\begin{array}{ccc} V &=& \mathrm{Span}(\{ v_1,v_2,...,v_N \}) \end{array}$

これは必ずこうなります。

（有限個のベクトルで $V$ を表現可能）

有限次元ベクトル空間と基底の存在

以上をまとめると

$\begin{array}{lcl} v_2 &\in& V\setminus \mathrm{Span}(\{ v_1 \}) \\ \\ v_3 &\in& V\setminus \mathrm{Span}(\{ v_1,v_2 \}) \end{array}$

「初期値 $\{v_1\}$ 」から「一定の後者規則」により

$\begin{array}{ccc} v_{n+1}&\in&V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

「線形独立なベクトルの集合」を作れることと

「有限次元ベクトル空間」の中身が

$\begin{array}{ccc} V&=&\mathrm{Span}(\{ v_1,v_2,...,v_N \}) \end{array}$

「無限次元ベクトルではない」ことより

（線形独立な部分集合は全て要素数が有限）

$\begin{array}{ccc} V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_N \}) &=& ∅ \end{array}$

この操作は確実に「有限回で終わる」ことから

（唯一存在定理によりこの回数 $N$ が定まる）

結果として

「有限次元ベクトル空間」には

$\begin{array}{ccc} \{ v_1,v_2,...,v_N \} \end{array}$

「必ず基底が存在する」という結論が導かれます。

（要素数が一定かなどの詳細はまだ不明）

基底の複数存在定理

「 $2,3$ 次元での具体例」や

「基底の存在定理」から直感的には明らかですが

$\begin{array}{ccc} V&=&\mathrm{Span}(\{(1,0),(0,1)\}) \\ \\ V&=&\mathrm{Span}(\{(1,1),(1,2)\}) \end{array}$

「全ての有限次元ベクトル空間」でそうなるか

$\begin{array}{lcl} V &=& \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \\ \\ V &=& \mathrm{Span}(\{ v_1,v_2,...,v_m \}) \end{array}$

これはまだ不明なので

ここで念のために証明しておきます。

例外の処理

実際問題として

$\begin{array}{ccc} V&=&\{ \vec{0} \} \end{array}$

このような「有限次元ベクトル空間」を考えると

これには「複数の基底」が存在しません。

逆元を $-1=1$ とする例など

（ $Z_2$ は二元体という最小の体 $\mathrm{Field}$ ）

$\begin{array}{ccc} 0,1 &\in& Z_2 \\ \\ \vec{0},v &\in&V \end{array}$

極端に小さなベクトル空間に限りますが

「複数の基底が存在する」は非自明です。

複数存在するだろう最小のサイズ

↑ の例外を見るに

$\begin{array}{ccc} -1,0,1 &\in& Z_3 \\ \\ -v,\vec{0},v &\in&V \end{array}$

「基底が複数存在する」と言える前提は

$\begin{array}{ccc} \{-v\} & \{v\} \end{array}$

これが最小だと言えそうですが

（定義上は最小から増やしてるので明らか）

最小かどうかは議論の余地ありで

$\begin{array}{ccc} 0,1 &\in& Z_2 \end{array}$

というのも

例えば「要素数 $2$ の基底」を考えてみると

$\begin{array}{ccc} v_1,v_2 &\in& V \end{array}$

これは「二元体 $Z_2$ 」であっても

$\begin{array}{ccc} \{(1,0),(0,1)\} \\ \\ \{ (1,1),(0,1) \} \end{array}$

「基底が複数存在する」と言えるので

こちらの増やし方も最小であると解釈できます。

基底が１つしかないと仮定する

以上より

$\begin{array}{ccc} B &=& \{v_1,v_2,v_3,...,v_n\} \end{array}$

「基底の存在定理」から

「基底が最低でも１つ存在する」とした上で

$\begin{array}{ccc} \Bigl( |B|=1 ∧ 3≤|F| \Bigr) &∨& 2≤|B| \end{array}$

「要素数 $1$ なら体 $F$ の要素数は $3$ 以上」

または「要素数 $2$ 以上」を前提としてみます。

（直感的にこれ以上だと基底は複数個になるはず）

そうすると

雑に構成してみても

$\begin{array}{ccc} \{ (1,0,0),(0,1,0),(0,0,1) \} \\ \\ \{ (1,1,0),(0,1,0),(0,0,1) \} \end{array}$

単純な和で複数の基底が構成できるので

$\begin{array}{ccc} B &=& B^{\prime} \end{array}$

「基底が１つしかない」と仮定した場合

$\begin{array}{ccc} v_* \not\in B ∧ v_* \in B^{\prime} &→& B ≠ B^{\prime} \end{array}$

これが矛盾を導くことは容易に推測できます。

（異なる要素が１つでも基底の中にあれば良いので）

反例の構成

この証明の核となる「反例」

これは無数に考えられますが

$\begin{array}{ccc} \{ (1,0,0),(0,1,0),(0,0,1) \} \\ \\ \{ (1,1,0),(0,1,0),(0,0,1) \} \end{array}$

この形を考えると

$\begin{array}{ccc} v_* &=& v_1+v_2 \end{array}$

最もシンプルな形として

このような形を推定することができます。

（この時点ではこれが常に反例になるか不明）

ざっと確認してみても

$\begin{array}{ccc} v_1& v_2 & v_3 & v_4 \\ \\ (1,0,0,0) &(0,1,0,0)& (0,0,1,0) & (0,0,0,1) \end{array}$

$v_1,v_2$ は他と「線型従属ではない」ですし

（これは基底の定義から明らかとして良い）

$\begin{array}{ccc} (1,1,0,0) \end{array}$

これも「線型従属ではありません」

それに $v_1,v_2$ であれば

$\begin{array}{ccc} v_1 &=& v_1+v_2 - v_2 \\ \\ (1,0,0,0) &=& (1,1,0,0)- (0,1,0,0) \end{array}$

$v_1+v_2$ ともう片方で表現可能なので

$V$ の生成も問題無くできそうです。

（順番的には具体例の比較の後にこれを確認してる）

反例だと予想される集合の中身

まず確認しておくと

$\begin{array}{ccc} B &=& \{ v_1,v_2,...,v_n \} \end{array}$

この「基底 $B$ 」は「線形独立」です。

（これは基底の定義の１つなので明らか）

ということは

$\begin{array}{ccc} V &=& \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

「 $V$ を生成する」以上

（これも基底の定義の１つなので明らか）

$\begin{array}{ccc} v_1+v_2 &\in & V \end{array}$

各要素の線形結合は

必ずこうなると言えるので

$\begin{array}{ccc} B^{\prime} &=& \{ v_1+v_2,v_2,...,v_n \} \end{array}$

１つの要素を入れ替えた

これもまた「 $V$ の部分集合」になります。

そして $v_1+v_2$ は

$\begin{array}{ccl} v_1+v_2 &=& v_1 && × \\ \\ v_1+v_2 &=& v_2 && × \end{array}$

「線形独立」である以上

明らかに元のベクトルとは異なる上に

（基底の要素は $\vec{0}$ ではない）

$\begin{array}{lccc} v_1+v_2 &=& v_k && × \\ \\ v_1+v_2 - v_k &=& \vec{0} && 線型独立ではない \end{array}$

その他のベクトルとも異なるので

（基底の要素である $v_k$ は $v_1,v_2$ と線形独立）

$\begin{array}{ccc} \forall k \in \{ 1,2,...,n \} & v_k≠v_1+v_2 \end{array}$

「全ての $v_k$ と異なるベクトル」になると言えるため

以上の結果から

「外延性公理」より

$\begin{array}{ccc} \forall e \,\, \Bigl( e\in A ⇔ e\in B \Bigr) &⇒& A=B \end{array}$

「 $B$ は $v_1+v_2$ を持たない」上に

「 $B^{\prime}$ は $v_1$ を持たない」ことから

$\begin{array}{lcl} B &=& \{ v_1,v_2,...,v_n \} \\ \\ B^{\prime} &=& \{ v_1+v_2,v_2,...,v_n \} \end{array}$

集合 $B,B^{\prime}$ は

「同じにならない」ということが分かります。

反例だと予想される集合は基底であるか

「 $V$ の線形独立な部分集合 $B^{\prime}$ 」は

「基底 $B$ とは異なる集合」である

これは分かりましたが

$\begin{array}{ccc} B^{\prime} &=& \{ v_1+v_2,v_2,...,v_n \} \end{array}$

これが「基底であるか」はまだ分かっていません。

（基底になる具体例は標準基底から得られている）

先に確認した通り

$\begin{array}{lccc} v_1+v_2 &=& v_k && × \\ \\ v_1+v_2 - v_k &=& \vec{0} && 線型独立ではない \end{array}$

「線形独立」であることは分かっていますが

（ $B^{\prime}$ の他の要素は $v_1$ 以外 $B$ と同じ）

$\begin{array}{ccc} V &=& \mathrm{Span}(\{ v_1+v_2,v_2,...,v_n \}) && ？ \end{array}$

これが「 $V$ を生成するか」はまだ不明です。

（具体例を見るに直感的には生成しそう）

ただ具体例を参考に

「基底 $B$ 」の定義を確認してみると

$\begin{array}{ccc} v &=& c_1^*v_1+c_2^*v_2+\cdots+ c_n^*v_n \end{array}$

線形結合の形はこうですから

（ $V$ の全ての要素を表現できる）

$\begin{array}{ccc} v_1 &\to& v_1+v_2 \end{array}$

集合の中身がほとんど同じであることを考えると

（線形結合の形はほぼ同じになる）

$\begin{array}{ccc} v_1&=& 1 \cdot (v_1+v_2) + (- 1) \cdot v_2\end{array}$

$v_1$ はこんな形ですし

（ $B^{\prime}$ の要素の線形結合で表現可能）

$\begin{array}{lcl} c_1(v_1+v_2) + c_2v_2+\cdots+ c^*_nv_n \\ \\ c_1v_1 + (c_1+c_2) v_2 + \cdots + c^*_n v_n \end{array}$

このようになると言えるので

$\begin{array}{ccc} c_2&=& c^*_2-c_1 \end{array}$

後はこれをこのように解釈すれば

$\begin{array}{lcc} c_1v_1 + (c_1+c_2) v_2 + \cdots + c^*_n v_n \\ \\ c_1v_1 + (c_1+c_2^* - c_1)v_2 + \cdots + c_n v_n \end{array}$

「 $B^{\prime}$ の線形結合」は

このように「基底 $B$ の線形結合」の形になるので

$\begin{array}{ccc} v&=& c_1(v_1+v_2) + c_2v_2+\cdots+ c^*_nv_n \end{array}$

「 $V$ の部分集合 $B^{\prime}$ 」は

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ v_1+v_2,v_2,...,v_n \} ) \end{array}$

「 $V$ の全ての要素を表現できる」と言えます。

（ $V$ を生成するという条件を満たす）

基底は複数存在する

まとめると

$\begin{array}{lcl} B &=& \{ v_1,v_2,...,v_n \} \\ \\ B^{\prime} &=& \{ v_1+v_2,v_2,...,v_n \} \end{array}$

「基底 $B$ 」と比較して

$\begin{array}{ccc} B &≠& B^{\prime} \end{array}$

「要素が１つだけ異なる $B^{\prime}$ 」を考えた時

（線形独立なので $\forall k \in \{ 1,2,...,n \} \,\, v_k≠v_1+v_2$ ）

この $B^{\prime}$ は「線形独立」になり

$\begin{array}{lccc} v_1+v_2 &=& v_k && × \\ \\ v_1+v_2 - v_k &=& \vec{0} && 線型独立ではない \end{array}$

「基底」の定義から

$\begin{array}{ccl} v&=& c_1(v_1+v_2) + c_2v_2+\cdots+ c^*_nv_n \\ \\ &=& c_1v_1 + (c_1+c_2) v_2 + \cdots + c^*_n v_n \end{array}$

「 $V$ を生成する」ことも明らかなので

$\begin{array}{ccc} V &=& \mathrm{Span} ( \{ v_1+v_2,v_2,...,v_n \} ) \end{array}$

「 $B^{\prime}$ は基底の定義を満たす」ことから

「基底は複数存在する」という結論が得られます。

基底の要素数の唯一性

これは「基底の要素数は全て同じ」という

「基底の要素数」に関することを主張する定理です。

$\begin{array}{ccc} |B_1| &=& |B_2| &=& \cdots \end{array}$

「基底の要素数」が「次元」である

$\begin{array}{ccc} \mathrm{Dim}(V) &=& \mathrm{Cardinal}\Bigl( \mathrm{Basis}(V) \Bigr) \end{array}$

この定理はこれを厳密に保証してくれます。

（これにより次元という概念がきちんと定まる）

基底の存在と要素数

「基底の存在定理」より

$\begin{array}{lcl} B_1 &=& \{ v_1,v_2,...,v_n \} \\ \\ B_2 &=& \{ u_1,u_2,...,u_m \} \end{array}$

$V$ には必ず「基底が存在する」わけですが

$\begin{array}{ccc} |B_1|&<&|B_2| && ？ \\ \\ |B_1|&=&|B_2| && ？ \\ \\ |B_1|&>&|B_2| && ？ \end{array}$

この時点で

「要素数」について分かっていることはありません。

直感的にも結果的にも

$\begin{array}{ccc} |B_1|&=&|B_2| \end{array}$

こうなることは分かりますが

これは定義から直接的に得られる結論じゃないです。

基底の定義から分かること

$3$ 次元の話ではありますが

$\begin{array}{ccc} (x,y,z)&=& x(1,0,0)+y(0,1,0)+z(0,0,1) \end{array}$ 　

「標準基底」を用いれば

$\begin{array}{ccc} (2,0,0),(0,3,0),(0,0,4) \\ \\ (1,2,0),(0,3,4),(5,0,6) \end{array}$

このような

「要素数が同じになる基底」は

特に難しい手順を必要とせず作れます。

そしてこの具体例を考えると

「要素数が同じになることはある」と言えて

$\begin{array}{ccc} a_1v_1+b_1v_2 &=& v_3 \\ \\ a_2v_1+c_2v_3 &=& v_2 \\ \\ b_2v_2+c_3v_3 &=& v_1 \end{array}$

更に「線形独立」を確認できる

$\begin{array}{ccc} a_1v_{11}+b_1v_{21} &=& v_{31} \\ \\ a_1v_{12}+b_1v_{22} &=& v_{32} \\ \\ \vdots \\ \\ a_1v_{1n}+b_1v_{2n} &=& v_{3n} \end{array}$

「連立方程式」の形を考えると

基本、同じ数にしかならないと推定できます。

（標準基底への変換手順が連立方程式そのもの）

線形結合と連立方程式

詳細は長くなるので省きますが

$\begin{array}{ccc} \begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} &=& c_1 \begin{pmatrix} v_{11} \\ v_{12} \\ v_{13} \end{pmatrix} + c_2 \begin{pmatrix} v_{21} \\ v_{22} \\ v_{23} \end{pmatrix} + c_3 \begin{pmatrix} v_{31} \\ v_{32} \\ v_{33} \end{pmatrix} \end{array}$

「次元」に差がある

つまり $n\neqm$ とした場合

$\begin{array}{ccc} \begin{pmatrix} e_1 \\ e_2 \\ 0 \end{pmatrix} &=& c_1 \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} + c_2 \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}+ c_3 \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \end{array}$

この解の中に

$\begin{array}{ccc} c_1+c_3 &=& e_1 \\ \\ c_2+c_3&=& e_2 \end{array}$

「任意の解が必要である」というのは

$\begin{array}{ccc} \left\{ \begin{array}{ccc} x+z&=& 1 \\ \\ y+z&=& 0 \end{array} \right. \end{array}$

直感的に理解できると思います。

（どれかを任意定数にしないと解が得られない）

この事実を踏まえると

$\begin{array}{lcl} B_1 &=& \{ v_1,v_2,...,v_n \} \\ \\ B_2 &=& \{ u_1,u_2,...,u_m \} \end{array}$

「基底」が $V$ の要素を全て表現できることから

（これは基底の存在定理と定義より明らか）

$\begin{array}{ccc} u_1&=& c_{11} v_1 +c_{12} v_2+\cdots + c_{1n} v_n \\ \\ u_2&=& c_{21} v_1 +c_{22} v_2+\cdots + c_{2n} v_n \\ \\ & & \vdots \\ \\ u_m&=& c_{m1} v_1 +c_{m2} v_2+\cdots + c_{mn} v_n \end{array}$

こうなることも明らかだと言えます。

とすると

$\begin{array}{ccc} c^*_1 u_1 + c^*_2 u_2 +\cdots + c^*_m u_m &=& \vec{0} \end{array}$

「線形独立」の定義を意識しつつ

（これらの定数は全て $0$ になるはず）

ちゃんと「線形独立」になるか

（まず ↑ の線形独立を用いず ↓ の線形結合を得る）

$\begin{array}{lclcl} c^*_1 u_1 &+& \cdots &+ & c^*_m u_m &=& \vec{0} \\ \\ c^*_1(c_{11} v_1 +\cdots + c_{1n} v_n) &+& \cdots &+ & c^*_m (c_{m1} v_1 +\cdots + c_{mn} v_n) &=& \vec{0} \end{array}$

以下のように式を変形し

$\begin{array}{ccc} (c^*_{1}c_{11} + c^*_{2}c_{21} + \cdots + c^*_{m}c_{m1} ) & v_1 \\ \\ (c^*_{2}c_{12} + c^*_{2}c_{22} + \cdots + c^*_{m}c_{m2} ) & v_2 \\ \\ \vdots \\ \\ (c^*_{n}c_{1n} + c^*_{n}c_{2n} + \cdots + c^*_{m}c_{mn} ) & v_n \end{array}$

「連立方程式」を考えて確認してみると

（線形独立なのでこれも $0$ になる必要がある）

$\begin{array}{ccc} c^*_{1}c_{11} + c^*_{2}c_{21} + \cdots + c^*_{m}c_{m1} &=& 0 \\ \\ c^*_{2}c_{12} + c^*_{2}c_{22} + \cdots + c^*_{m}c_{m2} &=& 0 \\ \\ \vdots \\ \\ c^*_{n}c_{1n} + c^*_{n}c_{2n} + \cdots + c^*_{m}c_{mn} &=& 0 \end{array}$

「変数 $c^*_k$ の数 $m$ 」と「式の数 $n$ 」から

例えば $n<m$ としてしまうと

「中身がなんでもいい解」が出てきてしまうので

（この任意定数解の詳細は長くなるので別の記事で）

$\begin{array}{ccc} c^*_k &=& t \end{array}$

このパターンでは

「任意定数 $c^*_k$ の存在」により

（ $v$ の方の線形独立から得られた結果）

$\begin{array}{ccc} c^*_1 u_1 + c^*_2 u_2 +\cdots + c^*_m u_m &=& \vec{0} \end{array}$

この「線形独立」の定義に矛盾する。

そんな結論が得られてしまいます。

（こちらの方の線形独立に合致しない）

連立方程式の任意定数と線形独立

ざっとまとめると

「基底」の定義と

「線形独立の判定式」から

$\begin{array}{lclcl} c^*_1 u_1 &+& \cdots &+ & c^*_m u_m &=& \vec{0} \\ \\ c^*_1(c_{11} v_1 +\cdots + c_{1n} v_n) &+& \cdots &+ & c^*_m (c_{m1} v_1 +\cdots + c_{mn} v_n) &=& \vec{0} \end{array}$

この式が得られて

「 $v$ の線形独立性」によりこうなるが

これは $n<m$ の場合では

「任意の定数解」を持つ連立方程式になるので

$\begin{array}{ccc} c^*_1 u_1 + c^*_2 u_2 +\cdots + c^*_m u_m &=& \vec{0} \end{array}$

こちらの「線形独立性」に矛盾してしまう。

（ $v$ の方から $u$ の線形独立性が否定される）

↑ の話を要約すると

こんな感じの内容になるんですが

これは $n<m$ の場合だけでなく

$\begin{array}{ccc} v_1&=& c_{11} u_1 +c_{12} u_2+\cdots + c_{1m} u_m \\ \\ v_2&=& c_{21} u_1 +c_{22} u_2+\cdots + c_{2m} u_m \\ \\ & & \vdots \\ \\ v_n&=& c_{n1} u_1 +c_{n2} u_2+\cdots + c_{nm} u_m \end{array}$

$n>m$ の場合でも

別方向から考えた同様の手順を踏めるので

$\begin{array}{ccc} c^*_{1}c_{11} + c^*_{2}c_{21} + \cdots + c^*_{n}c_{n1} &=& 0 \\ \\ c^*_{2}c_{12} + c^*_{2}c_{22} + \cdots + c^*_{n}c_{n2} &=& 0 \\ \\ \vdots \\ \\ c^*_{m}c_{1m} + c^*_{m}c_{2m} + \cdots + c^*_{n}c_{nm} &=& 0 \end{array}$

このパターンでも

同様の理由により矛盾が生じます。

等しくないと矛盾が生じる

以上より

$\begin{array}{lcl} B_1 &=& \{ v_1,v_2,...,v_n \} \\ \\ B_2 &=& \{ u_1,u_2,...,u_m \} \end{array}$

「線形独立」について確認できる

「連立方程式の解」を考えると

$\begin{array}{ccc} n&<&m \\ \\ n&>&m \end{array}$

このパターンでは矛盾が生じるので

（どの基底を比較してもこれだと矛盾が生じる）

$\begin{array}{ccc} n&=&m \end{array}$

結果

「基底の要素数」は１つの値に定まると言えます。

（基底は複数存在するためこうでなければならない）

基底の延長定理

これは「線形独立なベクトルの集合」

この存在を前提とする定理で

（要は部分空間がある状態）

$\begin{array}{ccc} \{ v_1,v_2,v_3,...,v_n \} \end{array}$

これが「 $V$ の基底にまで延長できる」

ということをこの定理は主張しています。

存在定理と次元数による必然

これは「存在定理」の証明で使った

$\begin{array}{ccc} v_{n+1}&\in&V\setminus \mathrm{Span}(\{ v_1,v_2,...,v_n \}) \end{array}$

『線形独立なベクトルの集合を作る操作』と

（基底になるまで不足分を補える）

$\begin{array}{ccc} | \mathrm{Basis}(V)| &=& N \end{array}$

「ベクトル空間の基底の要素数は同じ」という事実から

（ $\mathrm{Basis}(V)$ は $V$ の基底を返すとします）

$\begin{array}{lcl} n=N &\to& 基底 \\ \\ n<N &\to& 要素を１つ追加 \end{array}$

単純な場合分けで導くことができます。

（常に $n\leqN$ であるとします）

目次

ベクトル Vector

線型空間 Linear Space

線形空間の基本的な性質

線型性 Linearity

線型独立 Linearly Independent

線型従属

線形包 Liner Span

線形包の具体的な感覚

線形包はベクトル空間の部分集合になる

部分集合の線形包

部分集合であることの証明

基底 Basis

標準基底 Standard Basis

基底と標準基底

正規直交基底

基底の厳密な定義

基底の線形包

基底は定数と和で標準基底に変換可能

線形結合と連立方程式

基底の存在定理

前提の確認

ベクトル空間と例外

有限次元ベクトル空間では

直線では

平面や空間なら

線形包とそれ以外のベクトルの存在

線形独立なベクトルを選べる

線型従属とそれ以外

線形従属と線形包

線形独立になるはず

空間やそれ以上でも同様

線形包と線形独立

有限次元ベクトル空間の定義と操作の回数

有限次元の同値な定義

それぞれの定義と論理式

存在 ⇒ 有限

基底の要素数と無限集合

V を生成するとしたまま無限集合へ

集合の並びに制限は無い

最初だけではない

線形独立にできる限界がある

有限 ⇒ 存在

線形独立なベクトルを選べる

有限次元ベクトル空間と基底の存在

基底の複数存在定理

例外の処理

複数存在するだろう最小のサイズ

基底が１つしかないと仮定する

反例の構成

反例だと予想される集合の中身

反例だと予想される集合は基底であるか

基底は複数存在する

基底の要素数の唯一性

基底の存在と要素数

基底の定義から分かること

線形結合と連立方程式

連立方程式の任意定数と線形独立

等しくないと矛盾が生じる

基底の延長定理

存在定理と次元数による必然

$V$ を生成するとしたまま無限集合へ