|| 2変数以上の積分
変数が1個より多い時の「積分」の名前
3 変数以上はあまり使われません。
スポンサーリンク
目次
多重積分「2変数以上を積分する時の積分の名前」
逐次積分「変数を1個ずつ積分していくやり方」
フビニの定理「多重積分と逐次積分が一致する条件」
トネリの定理「フビニの定理の基礎になる条件」
二重級数「多重積分を有限に落とし込んだ形」
可積分「積分できるって意味の単語」
σ-有限「一意性を保証するやつ」
直積測度「二重級数などの感覚を厳密化したもの」
可測長方形「測度論で定義された長方形のこと」
ルベーグ積分「定義関数の積分を測度として計算」
多重積分 Multiple Integral
|| 2変数以上を積分する時の積分の呼び方
基本的に2変数の積分(二重積分)しか扱いません。
\begin{array}{llllll} \displaystyle \int_D f(z) \,dz &=&\displaystyle\int_D f(x,y) \,d(x,y) &=&\displaystyle\int\int_D f(x,y) \,dxdy \end{array}
\begin{array}{ccc} \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} a_k \, μ(D_k) \right\} \end{array}
たまーに三重積分と一般形は見ますが
あまり実用性はないですね。
\begin{array}{llllll} \displaystyle D&=&[a_1,b_1]×[a_2,b_2] \\ \\ V&=&\displaystyle \int\int_D f(x,y) \, dxdy \\ \\ \\ \displaystyle D&=&[a_1,b_1]×[a_2,b_2]×\cdots×[a_n,b_n] \\ \\ V&=&\displaystyle \int\int\cdots\int_D f(x_1,x_2,\cdots,x_n) \, dx_1dx_2\cdots dx_n \end{array}
1変数の積分が
『ほぼ線の長方形』の「集まり」から
『面積』を求めたのに対して
\begin{array}{llllll} \displaystyle f(x) \, dx \\ \\ f(x,y) \, dxdy\end{array}
2変数の積分は
『ほぼ線の直方体』の「集まり」から
『体積』を求める操作になります。
ちなみにこの「多重積分」ですが
「重積分」と呼ばれることもあります。
逐次積分 Iterated Integral
|| 変数を1個ずつ積分してく感じの積分
多重積分の基本的な計算方法のこと。
他の名前もあります(累次積分・反復積分)
\begin{array}{llllll} \displaystyle D&=&[a_1,b_1]×[a_2,b_2] \\ \\ \\ V&=&\displaystyle \int\int_D f(x,y) \, dxdy \\ \\ &=&\displaystyle \int_{a_2}^{b_2} \left( \int_{a_1}^{b_1} f(x,y) \, dx \right) \, dy \end{array}
「微分」で言うところの
『偏微分』みたいなものですね。
\begin{array}{llllll} \displaystyle \displaystyle \int\int_D f(x,y) \, dxdy &&?\\ \\ \displaystyle \int_{a_2}^{b_2} \left( \int_{a_1}^{b_1} f(x,y) \, dx \right) \, dy && 〇\end{array}
計算ってなると
基本的にこのやり方がメインになります。
多重積分と逐次積分は異なる
逐次積分と多重積分は
常に一致するわけではありません。
(まあだいたい一致するんですが)
\begin{array}{cll} xy^2 & & \left\{\begin{array}{lcl} -\infty≤x≤\infty \\ \\ -\infty≤y≤\infty \end{array} \right. \\ \\ \\ \displaystyle \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} && \left\{ \begin{array}{lcl} 0≤x≤1 \\ \\ 0≤y≤1 \end{array} \right. \end{array}
例えばこういうパターンでは
\begin{array}{llcllll} \displaystyle \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} xy^2\, dx \right) \, dy &=&0 \\ \\ \displaystyle \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} xy^2 \, dy \right) \, dx &=& \infty \end{array}
\begin{array}{llrllll} \displaystyle \int_{0}^{1} \left( \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dx \right) \, dy &=& \displaystyle -\frac{π}{4} \\ \\ \displaystyle \int_{0}^{1} \left( \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dy \right) \, dx &=& \displaystyle \frac{π}{4} \end{array}
逐次積分を行うと
順番によって積分値が変化します。
\begin{array}{llllll} \displaystyle \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dx&=&\displaystyle\left[ -\frac{x}{x^2+y^2} \right]_{0}^{1} \\ \\ &=&\displaystyle-\frac{1}{1+y^2} \\ \\ \\ \displaystyle \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dy&=&\displaystyle\left[ \frac{y}{x^2+y^2} \right]_{0}^{1} \\ \\ &=&\displaystyle\frac{1}{x^2+1} \end{array}
ちなみにこれの積分はこんな感じ。
(詳しい計算は長い上に本題から逸れるのでカット)
フビニの定理 Fubini’s Theorem
|| 積分可能なら逐次積分は多重積分と一致する
[a_1,b_1]×[a_2,b_2] の範囲で「 f が可積分」なら
(可積分は f が可測関数であることも意味する)
\begin{array}{llllll} \displaystyle D&=&[a_1,b_1]×[a_2,b_2] \\ \\ \\ V&=&\displaystyle \int\int_D f(x,y) \, dxdy \\ \\ &=&\displaystyle \int_{a_2}^{b_2} \left( \int_{a_1}^{b_1} f(x,y) \, dx \right) \, dy \\ \\ &=&\displaystyle \int_{a_1}^{b_1} \left( \int_{a_2}^{b_2} f(x,y) \, dy \right) \, dx \end{array}
「多重積分」と「逐次積分」は一致する
まあつまるところ
\begin{array}{lcl}\displaystyle \int_D \Bigl| f(x,y) \Bigr| \, dμ(x,y) &<& \infty \end{array}
「範囲 D 」内で「積分可能である」ことが
『逐次積分』して良い根拠だとこの定理は主張してます。
(計算結果は不明ですがこの状態を前提とする)
トネリの定理 Tonelli’s Theorem
|| 正の普通の関数なら多重積分と逐次積分は一致
「可測関数」で「非負(正)」ならいける
(可積分は条件に含まれず計算結果が無限でもいい)
\begin{array}{lcc} \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}a_k 1_{D_k}(x)&=& f(x) && 1点\\ \\ \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}a_k μ({D_k})&=& \displaystyle \int_D f(x) \, dμ(x) &&全域 \\ \\ \displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}a_k μ({D_k})&=& \displaystyle \int_D f(x,y) \, dμ(x,y) \end{array}
\begin{array}{lcl} \forall n\in N & 0≤a_n \end{array}
これはそのまんま
(有界な単調増加列は収束し極限は一意に定まる)
二重級数とコーシー積
多重積分と逐次積分の関係は
本質的には「二重級数」の話になります。
(つまりはコーシー積の話)
\begin{array}{llllll} \displaystyle \sum_{i=1}^{n}\sum_{j=1}^{m}a_{ij} &=& \displaystyle \begin{array}{c} \displaystyle \sum_{j=1}^{m}a_{1j} \\ \displaystyle\sum_{j=1}^{m}a_{2j} \\ \vdots \\ \displaystyle\sum_{j=1}^{m}a_{nj} \end{array} &=& \displaystyle \begin{array}{c} \displaystyle a_{11}+a_{12}+\cdots + a_{1m} \\ \\ a_{21}+a_{22}+\cdots + a_{2m} \\ \\ \vdots \\ \\ a_{n1}+a_{n2}+\cdots + a_{nm} \end{array} \end{array}
\begin{array}{llllll} \displaystyle \sum_{i=1}^{n}\sum_{j=1}^{m}a_{ij} &=& \displaystyle \sum_{j=1}^{m}\sum_{i=1}^{n}a_{ij} \end{array}
このような操作で矛盾が出ない
これが多重積分における定理の本質で
↑ はこれを実現するための条件になります。
ちなみに a_{ij} ですが
\begin{array}{llllll} \displaystyle a_{ij}&=& dxdyd(x,y)\end{array}
これはこの話の場合だと
「小さくできる直方体の体積」を意味します。
(小さくしつつ無限に集めて全体の体積にする感じ)
発想の元は絶対収束
「ルベーグ測度 μ^*(一意に定まる)」
\begin{array}{lcl} μ\Bigl( [a,b) \Bigr)&=&b-a \end{array}
\begin{array}{lcl} μ^*(I)&=&\displaystyle \inf \left\{ \sum_{n=1}^{\infty} μ(I_n) \,\middle| \, I⊂\bigcup_{n=1}^{\infty}I_n \right\} \end{array}
「定義関数 1_D 」「定義関数の積分」
(これらは疑問の余地が無いため定義になります)
\begin{array}{lcl} 1_D(x)&=& \left\{ \begin{array}{ccl} 1 && x\in D \\ 0 && x\not\in D \end{array} \right. \end{array}
\begin{array}{lcl} \displaystyle \int_{-\infty}^{\infty} 1_{[a,b)}(x) \,dμ(x) &=& b-a &=& μ\Bigl( [a,b) \Bigr) \end{array}
これらにより定義される
「単関数 φ 」「単関数の積分」により
\begin{array}{ccc} φ_n(x) &=& \displaystyle\sum_{k=1}^{n} a_k \, 1_{D_k}(x) \\ \\ \displaystyle\int_D φ_n(x) \, dμ(x) &=& \displaystyle\sum_{k=1}^{n} a_k \, μ(D_k) && \displaystyle D=\bigsqcup_{k=1}^{n}D_k \end{array}
「ルベーグ積分」は ↓ のように定義されていて
(単関数近似定理より φ_n の存在は保証される)
\begin{array}{ccc} \displaystyle \lim_{n\to\infty} φ_n(x) &=& f(x) \end{array}
\begin{array}{lcl} \displaystyle \int_{D}f(x) \,dμ(x) &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} a_k \, μ(D_k) \right\} \end{array}
「逐次積分」で大切なのは
\begin{array}{ccc} \displaystyle \sum_{i=1}^{n}\sum_{j=1}^{m}a_{ij} &=& \displaystyle \sum_{j=1}^{m}\sum_{i=1}^{n}a_{ij} \end{array}
「並び替えても同じになる」ですから
「絶対収束すれば良さそう」
これが自然な結論として導かれます。
実際
\begin{array}{ccc} 0&≤&|f(x)| && \mathrm{Fubini} \\ \\ 0 &≤& f(x) && \mathrm{Tonelli} \end{array}
「トネリの定理」も「フビニの定理」も
両方とも「絶対収束」に近い内容になっています。
(これと二重級数が分かると直感的に正しいと分かる)
可積分 Integrable
|| そのまんま積分できるって意味の単語
「ルベーグ可積分」とかいう定義された用語のこと
\begin{array}{llllll} \displaystyle \int_{D} \Bigl| f(x) \Bigr| \,μ(dx)&<&\infty \end{array}
これは要するに「絶対収束」のことで
「数列を並び替えても総和が変わらない」みたいな
そういう感じの話になります。
σ-有限 σ-finite
|| 一般性を損なわない程度の緩い条件
『測度の一意性を保証するための条件』のこと。
\begin{array}{llllll} \displaystyle (X,σ_X,μ) \,\, \mathrm{is} \,\, \mathrm{Measure \,\, Space} \end{array}
\begin{array}{llllll} \displaystyle (R,\mathrm{Borel}(R),μ_{\mathrm{Lebesgue}})&&\to&& \displaystyle\bigcup_{n∈N}[-n,n]=R \end{array}
\begin{array}{llllll} \displaystyle μ_{\mathrm{Lebesgue}}([-n,n])=2n&<&\infty \end{array}
「測度空間」に定義される概念で
(測度空間は完全加法性が保証されてる)
\begin{array}{llllll} \displaystyle I_1,I_2,I_3,...&∈&σ \end{array}
\begin{array}{llllll} \displaystyle \bigcup_{n=1}^{\infty}I_n&=&X \end{array}
\begin{array}{llllll} \displaystyle \forall n∈N &μ(I_n)<\infty \end{array}
↑ の条件を満たす時
その「測度空間は σ-有限である」と言います。
主に使われる場面は
「カラテオドリの拡張定理」などの証明です。
(測度の一意性を保証したいという要望から)
直積測度 Product Measure
|| 測度の掛け算的な操作の話
以下の条件を満たす M_{\mathrm{product}} が「直積測度」です。
(「多重積分」の一般形になります)
\begin{array}{llllll} X\times Y &=&\{ (x,y) \mid x∈X ∧ y∈Y \} \end{array}
\begin{array}{llllll} \displaystyle M_{\mathrm{product}}&=&μ_X\times μ_Y \\ \\ μ_{X\times Y}&=&μ_X\times μ_Y \end{array}
「測度空間」への「直積」操作
\begin{array}{llllll} \displaystyle I_X&∈&σ_X \\ \\ I_Y&∈&σ_Y \end{array}
\begin{array}{llllll} \displaystyle μ_{X\times Y}(I_X\times I_Y)&=&μ_X(I_X)μ_Y(I_Y) \end{array}
その自然な拡張としてこのように定義されています。
(測度空間 (X,σ_X,μ_X) \,\, (Y,σ_Y,μ_Y) 上の話)
この記事では
これで図形を表現して多重積分を説明する感じです。
(特にルベーグ積分はこの定義に依存します)
σ-有限測度上での直積測度
「直積測度」の元となる
「測度空間 (X,σ_X,μ_X) \,\, (Y,σ_Y,μ_Y) 」が
「σ-有限な測度空間」である時
\begin{array}{llllll} \displaystyle M_{\mathrm{product}}&=&μ_X\times μ_Y \end{array}
「直積測度 M_{\mathrm{product}} 」は一意に定まります。
(測度の一意性については別記事で)
この事実と「絶対収束」を利用したのが
「フビニの定理」「トネリの定理」で
\begin{array}{llllll} \displaystyle \int\int_D f(x,y) \, dxdy &=&\displaystyle \int_{a_2}^{b_2} \left( \int_{a_1}^{b_1} f(x,y) \, dx \right) \, dy \\ \\ \displaystyle \int\int_D f(x,y) \, dxdy&=&\displaystyle \int_{a_1}^{b_1} \left( \int_{a_2}^{b_2} f(x,y) \, dy \right) \, dx \end{array}
「極限の一意性」「測度の一意性」から
当然の結果としてこの結論が導かれます。
(現状では直感的に明らかだと分かる程度)
長方形 Rectangle
|| 面積を定義する最小単位
「図形」「集合」「区間」「面積の定義」から
\begin{array}{llllll} \displaystyle \mathrm{Rect}&⊂&X\times Y \end{array}
「長方形 \mathrm{Rect} 」は
\begin{array}{llllll} \displaystyle I_X&⊂&X \\ \\ I_Y&⊂&Y \end{array}
「区間 I_X,I_Y 」の直積として
\begin{array}{llllll} \displaystyle \mathrm{Rect}&=&I_X \times I_Y \\ \\ &=& \{ (x,y) \mid x∈I_X ∧ y∈I_Y \} \end{array}
「測度論」的には
このような形で定義されています。
(点を意味する座標 (x,y) の集合)
可測長方形 Measurable Rectangle
|| そのまま可測な長方形(集合)のこと
「面積を求めることができる長方形」のこと
\begin{array}{cccc} 長方形の面積&=&底辺×高さ \\ \\ \displaystyle |\mathrm{Rect}| &=& μ_X(I_X)μ_Y(I_Y) \end{array}
「可測である」という条件が付いただけで
\begin{array}{llllll} \displaystyle I_X&∈&σ_X \\ \\ I_Y&∈&σ_Y \end{array}
基本的には「長方形」の定義と同様です。
(この定理における図形はこれを拡張したもの)
ルベーグ積分 Lebesgue Integral
|| 単関数近似定理を根拠にした積分
明確に「測度」と関連付けられた積分のこと
\begin{array}{lcl} \displaystyle \int_{(-\infty,\infty)} 1_{[a,b)}(x) \,dμ(x) &=& μ\Bigl( [a,b) \Bigr) \\ \\ \displaystyle \int_{X\times Y} 1_{I_X\times I_Y}(x,y) \,dμ(x,y) &=& μ_{X\times Y}(I_X\times I_Y) \end{array}
「定義関数の積分」と「測度」の関係から
\begin{array}{lcl} \displaystyle\int_{X} f \, dx &\to& \displaystyle\int_{X} f \, dμ \\ \\ \displaystyle\int_{X\times Y} f \, dxdy &\to& \displaystyle\int_{X\times Y} f \, dμ \end{array}
「多重積分」と「逐次積分」は
\begin{array}{lcl} φ_n(x) &=& \displaystyle \sum_{k=1}^{n} c_k 1_{ I_k }(x) \\ \\ φ_n(x,y) &=& \displaystyle \sum_{k=1}^{n} c_k 1_{ ( I_X\times I_Y )_k }(x,y) \end{array}
「単関数」の性質と
\begin{array}{rcl} φ_n(x,y) &≤& f(x,y) \\ \\ \displaystyle \lim_{n\to\infty} φ_n(x,y) &=& f(x,y) \end{array}
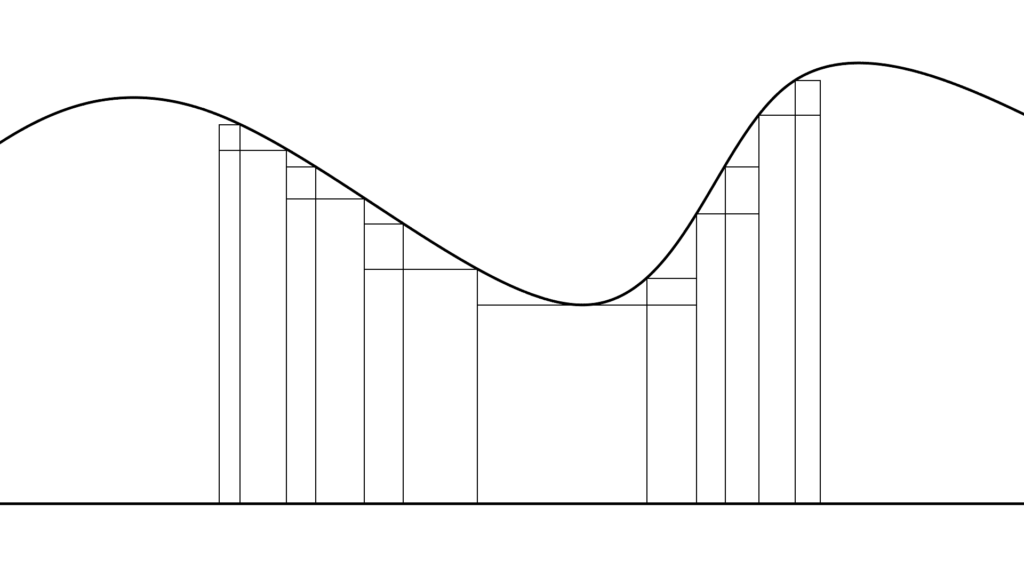
「単関数近似定理」を根拠として
\begin{array}{ccc} I &=& \displaystyle \bigsqcup_{k=1}^{n} I_k \\ \\ \displaystyle \int_{I} φ_n(x) \, dμ(x) &=& \displaystyle \sum_{k=1}^{n} c_k μ(I_k) \end{array}
「単関数の積分」から
\begin{array}{lcl} \displaystyle \int_{I} f(x) \,dμ(x) &=& \displaystyle \sup\left\{ \int_{I} φ_n(x) \, dμ(x) \right\} \\ \\ \displaystyle \int_{I} f(x) \,dμ(x) &=& \displaystyle \sup\left\{ \sum_{k=1}^{n} c_k μ(I_k) \right\} \end{array}
「測度」を使うことにより
このような形で厳密に定義されています。
(測度の一意性から順序交換の根拠が得られる)
ルベーグ積分の線型性
「多重積分」を厳密に定義する時
\begin{array}{lcl} \displaystyle\int f &=& \displaystyle \int f^+ - \int f^- && ? \\ \\ \displaystyle\int f &=& \displaystyle \int \Bigl( f^+ + (-1)f^- \Bigr) && 〇 \end{array}
「一般の可測関数」について考えたくなるので
( f^+ は正の部分 f^- は負の部分で両方とも正)
\begin{array}{ccc} f(αx+βy) &=& αf(x) + βf(y) \\ \\ \displaystyle \int αf+βg &=& \displaystyle α\int f + β\int g \\ \\ \displaystyle \int f^+ +(-1)f^- &=& \displaystyle \int f^+ + (-1)\int f^- \end{array}
「ルベーグ積分」を考える上で
これはほぼ必須の操作になります。
(見やすさのために略記)
線型性についての雑な証明
厳密な証明については
長くなるので別記事で行います。
\begin{array}{ccc} f(αx+βy) &=& αf(x) + βf(y) \\ \\ f(αx+βy) &=& f(αx) + f(βy) \\ \\ &=& αf(x) + βf(y) \end{array}
この記事では
「線型性」を構成する「斉次性」「加法性」について
\begin{array}{rcr} φ_n(x) &=& \displaystyle \sum_{k=1}^{n} c_k 1_{D_k} (x) \\ \\ αφ_n(x) &=& \displaystyle α\sum_{k=1}^{n} c_k 1_{D_k} (x) \end{array}
「非負単関数」までしか扱いません。
(一般の可測関数でも線型性は成立)
単関数積分の斉次性の証明
詳しくはやりませんが
\begin{array}{ccc} \displaystyle α\sum_{k=1}^{n} c_k 1_{D_k} (x) &=& \displaystyle \sum_{k=1}^{n} αc_k 1_{D_k} (x) \end{array}
「総和の斉次性」さえ理解していれば
「単関数のルベーグ積分」が「斉次性」を持つ
(正の単関数としたいので 0≤α とする)
\begin{array}{lclcl} \displaystyle \int αφ_n(x) &=& \displaystyle \sum_{k=1}^{n} (α c_k) μ(D_k) \\ \\ &=& \displaystyle \sum_{k=1}^{n} α c_k μ(D_k) \\ \\ &=& \displaystyle α\sum_{k=1}^{n} c_k μ(D_k) &=& \displaystyle α\int φ_n(x) \end{array}
この事実については
特に疑問なくすぐ分かると思います。
(有限総和の斉次性については明らかなので省略)
単関数積分の加法性の証明
これも ↑ と同様
\begin{array}{lcl} φ_n(x) &=& \displaystyle \sum_{k=1}^{n} a_k 1_{D_k} (x) \\ \\ ψ_n(x) &=& \displaystyle \sum_{k=1}^{n} b_k 1_{D_k} (x) \end{array}
「非負の単関数」で考えていくと
「細分割」という概念を認めれば
\begin{array}{ccccl} i≠j⇒D_i ∩ D_j=∅ && \to && \displaystyle D=\bigcup_{k=1}^{n}D_k \\ \\ i≠j⇒D_i ∩ D_j=∅ && ← && \displaystyle D=\bigsqcup_{k=1}^{n}D_k \end{array}
「共通の積分範囲 D 」の
「共通の分割 D_k 」で単関数を再定義できるので
その再定義により得られた単関数を比較すれば
\begin{array}{ccc} φ_n+ψ_n \\ \\ \displaystyle \sum_{k=1}^{n} a_k 1_{D_k} (x) + \sum_{k=1}^{n} b_k 1_{D_k} (x) &=& \displaystyle \sum_{k=1}^{n} (a_k+b_k) 1_{D_k} (x) \end{array}
「単関数の和」の形と
\begin{array}{lcl} \displaystyle \int_D φ_n + \int_D ψ_n &=& \displaystyle \sum_{k=1}^{n} a_k μ(D_k) + \sum_{k=1}^{n} b_k μ(D_k) \end{array}
「非負単関数の積分」の定義により
\begin{array}{lcl} \displaystyle \sum_{k=1}^{n} a_k μ(D_k) + \sum_{k=1}^{n} b_k μ(D_k) &=& \displaystyle \sum_{k=1}^{n} a_k μ(D_k) + b_k μ(D_k) \\ \\ &=& \displaystyle \sum_{k=1}^{n} (a_k + b_k) μ(D_k) \\ \\ &=& \displaystyle \int_D \left( \sum_{k=1}^{n} (a_k+b_k) 1_{D_k} (x) \right) \end{array}
これはこのような流れで証明できます。
(これを基礎として非負可測関数の場合は証明される)
多重積分の定理の証明
以上の話を理解していれば
多重積分の各定理は証明できます。
\begin{array}{lcl} 0≤|f(x)| &\to& 逐次積分が一致 \\ \\ 0≤f(x) &\to& 逐次積分が一致 \end{array}
具体的には
(厳密にはσ-有限な測度が一意に定まる)
\begin{array}{lcl} μ\Bigl( [a,b) \Bigr) &=& b-a \\ \\ μ^*(I)&=&\displaystyle \inf \left\{ \sum_{n=1}^{\infty} μ(I_n) \,\middle| \, I⊂\bigcup_{n=1}^{\infty}I_n \right\} \\ \\ μ_X \times μ_Y (I_X \times I_Y) &=& μ_X(I_X) μ_Y(I_Y) \end{array}
\begin{array}{ll} \displaystyle \lim_{n\to\infty} φ_n(x) &=& f(x) \end{array}
\begin{array}{lcl} \displaystyle \sum_{n=1}^{\infty}|a_n| &<& \infty \end{array}
そして ↓ の一意性を利用することで
\begin{array}{lcl} 1_D(x)&=& \left\{ \begin{array}{ccl} 1 && x\in D \\ 0 && x\not\in D \end{array} \right. \end{array}
\begin{array}{lcl} \displaystyle \int_{-\infty}^{\infty} 1_{[a,b)}(x) \,dμ(x) &=& b-a &=& μ\Bigl( [a,b) \Bigr) \end{array}
「一意性がある状態」を維持しながら
欲しい結論に寄せていくという形でこれは証明できます。
(要するに良い感じの定義が定理の本質)
多重積分の問題点
「多重積分」の問題点は
『多重積分の解が複数存在する』こと
(測度・面積を求める関数が一意に定まらないこと)
\begin{array}{llcllll} \displaystyle \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} xy^2\, dx \right) \, dy &=&0 \\ \\ \displaystyle \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} xy^2 \, dy \right) \, dx &=& \infty \end{array}
\begin{array}{llrllll} \displaystyle \int_{0}^{1} \left( \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dx \right) \, dy &=& \displaystyle -\frac{π}{4} \\ \\ \displaystyle \int_{0}^{1} \left( \int_{0}^{1} \frac{x^2-y^2}{\left( x^2+y^2 \right)^2} \, dy \right) \, dx &=& \displaystyle \frac{π}{4} \end{array}
つまり『逐次積分が一致するとは限らない』ことで
(この原因がσ-有限ではないからだと推定)
\begin{array}{lcccl} 0≤f(x,y) &&→&& \mathrm{Toneli} \\ \\ \displaystyle 0≤|f(x,y)| &&→&& \mathrm{Fubini} \end{array}
各定理は
『どれが答えか分からない』この問題を解消するための
「計算結果が一致する条件」を求めたものになります。
多重積分と逐次積分の厳密な定義
この話を進めるために
\begin{array}{ccc} \displaystyle \int_D f(z) \,dz &=&\displaystyle\int_D f(x,y) \,d(x,y) &=&\displaystyle\int\int_D f(x,y) \,dxdy \end{array}
まずこれの曖昧さを取り除くため
良い感じの明確な定義を行っておきます。
( ↓ の定義は各定理が明確に関わる定義)
具体的には
「測度」と「直積測度」
「単関数近似定理」「ルベーグ積分」を使って
\begin{array}{ccc}\displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} a_k \, μ(D_k) \right\} \end{array}
より厳密に取り扱えるよう再定義してみます。
(これにより明確にσ-有限などの条件が推定できる)
多重積分の定義
リーマン積分的な感覚だと
\begin{array}{ccc} \displaystyle \int_D f(z) \,dz &=&\displaystyle\int_D f(x,y) \,d(x,y) &=&\displaystyle\int\int_D f(x,y) \,dxdy \end{array}
このように表現できる「多重積分」という概念は
(この時点じゃまだ定義がそこそこ曖昧)
\begin{array}{ccccl} D &=& I_X\times I_Y &&D⊂ X\times Y \\ \\ D&=& \displaystyle \bigsqcup_{k=1}^{n} D_k && D_k=(I_X\times I_Y)_k \end{array}
記号をこのように定めると
\begin{array}{ccc} μ_{X}\times μ_{Y}(I_X\times I_Y)&=&μ_X(I_X)μ_Y(I_Y) \end{array}
「直積測度空間」上の「ルベーグ積分」として
(この時点で f に可測関数という制限が付く)
\begin{array}{lcccl} \displaystyle \int_{X\times Y}f \,dμ &=& μ(D) && fが定義関数 \\ \\ \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle \sum_{k=1}^{n} a_k \, μ(D_k) && fが単関数 \\ \\ \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} a_k \, μ(D_k) \right\} && fが非負の可測関数 \\ \\ \end{array}
「単関数の積分」から
このような形で厳密に定義できます。
(直積測度により可測長方形の面積として定義できる)
負になり得る一般の可測関数
↑ までは直感的にも明確
なので「一般の可測関数」の場合は
\begin{array}{lclcl} f^+&=&\displaystyle\max\{0,f\} && 負の部分が全て0 \\ \\ f^-&=&\displaystyle\max\{0,-f\} &&正の部分が全て0 \end{array}
「負の値」を排除するために
「正になる部分」と「負になる部分」に分け
\begin{array}{ccc} \displaystyle \int_{X\times Y}f \,dμ &=&\displaystyle \int_{X\times Y}f^+ \,dμ - \int_{X\times Y}f^- \,dμ \end{array}
「非負可測関数の分割」という形で
「線型性」を使ってこのように定義してみます。
(現時点では問題が無さそうな定義)
逐次積分の定義
「逐次積分」は ↑ を分解してみたもので
(直積の分解を試してみた感じ)
\begin{array}{lccclcl} μ_{X\times Y}=μ_Xμ_Y &&\to&& \displaystyle \int_Y \left( \int_X f(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ μ_{X\times Y}=μ_Xμ_Y &&\to&& \displaystyle \int_X \left( \int_Y f(x,y) \,dμ(y) \right) \,dμ(x) \end{array}
それぞれこのように
「1変数で表現したもの」が厳密な定義になります。
(片方の変数を固定すればルベーグ積分の定義そのまま)
多重積分と逐次積分の一致
↑ の定義は直感的かつ単純ですが
まだ2つに明確な関連が無いので
\begin{array}{lcl} \displaystyle \int_{X\times Y}f \,dμ &=&\displaystyle \int_Y \left( \int_X f \,dμ(x) \right) \,dμ(y) \\ \\ \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle \int_X \left( \int_Y f \,dμ(y) \right) \,dμ(x) \end{array}
こうなるかどうかは今のところ不明です。
なのでこの等式の成立については
きちんと確認する必要があります。
可測関数 f が定義関数の場合
まず根本となる
\begin{array}{lcl} 1_{I_X\times I_Y}(x,y) &=& 1_{I_X}(x)1_{I_Y}(y) & & I_X \times I_Y & I_X & I_Y \\ &{} & {}& & ↓ & ↓ & ↓{} \\ 1_{D}(x,y) &=& 1_A(x)1_B(y) & & D & A & B \end{array}
「定義関数」から確認しておくと
( 1_{D}(x,y) は (x,y)\in D で 1 になるとします)
\begin{array}{lcl} \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle μ(D) \\ \\ \displaystyle \int_{X\times Y} 1_{D}(x,y) \,dμ(x,y) &=& \displaystyle μ_{X\times Y}(A\times B) \end{array}
まず「多重積分」はこうなると言えます。
( D が可測集合である場合に定義できる)
\begin{array}{lcl} \displaystyle \int_Y \left( \int_X f\,dμ(x) \right) \,dμ(y) &=& \displaystyle \int_Y \left( \int_X 1_{D}(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ &=& \displaystyle \int_Y \left( \int_X 1_{A}(x) 1_B(y) \,dμ(x) \right) \,dμ(y) \\ \\ &=& \displaystyle \int_Y \left( 1_B(y) \int_X 1_{A}(x) \,dμ(x) \right) \,dμ(y) \\ \\ \\ &=& \displaystyle \int_Y 1_B(y) μ_X(A) \,dμ(y) \\ \\ &=& \displaystyle μ_X(A) \int_Y 1_B(y) \,dμ(y) \\ \\ &=&μ_X(A)μ_Y(B) \end{array}
そして「逐次積分」はこうなるので
(詳しい話は長くなるのでここではざっくり)
以上の結果から
\begin{array}{lcl} \displaystyle \int_{X\times Y} 1_{D}(x,y) \,dμ(x,y) &=& \displaystyle μ_{X\times Y}(A\times B) \\ \\ \displaystyle \int_Y \left( \int_X 1_{D}(x,y) \,dμ(x) \right) \,dμ(y) &=&μ_X(A)μ_Y(B) \\ \\ \displaystyle \int_X \left( \int_Y 1_{D}(x,y) \,dμ(y) \right) \,dμ(x) &=&μ_Y(B)μ_X(A) \end{array}
「直積測度」の定義より
「多重積分と逐次積分は一致する」と言えます。
(測度の直積じゃないなら一致するとは限らない)
可測関数 f が単関数の場合
↑ の話から直感的には明らかですが
\begin{array}{ccl} φ_n(x,y) &=& \displaystyle \sum_{k=1}^{n} c_k 1_{D_k}(x,y) \\ \\ \displaystyle\int_D φ_n(x,y) \,dμ(x,y) &=& \displaystyle \sum_{k=1}^{n} c_k μ_{X\times Y}(D_k) \end{array}
こちらも念のため確認しておきます。
(これが実際の計算に近い形になります)
\begin{array}{lcl} \displaystyle \int_{X\times Y} 1_{D}(x,y) \,dμ(x,y) &=& \displaystyle μ_{X\times Y}(A\times B) \\ \\ \displaystyle \int_Y \left( \int_X 1_{D}(x,y) \,dμ(x) \right) \,dμ(y) &=&μ_X(A)μ_Y(B) \\ \\ \displaystyle \int_X \left( \int_Y 1_{D}(x,y) \,dμ(y) \right) \,dμ(x) &=&μ_Y(B)μ_X(A) \end{array}
使う式変形は ↑ の結果に寄せるだけ。
足し算である単関数
というわけで
まず「多重積分」についてですが
\begin{array}{lcl} \displaystyle\int_D f \,dμ &=& \displaystyle\int_D φ_n(x,y) \,dμ(x,y) \\ \\ &=& \displaystyle \sum_{k=1}^{n} c_k μ_{X\times Y}(D_k) \end{array}
こちらは特に何をするでもなく
そのまま定義から求めることができます。
「逐次積分」については
\begin{array}{lcl} \displaystyle \int \sum_{k=1}^{2} c_kf_k &=& \displaystyle \int c_1f_1 + \int c_2f_2 \\ \\ &=& \displaystyle c_1\int f_1 + c_2\int f_2 \\ \\ &=&\displaystyle\sum_{k=1}^{2} c_k\int f_k \end{array}
これを飲み込めるなら
(見やすさ重視で略記してます)
\begin{array}{lcl} \displaystyle \int_Y \left( \int_X f \,dμ(x) \right) \,dμ(y) &=& \displaystyle \int_Y \left( \int_X φ_n(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ &=& \displaystyle \int_Y \left( \int_X \sum_{k=1}^{n} c_k 1_{D_k}(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ \\ &=& \displaystyle \int_Y \left( \sum_{k=1}^{n} c_k \int_X 1_{D_k}(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ &=& \displaystyle \sum_{k=1}^{n} c_k\int_Y \left( \int_X 1_{D_k}(x,y) \,dμ(x) \right) \,dμ(y) \end{array}
このようにすれば
「定義関数」の話にできるため
意外と単純な式変形で
\begin{array}{lcl} \displaystyle \int_{X\times Y} φ_n(x,y) \,dμ(x,y) &=& \displaystyle\sum_{k=1}^{n} c_k μ_{X\times Y}(D_k) \\ \\ \displaystyle \int_Y \left( \int_X φ_n(x,y) \,dμ(x) \right) \,dμ(y) &=&\displaystyle\sum_{k=1}^{n} c_kμ_X(A_k)μ_Y(B_k) \\ \\ \displaystyle \int_X \left( \int_Y φ_n(x,y) \,dμ(y) \right) \,dμ(x) &=&\displaystyle\sum_{k=1}^{n} c_kμ_Y(B_k)μ_X(A_k) \end{array}
この結論を導くことができます。
(こちらも測度の直積が定義されてなければならない)
トネリの定理と多重積分の定義
↑ の話を続けていくと
今度は「非負の可測関数」の話になるわけですが
\begin{array}{ccccl} 0 &≤& \displaystyle f(x,y) &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} c_k \, 1_{D_k}(x,y) \right\} \\ \\ && \displaystyle \int_{X\times Y}f(x,y) \,dμ &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} c_k \, μ(D_k) \right\} \end{array}
実はこのパターンの話が
そのまま「トネリの定理」になります。
分かり辛いですが
証明自体はわりとシンプルで
\begin{array}{lcc} \displaystyle\lim_{n\to\infty} φ_n(x,y) &=&f(x,y) \\ \\ \displaystyle\lim_{n\to\infty} \int_D φ_n(x,y) dμ(x,y) &=&\displaystyle \int_D f(x,y) \,dμ(x,y) \end{array}
「単関数近似定理」を理解していれば
(単関数は非負であれば単調増加列)
\begin{array}{lcl} \displaystyle\lim_{n\to\infty} \int_D φ_n(x,y) dμ(x,y) &=& \displaystyle \int_D \left(\lim_{n\to\infty} φ_n(x,y) \right) dμ(x,y) \end{array}
「極限と積分の交換」が可能な条件下で
(一般的には交換できない)
\begin{array}{lclcl} \displaystyle \int_{X\times Y} φ_n(x,y) \,dμ(x,y) &=&\displaystyle \int_Y \left( \int_X φ_n(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ \displaystyle \int_{X\times Y} φ_n(x,y) \,dμ(x,y) &=&\displaystyle \int_X \left( \int_Y φ_n(x,y) \,dμ(y) \right) \,dμ(x) \end{array}
「単関数での一致」という
↑ で得られた事実をそのまま適用すれば
(以下見やすさのために略記)
\begin{array}{lclcl} \displaystyle \lim_{n\to\infty}\int_{X\times Y} φ_n &=&\displaystyle \lim_{n\to\infty}\int_Y \left( \int_X φ_n \right) \\ \\ \displaystyle \lim_{n\to\infty}\int_{X\times Y} φ_n &=&\displaystyle \lim_{n\to\infty}\int_X \left( \int_Y φ_n \right) \end{array}
「非負可測関数」における
\begin{array}{lcl} \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_Y \left( \int_X f(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_X \left( \int_Y f(x,y) \,dμ(y) \right) \,dμ(x) \end{array}
「多重積分と逐次積分の一致」は
わりと簡単に示すことができます。
(これに必要な各条件がトネリの定理の前提になる)
トネリの定理で必要になる前提を整理
以上のことを踏まえると
\begin{array}{ccc} \displaystyle \int_{X\times Y}f \,dμ &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} a_k \, μ_{X\times Y}(D_k) \right\} \end{array}
まず「ルベーグ積分」で積分される
「可測関数 f の存在」を保証する基盤として
\begin{array}{lcl} μ_{X\times Y} &=& μ_Xμ_Y \end{array}
「直積測度 μ_{X\times Y} の存在」を保証するために
\begin{array}{lll} X & σ_X & μ_X \\ \\ Y & σ_Y & μ_Y \end{array}
まずこれらは「測度空間」であることが求められます。
(この辺りの詳細は測度論の話になるので省略)
加えて
「直積測度」には「一意性」が求められるので
\begin{array}{lcl} \begin{array}{lcl} μ_X &1つだけ \\ \\ μ_Y &1つだけ \end{array} &&\to&& μ_{X\times Y}&1つだけ \end{array}
この「直積測度」の一意性を保証するために
\begin{array}{lcl} μ_{X\times Y}^1 &=& μ_Xμ_Y \\ \\ μ_{X\times Y}^2 &=& μ_Xμ_Y \\ \\ &\vdots \end{array}
「測度 μ_X,μ_Y 」は
「σ-有限」である必要があると言えます。
(これも直積測度の定義の話なので詳細はカット)
そして以上を前提とすると
「可測集合上の話」になるので
\begin{array}{lcl} 普通の関数 &\to& 可測関数 \end{array}
「ほぼ全ての普通の関数」を意味する
「可測関数」を全て扱えることになります。
(一意性を実現しようという方針からこれに繋がる)
ただこの時点では
「積分する関数 f 」に特に制限が無いので
\begin{array}{lcl} fが無制限 &\to& fは非負可測関数 \end{array}
「定義関数」「単関数」の流れから
「非負(正)の可測関数である」として
欲しい結果が得られるか確認
\begin{array}{lcl} \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_Y \left( \int_X f(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_X \left( \int_Y f(x,y) \,dμ(y) \right) \,dμ(x) \end{array}
↑ で示したように
「多重積分と逐次積分の一致」という
欲しかった結果が得られたことから
\begin{array}{lcl} 多重積分=逐次積分 &&←&& \left\{ \begin{array}{ll} σ\text{-}有限測度空間の直積 \\ \\ 積分されるのは非負値可測関数 \end{array} \right. \end{array}
「σ-有限測度空間」と「非負値可測関数」
これらが必要な前提になるということが分かります。
フビニの定理と多重積分の定義
「非負可測関数」についてはわかったので
最後は「一般の可測関数」について考えてみます。
\begin{array}{ccl} \displaystyle f(x,y) &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} c_k \, 1_{D_k}(x,y) \right\} \\ \\ \displaystyle \int_{X\times Y}f(x,y) \,dμ(x,y) &=& \displaystyle\sup \left\{ \sum_{k=1}^{n} c_k \, μ(D_k) \right\} \end{array}
「トネリの定理」の結果を見れば分かる通り
\begin{array}{lcl} \displaystyle \int_{X\times Y} |f(x,y)| \,dμ(x,y) &<& \infty \end{array}
「ルベーグ可積分」という条件の有無に関わらず
「トネリの定理」を適用しさえすれば
\begin{array}{lcl} \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_Y \left( \int_X f(x,y) \,dμ(x) \right) \,dμ(y) \\ \\ \displaystyle \int_{X\times Y} f(x,y) \,dμ(x,y) &=&\displaystyle \int_X \left( \int_Y f(x,y) \,dμ(y) \right) \,dμ(x) \end{array}
「非負値可測関数」までは
確実にこうなると言えます。
(負の可測関数が混ざると分からない)
一般の可測関数の時だけ不明瞭
問題となるのは
「一般の可測関数」の場合で
\begin{array}{lclcl} f^+&=&\displaystyle\max\{0,f\} && 負の部分が全て0 \\ \\ f^-&=&\displaystyle\max\{0,-f\} &&正の部分が全て0 \end{array}
\begin{array}{lcl} \displaystyle \int_D f \,dμ &=& \displaystyle \int_D f^+ \,dμ - \int_D f^- \,dμ \end{array}
「非負可測関数」により定義されてはいますが
これはこのままでは扱い辛いです。
(負の場合どうなるか不明)
非負可測関数の場合は分かっている
「非負可測関数」の話にするために
それぞれ分解して考えてみると
\begin{array}{lcl} \displaystyle \int_D f \,dμ &=& \displaystyle \int_D f^+ \,dμ - \int_D f^- \,dμ \end{array}
「トネリの定理」より
\begin{array}{lcl} \displaystyle \int_{X\times Y} f^+ \,dμ^* &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ \\ \\ \displaystyle \int_{X\times Y} f^- \,dμ^* &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ \end{array}
それぞれ「正 f^+ 」と「負 f^- 」の積分については
「多重積分と逐次積分が一致する」
これは間違いないと言えます。
可測関数のルベーグ積分と引き算
「トネリの定理」より
「非負可測関数」で ↓ のようになることは明らか
(この部分だけ見ると多重積分と逐次積分は一致)
\begin{array}{lcl} \displaystyle \int_{X\times Y} f^+ \,dμ^* &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ \\ \\ \displaystyle \int_{X\times Y} f^- \,dμ^* &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ \end{array}
ということは
\begin{array}{lcl} \displaystyle \int_D f \,dμ &=& \displaystyle \int_D f^+ \,dμ - \int_D f^- \,dμ \end{array}
「一般の可測関数」の積分では
少なくとも「積分値が両方とも有限」であれば
\begin{array}{lcl} \displaystyle \int_D f \,dμ &=& \displaystyle \int_D f^+ \,dμ - \int_D f^- \,dμ \\ \\ &=& \displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ - \int_Y \left( \int_X f^- \,dμ \right) \,dμ \\ \\ &=& \displaystyle \int_Y \left( \left( \int_X f^+ \,dμ \right) - \left( \int_X f^- \,dμ \right) \right) \,dμ \\ \\ &=& \displaystyle \int_Y \left( \int_X \left( f^+ - f^- \right) \,dμ \right) \,dμ \end{array}
「ルベーグ積分の線型性」を認めるなら
「多重積分と逐次積分は一致する」と言えます。
(この時の積分順序は交換しても同じなのでいずれも成立)
\begin{array}{lcl} \displaystyle \int_D f^+ \,dμ - \int_D f^- \,dμ \end{array}
しかし「積分値が有限でない」場合
これには問題が生じるので
まだ無条件で一致するとは言えません。
不定形の排除
まず確実に言えることは
\begin{array}{ccc} \displaystyle \int_D f^+ \,dμ &-& \displaystyle\int_D f^- \,dμ \\ \\ \infty &-& \infty \end{array}
これは定義できないということで
\begin{array}{ccc} \displaystyle \int_D f^+ \,dμ < \infty &\mathrm{or}& \displaystyle \int_D f^- \,dμ < \infty \end{array}
それ故に
こんな条件が付くのは間違いないと言えます。
(まだルベーグ可積分の条件より緩い)
片方の積分値が無限になる場合
両方とも無限になる
\begin{array}{ccc} \displaystyle \int_D f^+ \,dμ &-& \displaystyle\int_D f^- \,dμ \\ \\ \infty &-& \infty \end{array}
このパターンでは明らかにダメですが
\begin{array}{ccc} \displaystyle \int_D f^+ \,dμ &-& \displaystyle\int_D f^- \,dμ \\ \\ \infty & & α \\ \\ α & & \infty \end{array}
これらのパターンで大丈夫かどうか
現時点ではよく分かっていません。
しかし「正 f^+ と負 f^- の積分」の場合
「逐次積分と多重積分が一致する」
これはすでに分かっているので
\begin{array}{lcl} \displaystyle \int_{X\times Y} f^+ \,dμ^* &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ &=&\displaystyle \int_Y \left( \int_X f^+ \,dμ \right) \,dμ \\ \\ \displaystyle \int_{X\times Y} f^- \,dμ^* &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ &=&\displaystyle \int_X \left( \int_Y f^- \,dμ \right) \,dμ \end{array}
等式はこのまま使えますから
そのままの形で計算できます。
\begin{array}{ccccr} \displaystyle \int_D f^+ \,dμ &-& \displaystyle\int_D f^- \,dμ \\ \\ \infty &- & α &=& \infty \\ \\ α & - & \infty &=& -\infty \end{array}
するとこれらが一致するという結果は
わりと単純な形で求めることができるため
このパターンでは問題なく一致することが分かります。
結果としてルベーグ可積分の条件が必要
以上の話をまとめると
「両方とも無限にならない」
これが条件になると分かるため
\begin{array}{ccccc} |f| &=& f^+ &+& f^- \\ \\ \displaystyle \int_D |f| \,dμ &=& \displaystyle \int_D f^+ \,dμ &+& \displaystyle\int_D f^- \,dμ \end{array}
その結果として
それを意味する「ルベーグ可積分」
\begin{array}{lcl} \displaystyle \int_{X\times Y} |f| \,dμ &<& \infty \end{array}
あるいは
「無限」になる場合も定義する
「ルベーグ積分可能」というのが
\begin{array}{lcl} \displaystyle \int_{X\times Y} f^+ \,dμ < \infty &∨& \displaystyle \int_{X\times Y} f^- \,dμ < \infty \end{array}
「一般の可測関数」の場合における
「多重積分と逐次積分の一致条件」になります。
(まあつまり矛盾を排除した定義がこれということ)
