|| 何かの中身を決めること
「名前」とか「どういうものか」とかを決めます
スポンサーリンク
定義の大まかな分類
これは大きく分類すると
\begin{array}{ccl} 直感的定義 && 手順は無く正確かは怪しい \\ \\ 形式的定義 && 厳密な手順があり正確 \end{array}
こんな風に分けることができます。
(直感的な定義の中に形式的定義は含まれます)
直感的な意味での定義
これは人間の感覚に根差す概念なので
\begin{array}{lcl} \mathrm{Definire} & 境界を引く \\ \\ \mathrm{Define} & 定義する \end{array}
当然、大昔から存在していて
(語源は定義する対象を切り分ける感覚から来ている)
\begin{array}{ccc} \mathrm{Difinire} && \mathrm{Horismos} && \mathrm{Define} \\ \\ 切り分け &\to& 本質 &\to& 意味 \end{array}
「ヒルベルト」さんの形式主義が浸透するまでは
\begin{array}{ccc} 直感的定義 & \left\{ \begin{array}{rcc} 形式的定義 \\ \\ 非形式的定義 \end{array} \right. \end{array}
こういった分類はありませんでした。
(現代では形式的定義の比重が少し重い)
古代から続く定義の方法
「形式を軸とした分類」はありませんでしたが
「定義の方法」自体は確立されていて
\begin{array}{ccc} 惑星 &=& \{ 水星,金星,火星,木星,土星\} \end{array}
このような「列挙型」や
(この列挙型が特に古い)
\begin{array}{lcll} 概念 && 属 & 種差 \\ \\ \\ 人間 && 動物&理性的 \\ \\ りんご && 果物 & 酸っぱい \end{array}
「条件型」と呼ばれる定義方法は
紀元前から既に存在していました。
ただ、古い時代では
\begin{array}{lcl} 列挙型 && 具体的なものを並べただけ \\ \\ 条件型 && 概念の本質を抜き出している \end{array}
「本質(条件)」を元にした定義が重要視されていて
「列挙型」は定義未満と見なされていたようです。
Port-Royal 論理学
本格的にこの2つの関係を述べたのが
(厳密には論理として落とし込んだのが)
\begin{array}{lcl} 条件が少ない &\to& 要素数が多い \\ \\ 条件が多い &\to& 要素数が少ない \end{array}
17世紀ごろに出てきたこの論理学で
\begin{array}{lcl} 果物,赤い,甘い,酸っぱい &\to& 絞れる \\ \\ 果物 &\to& 絞れない \end{array}
これにより
「条件型」と「列挙型」の関係が
\begin{array}{ccc} 条件型が良い &\to& この2つは対になってる \end{array}
明確に認識されることになりました。
(この時点で定義方法は2つに絞られていた)
形式的な意味での定義
これをさらに整理して厳密化したのが
\begin{array}{ccl} 外延的定義 && 中身を全て指定 \\ \\ 内包的定義 && 条件を満たすもの全て \end{array}
この「数理的な意味での定義」で
(ややこしければ列挙型条件型と呼んで良いです)
集合論に依存した話にはなりますが
(これらの定義方法は公理で定められている)
\begin{array}{ccl} 外延的定義 && \{0,1,2,3,4,5\} \\ \\ 内包的定義 && \{x \mid xは実数 \} \end{array}
これらが明確になったおかげで
私たちは『厳密な定義』を扱えるようになりました。
形式的定義が正しくなるまで
「定義の形成過程」を整理すると
\begin{array}{lcl} 非形式的定義 && 何かに対して暫定的に定義 \\ \\ 暫定的定義の修正 && 暫定的に必要な修正を \\ \\ 無矛盾の確認 && 矛盾が無いなら \mathrm{Well}\text{-}\mathrm{Defined} \\ \\ 形式的定義 && 修正済み暫定的定義が厳密な定義へ \end{array}
その手順はこんな感じになります。
(非形式的な意味での定義は超重要)
暫定的定義の段階
ここは非常に難しい段階で
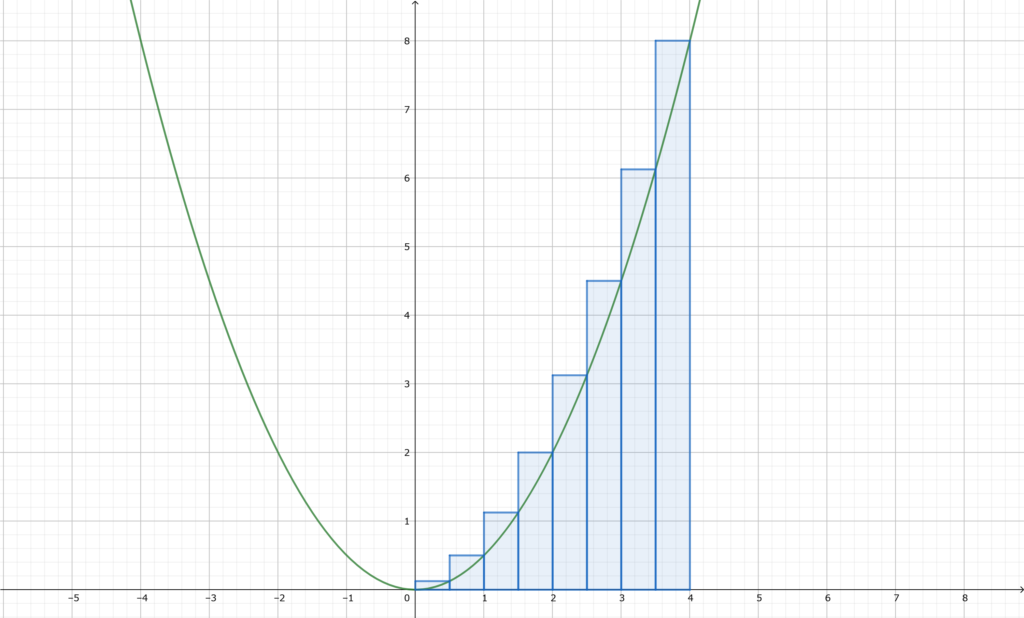
例えば「面積」について
\begin{array}{ccc} \begin{array}{lcl} \displaystyle \int_{a}^{b} f(x) \, dx &=& \displaystyle \lim_{N\to\infty}\sum_{n=1}^{N} f(x_n) \left( \frac{b-a}{N} \right) \end{array} \end{array}
「リーマン積分」を暫定的定義として採用した場合
(高校とかで習う積分のこと)
\begin{array}{ccc} 分かり易い暫定的定義 &\to& 問題無い? \end{array}
直感的には非常に理解しやすいですが
実は問題が生じます。
\mathrm{Well}\text{-}\mathrm{Defined} の段階
生じる問題の詳細は省きますが
\begin{array}{ccc} 全ての図形の面積が分かる \end{array}
例えばこのような前提を課して
\begin{array}{ccc} \begin{array}{lcl} \displaystyle \int_{a}^{b} f(x) \, dx &=& \displaystyle \lim_{N\to\infty}\sum_{n=1}^{N} f(x_n) \left( \frac{b-a}{N} \right) \end{array} \end{array}
「リーマン積分」の定義を評価した場合
\begin{array}{ccc} δ_Q (x) &=& \left\{ \begin{array}{ccc} 1 &x\in Q \\ \\ 0 & x\not\in Q \end{array} \right. \end{array}
この図形の面積を求めることができないことから
(この辺りの詳細は測度論を参照してください)
\begin{array}{ccc} 全ての図形の面積が求められる && × \end{array}
この前提に反するという結論が得られます。
(だいたいの図形は求められる)
結果
\begin{array}{ccc} 暫定的定義 &\to& 定義不十分 \end{array}
「リーマン積分」という面積の定義は
「定義不十分 \mathrm{ill}\text{-}\mathrm{defined} 」になるため
\begin{array}{ccc} 全ての図形 &\to& 単純な図形? \end{array}
「 \mathrm{Well}\text{-}\mathrm{Defined} にする」ためには
この部分を限定する必要があります。
形式的定義の段階
以上の過程を繰り返し
\begin{array}{ccc} 問題発生 &\to& 前提の整備 \end{array}
「矛盾が無くなった」と
『その時点で判断された』場合
(絶対的に矛盾しないことは保証されない)
\begin{array}{ccc} 現時点で無矛盾 &\to& \mathrm{Well}\text{-}\mathrm{Defined} \end{array}
「修正された暫定的定義(非形式)」は
「形式的定義」と呼ばれるようになります。
